绘制三次贝塞尔曲线

1. 前言

上一节我们学习了二次贝塞尔曲线，本节我们开始学习三次贝塞尔曲线。贝塞尔曲线都是由一个起点、一个终点和多个控制点组成。二次贝塞尔曲线有一个控制点，三次贝塞尔曲线有两个控制点，n 次贝塞尔曲线就有 n-1 个控制点。

2. 三次贝塞尔曲线

三次贝塞尔曲线是一种三次曲线，它可以向两个方向弯曲，由四个点来定义：两个锚点及两个控制点，控制点用来控制曲线的形状。

我们先看一下三次贝塞尔曲线的绘制过程：

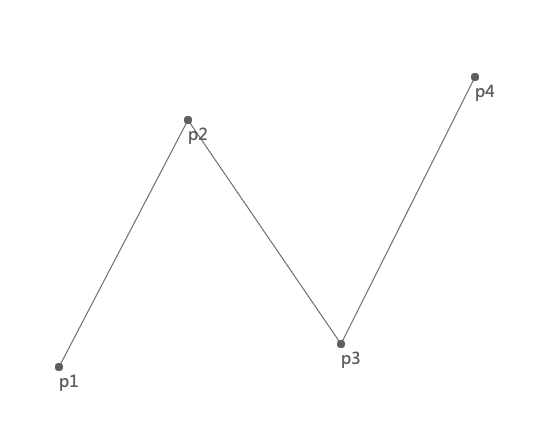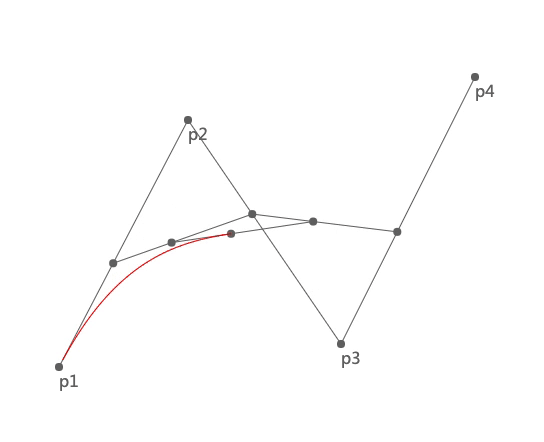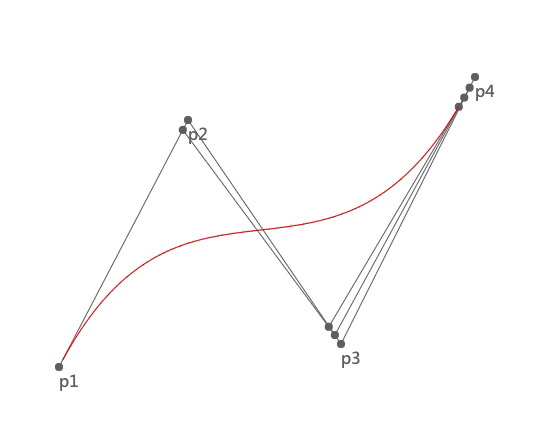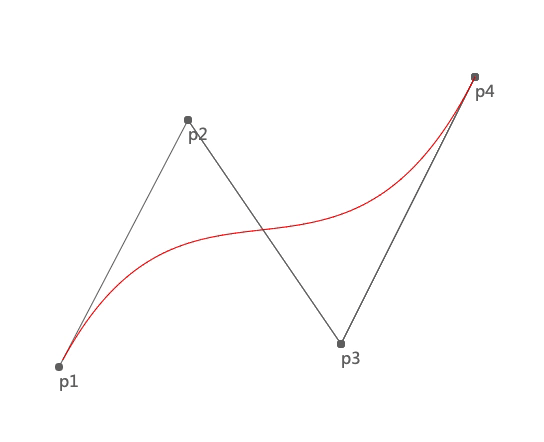
上图中 p1 和 p4 是两个锚点，p2 和 p3 是两个控制点。

在线工具

这里介绍一个开源的在线画贝塞尔曲线的工具，同学们可以体验一下：N阶贝塞尔曲线生成器

canvas 绘制三次贝塞尔曲线

在 canvas 中，绘制三次贝塞尔曲线和绘制二次贝塞尔曲线方法类似，只是比二次贝塞尔曲线多了一个控制点参数，具体绘制方法为：

ctx.bezierCurveTo(cpx1,cpy1,cpx2,cpy2,x,y);

先看整体案例：

实例演示

预览复制

<!DOCTYPE html>
<html>
<head>
	<meta charset="utf-8">
	<title>慕课网Wiki</title>
    <style>
        #imooc{
            border:1px solid #ccc;
        }
    </style>
</head>
<body>
	
	<canvas id="imooc">您的浏览器不支持 HTML5 canvas 标签</canvas>
	
	<script>
		const canvas = document.getElementById('imooc');
		canvas.width=300
		canvas.height=300
		const ctx = canvas.getContext('2d');
		
		ctx.strokeStyle="#456795";
		ctx.lineWidth=8;
		
		ctx.beginPath();
		ctx.moveTo(40,40);
		ctx.bezierCurveTo(260,150, 40,260, 160, 80);  //调用了直接绘制椭圆的函数
		ctx.stroke();
		
		//绘制起点
		ctx.beginPath();
		ctx.arc(40,40,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		//绘制控制点1
		ctx.beginPath();
		ctx.arc(260,150,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		//绘制控制点2
		ctx.beginPath();
		ctx.arc(40,260,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		
		//绘制终点
		ctx.beginPath();
		ctx.arc(160, 80,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
	</script>
</body>
</html>

<!DOCTYPE html>
<html>
<head>
	<meta charset="utf-8">
	<title>慕课网Wiki</title>
    <style>
        #imooc{
            border:1px solid #ccc;
        }
    </style>
</head>
<body>
	
	<canvas id="imooc">您的浏览器不支持 HTML5 canvas 标签</canvas>
	
	<script>
		const canvas = document.getElementById('imooc');
		canvas.width=300
		canvas.height=300
		const ctx = canvas.getContext('2d');
		
		ctx.strokeStyle="#456795";
		ctx.lineWidth=8;
		
		ctx.beginPath();
		ctx.moveTo(40,40);
		ctx.bezierCurveTo(260,150, 40,260, 160, 80);  //调用了直接绘制椭圆的函数
		ctx.stroke();
		
		//绘制起点
		ctx.beginPath();
		ctx.arc(40,40,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		//绘制控制点1
		ctx.beginPath();
		ctx.arc(260,150,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		//绘制控制点2
		ctx.beginPath();
		ctx.arc(40,260,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
		
		
		//绘制终点
		ctx.beginPath();
		ctx.arc(160, 80,8,0,2*Math.PI)
		ctx.fillStyle= "#888"
		ctx.fill()
	</script>
</body>
</html>

运行案例点击 "运行案例" 可查看在线运行效果

运行结果：

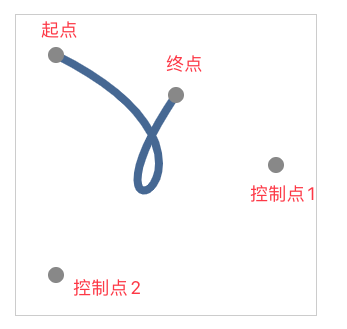
这样我们就绘制了一条三次贝塞尔曲线。

3. 方法整理

本小节中我们使用到一个新的方法 bezierCurveTo()。

3.1 bezierCurveTo() 方法

bezierCurveTo 方法作用是绘制一条三次贝塞尔曲线。

变量说明：

变量名	类型	是否必须	说明
cpx1	Number	是	控制点位置1的X坐标。
cpy1	Number	是	控制点位置1的Y坐标。
cpx2	Number	是	控制点位置2的X坐标。
cpy2	Number	是	控制点位置2的Y坐标。
x	Number	是	终点位置的X坐标。
y	Number	是	终点位置的Y坐标。

4. 总结

本小节我们主要学习了利用 bezierCurveTo 方法绘制一条三次贝塞尔曲线，这个方法有6个参数，分别是两个控制点和终点的坐标。