1. 前言
上个章节介绍了单链表反转,单链表还存在一些经典的问题,例如找到链表的倒数第 K 个节点,或者在原始链表上进行快速排序,或者是判断一个单链表是否成环,这些问题看似没有共同性,但是都可以使用快慢指针(Fast-Slow Point)方法解决。
2. 链表成环问题
面试官提问:给定一个单链表,判断链表是否存在环?能否在不使用额外空间的情况下解决问题?
题目解析:
链表成环问题是来源于算法网站LeetCode的经典题目,题目链接:https://leetcode.com/problems/linked-list-cycle/。
暴力破解方法是使用额外的数组结构,数组每一个元素存储链表的值以及节点哈希地址,在遍历链表的时候,如果发现遍历到相同哈希地址的节点,说明链表有环,否则直到遍历到链表末尾节点为止。
但是面试官要求在原始数组上操作,空间复杂度控制在O(1)。
使用单个指针则没有记忆能力,所以肯定要使用两个以上的指针遍历链表,最常用解法就是快慢指针法。
经典快慢指针的算法核心思路是:
(1)初始定义:定义一个指针 slow,每次走一个 Node 节点;定义一个指针 fast,每次走两个 Node 节点;
(2)终止条件一:当快指针走到了 Null 节点,说明链表没有成环;
(3)终止条件二:当快指针和慢指针同时走到了一个节点,说明该链表有环;
(4)附加计算一:当满足链表有环时,将慢指针重置到链表头部,然后快慢指针同时走,每次只走一个节点,当两个指针再次相遇时,相遇点即是链表的环入口;
(5)附加计算二:当满足链表有环时,停止快指针,每次慢指针走一个 Node 节点,当两个节点再次相遇时,慢指针重新走的长度即是链表长度。
最重要的环节在于如何证明慢指针和快指针会在环中相遇,我们假设一个通用的有环链表如下图所示:
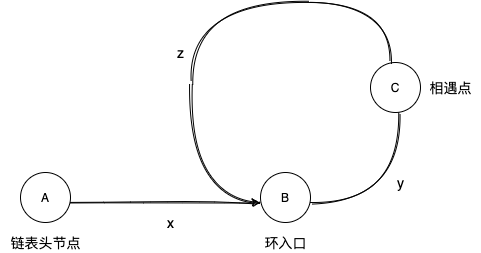
其中A—>B 的距离为 x,B—>C 的距离为y,C—>B 的距离为 z。
假设慢指针走了a步,那么快指针走了2a步,因为相遇时快指针已经在环上循环了n次,所以满足公式:
2*(x+y) = x+y+n*(y+z),所以x+y = n * (y+z)。快慢指针之间的距离会逐渐增大,结果是要么快指针提前走到了链表末尾,要么是快指针刚好多走出n个链表长度,说明链表有环。
我们在白板上可以写出算法实现,示例:
public class Solution {
public boolean hasCycle(ListNode head) {
//如果链表为空或者只有一个节点,肯定不成环
if(head==null || head.next==null){
return false;
}
ListNode slow = head;
head=head.next;
while(head!=null && head.next!=null){
//当快慢指针相遇,说明链表有环
if(slow==head){
return true;
}
slow=slow.next;
head=head.next.next;
}
return false;
}
}
算法的时间复杂度为O(N),其中N表示链表长度,空间复杂度为O(1),因为没有使用额外辅助空间。
3. 小结
本章节介绍了最基础的快慢指针算法,快慢指针是解决链表问题的银弹。例如找到链表的倒数 K 个节点,也可以另快慢指针间距为 K,两者步长相同,最终慢指针走到的节点即是目标节点。对于快慢指针用法,候选人需要注意两点: ① 边界条件:如果是空链表或者单节点链表,直接使用快慢指针可能会导致空指针异常,需要特殊处理; ② 快慢指针不一定是步长相差两倍,可能是步长相同,但是一个走在前,一个走在后。