-

- 慕斯8442767 2020-11-05
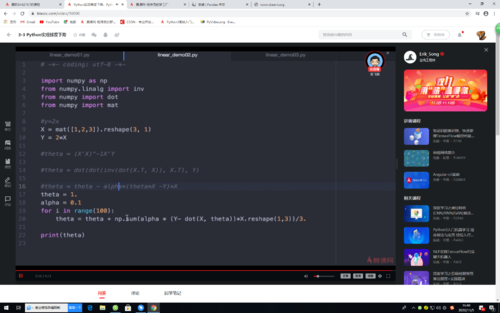
梯度下降法计算
- 0赞 · 0采集
-

- 霜花似雪 2019-10-26
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
import numpy as np from numpy.linalg import inv from numpy import dot from numpy import mat if __name__ == "__main__": # 训练数据 x = mat([1, 2, 3]).reshape(3, 1) # 1行3列转化为3行1列 y = 2 * x #梯度下降: # 原理:多次更新theta的值,通过theta与x,y的关系来得到theta # theta = theta - alpha*(theta*x-y)*x (alpha取值为0到1,保证梯度下降的变化速率不要太快,在一个合适的区间之内,使得函数迅速收敛,找到局部最小值) theta = 1.0 #初始化theta alpha = 0.1 #初始化alpha for i in range(100): theta = theta + np.sum(alpha * (y - dot(x, theta)) * x.reshape(1, 3))/3 # np.sum 求加权平均值 print(theta)
- 0赞 · 0采集
-

- 滕玉龙 2018-12-06
掌握python梯度下降求解线性分析模型参数
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
>>> import numpy as np
>>> from numpy.linalg import inv
>>> from numpy import dot
>>> from numpy import mat
>>> X=mat([1,2,3]).reshape(3,1)
>>> Y=2*X
>>> theta=1.0
>>> alpha=0.1
>>> for i in range(100):
... theta=theta + np.sum(alpha*(Y-dot(X,theta))*X.reshape(1,3))/3.0
...
>>> print(theta)
2.0
>>>
- 0赞 · 1采集
-

- 程序小工 2018-08-23
梯度下降的实现
-
截图0赞 · 0采集
-

- 明天也爱你 2018-07-23
掌握python梯度下降求解线性分析模型参数
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
>>> import numpy as np
>>> from numpy.linalg import inv
>>> from numpy import dot
>>> from numpy import mat
>>> X=mat([1,2,3]).reshape(3,1)
>>> Y=2*X
>>> theta=1.0
>>> alpha=0.1
>>> for i in range(100):
... theta=theta + np.sum(alpha*(Y-dot(X,theta))*X.reshape(1,3))/3.0
...
>>> print(theta)
2.0
>>>
- 0赞 · 0采集
-

- binobigo 2018-05-31
用梯度下降算法来实现:
1、梯度下降算法方程:theta = theta - alpha*(theta*X - Y)*X
2、程序实现:
alpha = 0.1
theta = 1.0
for i in range(100):
theta = theta + np.sum(alpha * (Y - dot(X, theta)) * X.reshape(1, 3))/3
-
截图0赞 · 0采集
-

- Alphabc 2018-05-12
梯度下降
-
截图0赞 · 0采集






