左侧为正向传播过程，右侧为调校参数过程

训练的过程，正向传播与反向传播

神经网络训练过程

对bp神经网络的多轮单个样本更新权重和阈值的迭代代码实现，参考吴恩达机器学习
  def loss(self,x,y,lamba=0.01):        
      n_train,n_features=x.shape       
       #前向传播        
      mulIToH=sigmoid(np.dot(x,self.weightIToH_)+self.b1)#隐藏层输出结果n_train*self.wHN_       
      mulHToO=sigmoid(np.dot(mulIToH,self.weightHToO_)+self.b2)#输出层输出结果n_train*self.oN_       
      loss=-np.sum(y*np.log(mulHToO)+(1-y)*np.log(1-mulHToO))/n_train     
      loss+=0.5*lamba*(np.sum(self.weightIToH_*self.weightIToH_)+np.sum(self.weightHToO_*self.weightHToO_))/n_train      
      #backward后向传播过程      
      errorOut=mulHToO-y#n_train*self.oN_     
      dWeightHToO=np.dot(mulIToH.T,errorOut)+lamba*self.weightHToO_        
      db2=np.sum(errorOut,axis=0)        
      for temp in range(mulIToH.shape[1]):            
          mulIToH.T[temp]=derivativeOfSigmoid(mulIToH.T[temp])        
      errorHidden=np.dot(errorOut,self.weightHToO_.T)*mulIToH.T        
      dWeightIToH=np.dot(x.T,errorHidden)+lamba*self.weightIToH_        
      db1=np.sum(errorHidden,axis=0)       
      dWeightHToO/=n_train       
      dWeightIToH/=n_train     
      db2/=n_train      
      db1/=n_train   
     return loss,dWeightIToH,dWeightHToO,db1,db2

讲解这个训练过程，以及网络向量化（正向传播）、网络梯度下降（网络反向传播），是为了我们在使用框架时（使用现成的神经网络算法时），明白神经网络的执行机制。

因此，老师没有讲解例子，自己来编写这些代码。

可能后续会有课程，使用这些框架。

比如：老师的另一门免费课：

使用python实现线性回归？

实际上，我在写程序的时候，没有使用损失函数，LOST的计算，直接使用

y' - y （y'是网络模拟出输出，y为原始数据）来判断网络误差。

迭代，调整参数

左边利用输入值通过每一层网络的结构计算出下一层输出

直到结束，计算出损失

右边通过损失函数不断更新W，b,知道计算出最小的损失函数

观察神经网络过程形成较为直观的理解

梯度下降逆向更新W,b

一边正向一边逆向，重复这个流程

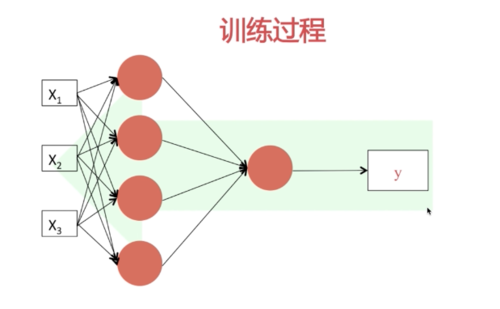
训练过程

左边成为正向传播

通过输入值按照每一层网络的结构计算出下一层的输出

直到结束，结束的时候计算出整个网络的损失

右侧是一个参数(W,b)调校的过程

通常会用到左边的W，b参数，而这些参数通常是会缓存的，这样会提高我们的运算效率（z^n,W^n,b^n）

实际上是逐步更新参数的过程

然后用新的参数载重复上面的过程

知道我们的损失函数趋向于一个最小值

参数全部算好然后一次性更新

訓練過程:

训练过程的两部分