为什么使用堆(数据结构)
堆的一个概念 就是优先队列;

优先队列有两个操作,入队,出队(取出优先级最高的元素)

堆的基本实现
1.二叉堆 Binary Heap
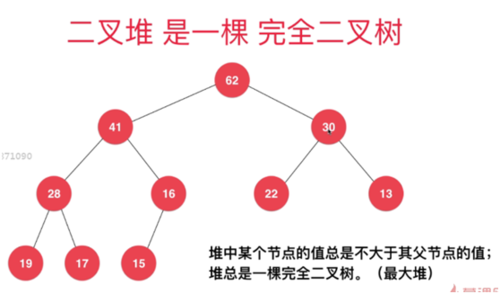
特点:1,任何一个节点不大于父亲节点
2,是一颗完全二叉数,就是除了最后一层节点外,其他层节点数必须是最大值,最后一层的所有节点几种在最左侧--------就叫完全二叉树
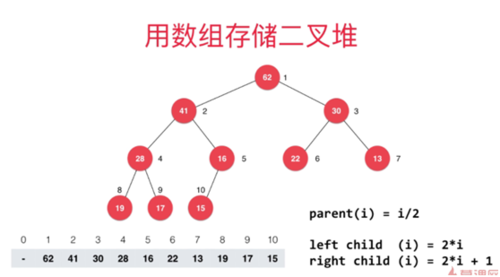
堆的经典实现方式:使用数组来存储一个二叉堆,左节一次放大2倍,右节点则是2倍加1
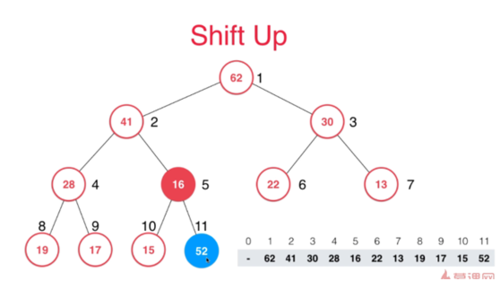
Shift Up
如何添加元素:我们需要做的是,将新加入元素调整到合适位置,使得整个二叉树依然保持最大堆的性质。 首先我们需要比较新加入元素和父节点比,16比52小违背了最大堆定义,所以交换位置,在和父节点比,41小于52 所以在交换位置,在和父节点比,52小于62,此时可以不用动了。
代码:
public class MaxHeap {
private Integer[] item;
private int count;
public MaxHeap(int capacity){
this.item=new Integer[capacity+1];
}
public int size(){
return count;
}
public Boolean isEmpty(){
return count==0;
}
void insert(int data) {
item[count+1]=data;//首先给新添加元素一个为位置
count++;
//新加入元素有可能破坏了对的定义,所以我们需要shifUP比较
shipUp(count);
}
private void shipUp(int k){
//我们每一次看k这个位置与父节点(k/2)比较
while (k>1&&item[k/2]<item[k]){
SortTestHelper.swap(item,k/2,k);
k/=2;
}
}
}
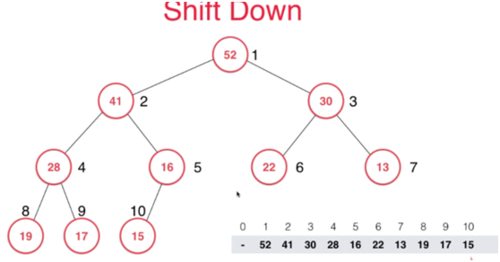
Shift Down
思想:首先优先队列取出数据应该是根节点元素,这样就少了一个元素,之后我们去最后一个节点放到根节点上,响应的count 应该减一,这样所以为11的元素可以不动,我们一count为节,就不会访问到16这个元素,但此时不符合完全二叉树,下面调整位置,来满足完全二叉树定义,我们将16向下比较,首先左右两个孩子比较,谁大就和谁交换为位置,之后继续下移.

private void shiftDown(int k){
while (2*k<=count){//在一颗完全二叉树种,有左孩子,我们就说他有孩子。
int j=2*k;//在此轮循环中,data[k]和data[j]交换位置;
if (j+1<=count&&item[j+1]>item[j]){
j+=1;
}
if(item[k]>=item[j]){
break;
}
SortTestHelper.swap(item,k,j);
k=j;
}
}
基础堆排序和Heapify
版本一的堆排序算法:
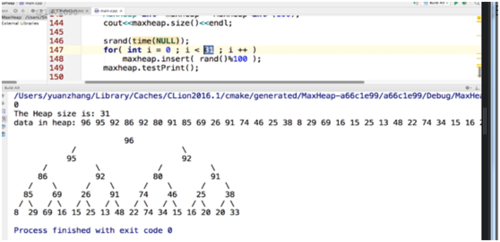
我们利用堆实现第一个排序算法,首先将数组arr中的元素全部加入到堆中,maxHeap.insert(arr[i]),之后我们再从堆中将数一个一个取出来就是从大到小的顺序,想要从小到大的顺序,就反正去出来就可以了。
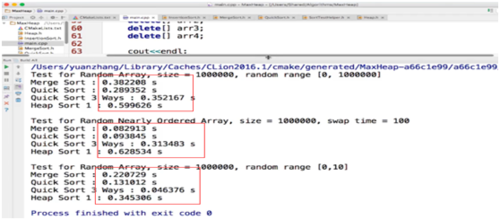
下面是测试结果,看结果堆排序,相对于快排和归并来书说稍慢,但是还是在一个数量级内的,堆排序本身也是一个n*longN的排序。
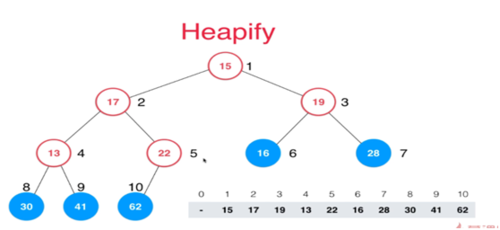
Heapify
就是给定一个数组并且让数组形成堆形状,我们称之为Heapify。
如下图,我们拿到一个数组,就可以直接转化成二叉数,当然,这样的二叉树不符合我完全二叉树的定义,下面有两个属性;
属性一:所有叶子节点(就是没有孩子的节点,本身就一个元素,本身符合完全二叉树)可以不用考虑。
属性er:第一个父节点是数组长度除以2的得到了。
我们可以从第一个父节点入手用执行shift down操作就可以了。
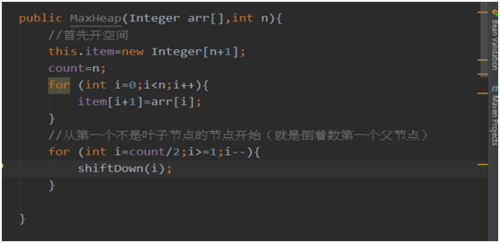
我们利用新的Heapify得构造函数,实现排序算法

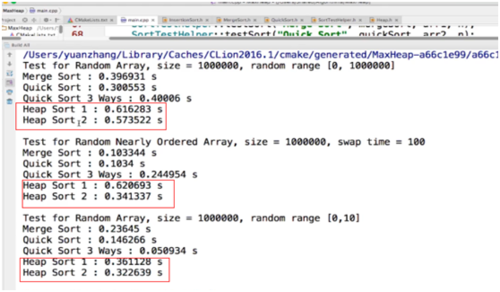
下图为测试结果:
第二个堆排序性能优第一个对排序,但还是没有前两个算法好,所以系统级别的算法一般不用堆排序,堆这种数据结构,跟多是对动态数据的维护。

6优化的堆排序
原地堆排序思想:
实际上 一个数组就可以看成一个堆,可以通过heapify的过程,将数组编程最大堆,最大的是数组第一个位置,如果从小到大排序,我么需要将数组,第一位置与最后一个位置交换,之后除了最后一个位置的部分 就不是最大堆了。此时我们需要对w这个位置坐shifdown操作,从而将整个数组再次变为最大堆,循环即可。

由于用原数组直接排序,所以索引从0开始,索引如下图:
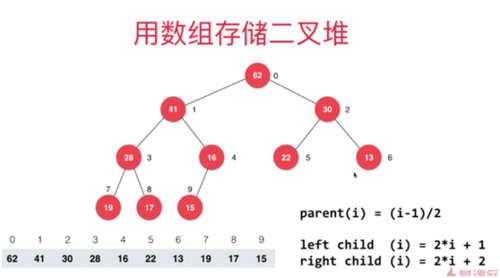
第一个非页子节点索引,如下图;
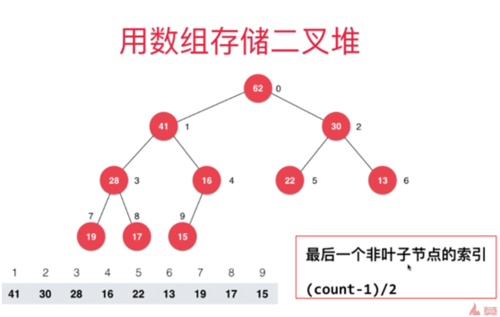
首先我们从第一个非页子节点位置开始循环 heapify过程,将数组构建成一个最大堆,
之后需要做前面所说的位置交换操作,交换后,在对剩下部分做shiftdown操作,注意从0开始索引


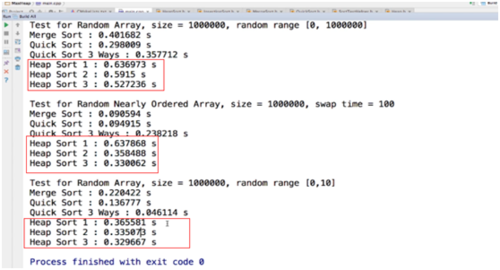
看运行结果:比前两个要快,因为不要开开辟额外的空间进行处理,所以开辟新空间包括往新空间里复制都省了

 随时随地看视频
随时随地看视频




