分析二分查找法和斐波那契数列的时间和空间复杂度

接上篇算法的时间复杂度与空间复杂度分析，传送门：算法的时间复杂度与空间复杂度分析

下面以二分查找法和斐波那契数列分析其时间和空间复杂度：

1.二分查找法的时间复杂度

#include <stdio.h>  int searchItem(int arr[],int len, int value){  
    int low = 0,high = len-1,mid;  
    while (low <= high) {  
        mid = (low + high)/2;  
        if (value > arr[mid]) {  
            low = mid+1;  
        }else if (value < arr[mid]){  
            high = mid - 1;  
        }else{  
            return mid;  
        }  
    }  
    return -1;  
}  

int main(int argc, const char * argv[]) {  
   int a[10] = {15,17,18,22,35,51,60,88,93};  
    int l = searchItem(a,22,9);  
    printf("loc = %d\n",l);  
    return 0;  
}  12345678910111213141516171819202122

注意：其一定是已排序数组
数组中间位置的元素值Kmid

• 如果Kmid=k，那么检索工作完成

• 当Kmid>K，在前半部分检索

• 相反，在后半部分检索

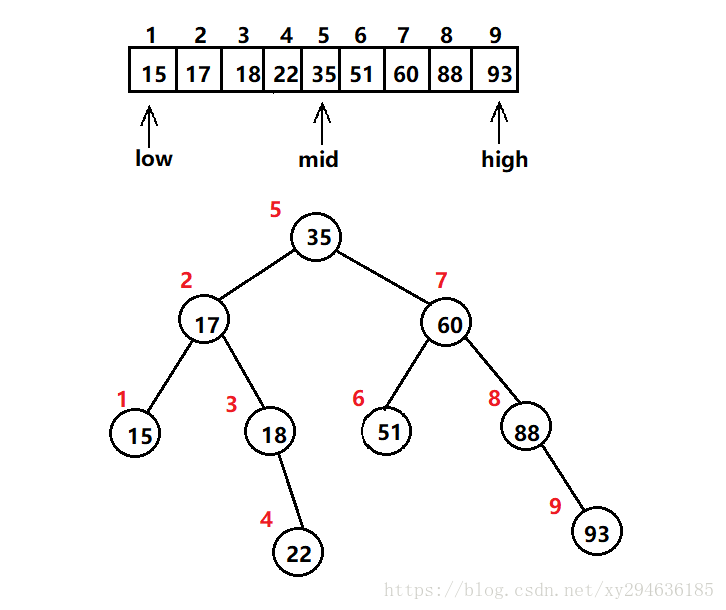
首先了解二分查找，首先在长度为n的表范围中查找，第一次循环在n/2中查找，第二次在n/2/2中查找，依次循环。假设在第X次找到，那么 就是找2的X次方次，有2的X次方=n解出x为log2的n ，故时间复杂度为log2N。由于辅助空间是常数级别的所以空间复杂度是O(1);

最大检索长度：
[log2(n+1)]
平均检索代价：
O(log n)
在算法复杂性分析中

• log n是以2为底的对数

• 以其他数值为底，算法量级不变

2.斐波那契数列的时间和空间复杂度

int fibona_recur(int n){  
    if(n<2){  
        return n;  
    }  
    else{  
        return fibona_recur(n-1)+fibona_recur(n-2);  
    }  
}   
//时间复杂度：O(2^n) 空间复杂度为：O(1);  
int main(){  
    int i=0;  
    for(i;i<12;i++){  
    int m=fibona_tail_recur(i,0,1);  
    printf("%d ",m);          
    }  
    return 0;  
}  1234567891011121314151617

以5为例：

将递归执行图画出来可以明显的看出来，这是一颗二叉树，无论他是否是满二叉树，因为我们前面说过我们只计算最坏的情况，所以要计算这课二叉树有多少个元素，数的深度为n，那么元素为2^N-1；去掉常数项就是2的n次方

递归的时间复杂度是：  递归次数*每次递归中执行基本操作的次数
所以时间复杂度是： O(2^N)  
递归的空间复杂度是：  递归的深度*每次递归所需的辅助空间的个数
所以空间复杂度是：O(N)

原文出处