像素层面上,CNN能做的,自注意力(self-attention)也都能做。
统御NLP界的注意力机制,不仅被迁移到了计算机视觉中,最新的研究还证明了:
CNN卷积层可抽取的特征,自注意力层同样可以。

△论文地址:https://arxiv.org/abs/1911.03584
这项工作来自洛桑理工学院,研究表明:
只要有足够的头(head)和使用相对位置编码,自注意力可以表达任何CNN卷积滤波层。
此外,还中选ICLR 2020,在Twitter上也受到了广泛的关注。
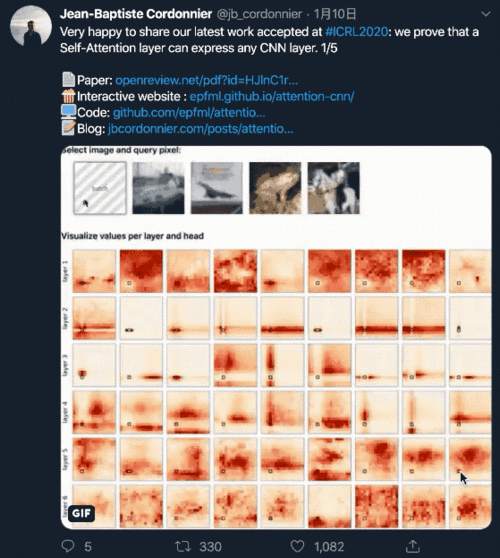
在论文摘要末尾,作者还霸气的附上了一句:

代码已开源!
多头自注意力层如何表达卷积层?
众所周知,Transformer的兴起,对NLP的发展起到了很大的作用。
它与以往的方法,如RNN和CNN的主要区别在于,Tranformer可以同时处理输入序列中的每个单词。
其中的关键,就是注意力机制。
尤其是在自注意力情况下,可以无视单词间的距离,直接计算依赖关系,从而学习一个句子中的内部结构。
那么,问题来了:自注意力能替代CNN吗?
为了研究这个问题,需要先来回顾一下它们分别是如何处理一张图像。
给定一张图像,其大小为W x H x D。
卷积层
卷积神经网络由多个卷积层和子采样层组成。
每个卷积层可以学习大小为K x K的卷积滤波器,输入和输出的维度分别是Din和Dout。
用一个4D核张量(维度为K x K x Din x Dout)和一个偏置向量b(维度为Dout)来对层进行参数化。
下面这张动图便展示了如何计算q的输出值。
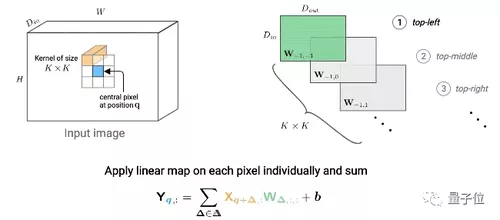
△对于个K x K的卷积,计算给定像素(蓝色)的输出值。
多头自注意力层
CNN和自注意力层的主要区别是,一个像素的新值依赖于图像的其他像素。
相对于感受野(receptive field)是K x K领域网格的卷积层,自注意力的感受野始终是全图像。
这就带来了一些“缩放”方面的挑战。
自注意力层由一个大小为Dk的键/查询,大小为Dh的头,一组头Nh,以及一个维度为Dout的输出组成。
对于每个头h,由一个键矩阵(key matrix)W(h)key,查询矩阵(query matrix)W(h)qry和一个值矩阵(value matrix)W(h)val来进行参数化。
映射矩阵Wout用来将所有头集合到一起。
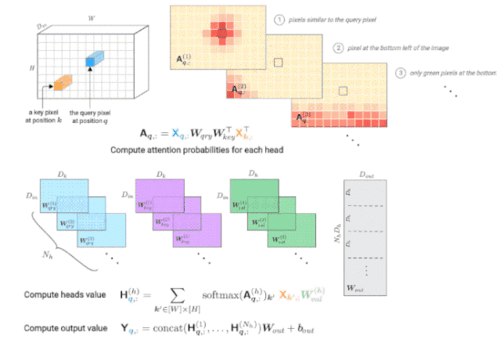
△由多头自注意力层计算查询像素(深蓝色)的输出值。右上角显示每个头的注意力概率示例,红色位置表示“注意力中心”。
再参数化
到这一步,你可能已经观察到了自注意力层和卷积层之间的相似性。
假设每对键 / 查询矩阵(W(h)key和W(h)qry)可以在任意shift△处专注于单个像素。
然后每个注意力头将学习一个值矩阵W(h)val。
因此,卷积核的感受野中像素个数与头(Nh=K x K)的个数相关。
也就是说,使用一个多头注意力层就能模拟一个卷积层。
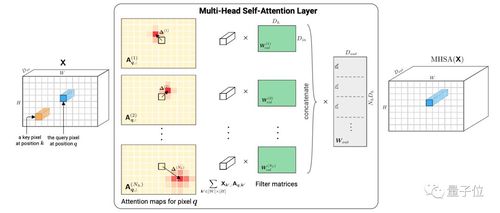
△将一个多头自注意力层应用于张量图像X。
用自注意力层表达卷积层时,有2个关键的要求:
多个头去处理卷积层感受野的每个像素:例如3 x 3的核需要9个头
使用相对位置编码来确保平移等变性(translation equivariance)
相对位置编码
自注意力模型的一个关键特性,是它的输出与输入像素的打乱方式无关。
在输入顺序比较重要的情况下,这会导致一些问题。
为了减轻这种限制,对序列中的每个标记(或图像中的像素)进行位置编码,并在应用自注意力机制之前将其添加到标记本身的表示中。
根据输入值和层输入的位置编码计算注意力概率:

可以看到,对于每个查询像素,每个头部都可以专注于图像的不同部分(位置或内容)。
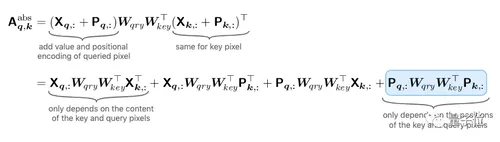
由于卷积层的感受野不依赖于输入数据,所以只需要上面式子中的最后一项,就可以用自注意力来模拟CNN的表现。
而要实现CNN的平移等变性(equivariance to translation),可以通过用相对位置编码替代绝对位置编码的方式来实现。
学习注意力模式(Learned Attention Patterns)
那么,用自注意力层来表达卷积层,在实际当中能发挥什么样的作用?
研究人员设计了一个6层的全注意力模型,每层有9个头。
在CIFAR-10上训练这一模型,使其完成监督分类任务。模型达到了94%的准确率。
并且,研究人员用相对位置编码,分别学习了行偏移和列偏移编码。相对位置编码仅设定注意力概率,而非输入值。
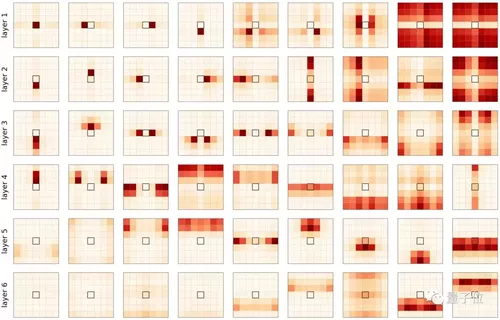
上面这张图,是每个层(行)上的每个头(列)的注意力映射。中间的黑色方块是查询像素。
注意力概率表明,自注意力的行为与卷积是相似的。每个头都学会了聚焦图像的不同部分。
另外还可以观察到,第一层(1-3)专注于非常接近的和特定的像素,而较深层(4-6)专注于图像整个区域像素的更多全局斑块。

ICLR 2020获评“6-6-6”
这篇论文已经被ICLR 2020接收,评审们给出了3个6分。
一位评审在review中写道:
这篇论文从理论上证明了多头自注意力层可以表示卷积滤波器。
相当关键的是其中使用了自注意力层的相对位置编码。论文中称,这一结果可以扩展到其他形式的位置编码。
不过有一点需要注意,看起来,注意力层的权重需要任意大才能准确表示卷积层。
总的来说,我认为本文朝着了解注意力和卷积层之间的异同迈出了坚实的一步。
另一位评审表示,二次相对编码的推到是一个很好的理论构造。不过,由于作者仅在CIFAR上进行了实验,其贡献还不足以建立新的相对注意力机制。
对于这一研究,网友们也纷纷点赞。
谷歌大脑研究科学家David Ha评论道,对于图像和序列处理,自注意力是很好的统一先验。还可以用于学习对卷积层而言难以学习的图像。
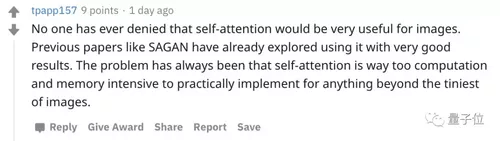
不过,也有网友提出了质疑:
自注意力需要耗费大量计算和内存,实际上无法在最小图像之外的任何东西上实现。
代码已开源,实验可复现
正如论文摘要最后一句:
Our code is publicly available.
这项工作的代码已经在GitHub上开源。
注意的是,需要在有GPU的Ubantu上运行代码,而且要在新的Anaconda环境中安装一个Python包:
conda install pytorch torchvision cudatoolkit=10.0 -c pytorch
pip install -r requirements.txt
通过运行 run/ 文件夹里的代码,论文中的所有实验都可以复现,例如:
bash runs/quadratic/run.sh
最后,介绍一下论文作者。
论文一作,是正在瑞士洛桑联邦理工学院(EPFL)攻读博士的Jean-Baptiste Cordonnier。

他致力于无监督知识提取、图神经网络、自然语言处理和分布式优化的研究。研究成果已登上NeurIPS 2018、IJCAI 2019、ICLR2020等顶会。

 随时随地看视频
随时随地看视频




