文章目录
从本次开始,我们将开启新的篇章:深度学习系列。主要涉及三个部分,一是,深度学习基础:包括深度学习历史及基本概念,感知机,BP神经网络,神经网络等初步介绍;过程中会引入一些基础概念:反向传播,随机梯度下降,学习率衰减,损失函数等;二是,深度学习典型算法第一部分:包括深度神经网络DNN、卷积神经网络CNN、深度置信网络DBN等;三是,深度学习典型算法第二部分:包括递归神经网络RNN,循环神经网络RNN,生成对抗式网络GAN等。本次只介绍第一部分,深度学习基础。
赫伯特·西蒙教授(Herbert Simon,1975年图灵奖获得者、1978年诺贝尔经济学奖获得者)曾对“学习”给了一个定义:“如果一个系统,能够通过执行某个过程,就此改进了它的性能,那么这个过程就是学习”。学习的核心目的,就是改善性能。
那机器学习又是什么呢?不知道大家还记不记得,在该系列教程开篇我们提到过这个问题: 机器学习本质是什么? 我们当时是这么说的:
机器学习 ≈≈ 寻找一个函数/数学
如下图所示,常用的语音识别、图像识别、对话系统等,训练模型的过程都是在寻找一个任务相关的最优化函数。

也就是说,需要找到一个关于输入输出的映射关系,也就是一个最优化函数,那如何确定这样一个最优化的函数呢?
形象的说,为了确定最优化映射关系(函数),会生成一系列的函数,这就是模型的训练过程,再从中选取最优的函数,如上图所示,f_1f1就优于f_2f2,因为f_1f1能准确识别图片,而f_2f2不能。
今天的主角登场!深度学习又是什么?它和机器学习又是啥关系?这在第一堂课中其实也提及了。
简要回顾一下:
一位微软工程师对它们的解释

What?借用网上一句话,不要慌,看不懂的一律当作约饭机器学习处理。
言归正传,本着不以说清楚为目的的教程都是耍流氓的精神:
人工智能:计算机领域类的一套概念。
机器学习:一种实现人工智能的方法。
深度学习:一种实现机器学习的技术。
今天我们从另一个角度来进行解释,因为之前我们已经讲过了统计的相关课程,今天从统计的角度进行解释:学习的四个象限
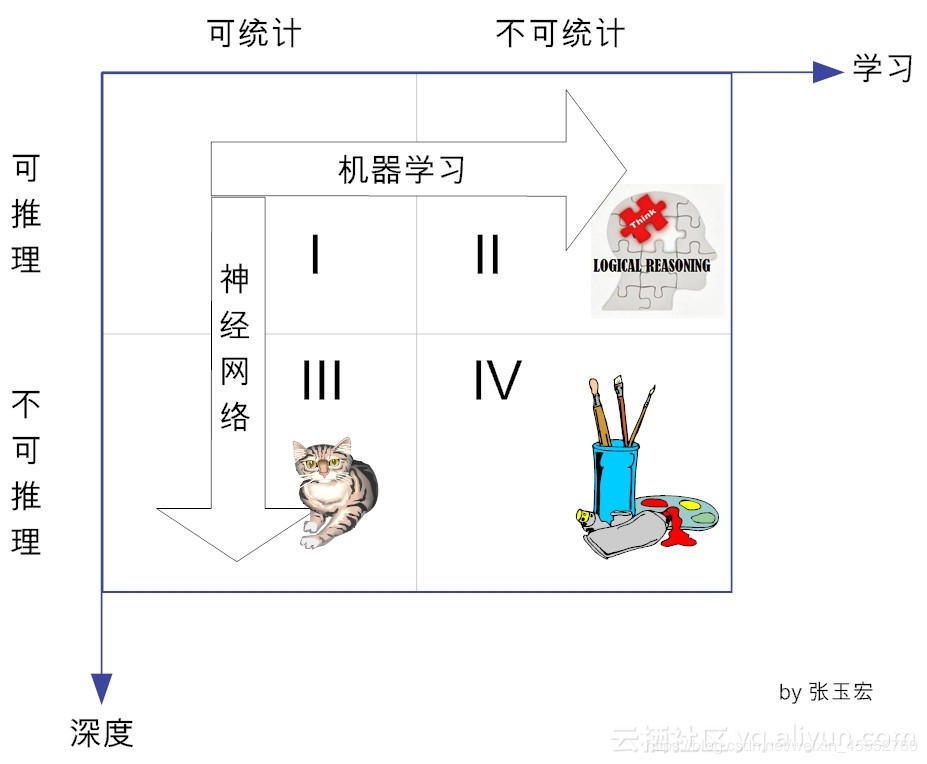
怎么理解呢?
由「可推理可统计」向「可推理不可统计」发展部分的手段为机器学习,由「可推理可统计」向「不可推理可统计」法阵的手段为深度学习,而深度学习用到了神经网络的理论。两个学习都是人工智能的范围。那第IV象限是什么鬼? 那属于强学习范畴了,目前我们狭义上的弱机器学习是搞不定的。
当遇到一个陌生对手的时候,如何以最佳方式干翻tata?最好入手的地方当然是深扒tata的过去,只有了解tata的过去,把握历史,才能抓住现在与未来!
1943年
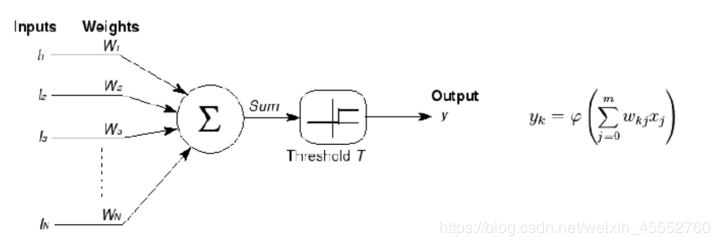
由神经科学家麦卡洛克(W.S.McCillochW.S.McCilloch) 和数学家皮兹(W.PittsW.Pitts)在《数学生物物理学公告》上发表论文《神经活动中内在思想的逻辑演算》(A Logical Calculus of the Ideas Immanent in Nervous ActivityALogicalCalculusoftheIdeasImmanentinNervousActivity)。建立了神经网络和数学模型,称为MCPMCP模型。所谓MCPMCP模型,其实是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型,也就诞生了所谓的“模拟大脑”,人工神经网络的大门由此开启。MCPMCP当时是希望能够用计算机来模拟人的神经元反应的过程,该模型将神经元简化为了三个过程:输入信号线性加权,求和,非线性激活(阈值法)。如下图所示
1958年
计算机科学家罗森布拉特(RosenblattRosenblatt)提出了两层神经元组成的神经网络,称之为“感知器”(PerceptronsPerceptrons)。第一次将MCPMCP用于机器学习分类。**“感知器”**算法算法使用MCPMCP模型对输入的多维数据进行二分类,且能够使用梯度下降法从训练样本中自动学习更新权值。1962年,该方法被证明为能够收敛,理论与实践效果引起第一次神经网络的浪潮。
1969年
纵观科学发展史,无疑都是充满曲折的,深度学习也毫不例外。 1969年,美国数学家及人工智能先驱Marvin MinskyMarvinMinsky在其著作中证明了感知器本质上是一种线性模型(linear modellinearmodel),只能处理线性分类问题,就连最简单的XORXOR(亦或)问题都无法正确分类。这等于直接宣判了感知器的死刑,神经网络的研究也陷入了将近20年的停滞。
1986年
由神经网络之父Geoffrey HintonGeoffreyHinton在1986年发明了适用于多层感知器(MLPMLP)的BP(Backpropagation)BP(Backpropagation)算法,并采用SigmoidSigmoid进行非线性映射,有效解决了非线性分类和学习的问题。该方法引起了神经网络的第二次热潮。
注:SigmoidSigmoid函数是一个在生物学中常见的SS型的函数,也称为SS型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,SigmoidSigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间。
90年代时期
1991年BPBP算法被指出存在梯度消失问题,也就是说在误差梯度后项传递的过程中,后层梯度以乘性方式叠加到前层,由于SigmoidSigmoid函数的饱和特性,后层梯度本来就小,误差梯度传到前层时几乎为0,因此无法对前层进行有效的学习,该问题直接阻碍了深度学习的进一步发展。
此外90年代中期,支持向量机算法诞生(SVMSVM算法)等各种浅层机器学习模型被提出,SVMSVM也是一种有监督的学习模型,应用于模式识别,分类以及回归分析等。支持向量机以统计学为基础,和神经网络有明显的差异,支持向量机等算法的提出再次阻碍了深度学习的发展。
发展期 2006年 - 2012年
2006年,加拿大多伦多大学教授、机器学习领域泰斗、神经网络之父——Geoffrey HintonGeoffreyHinton和他的学生Ruslan SalakhutdinovRuslanSalakhutdinov在顶尖学术刊物《科学》上发表了一篇文章,该文章提出了深层网络训练中梯度消失问题的解决方案:无监督预训练对权值进行初始化++有监督训练微调。斯坦福大学、纽约大学、加拿大蒙特利尔大学等成为研究深度学习的重镇,至此开启了深度学习在学术界和工业界的浪潮。
2011年,ReLUReLU激活函数被提出,该激活函数能够有效的抑制梯度消失问题。2011年以来,微软首次将DLDL应用在语音识别上,取得了重大突破。微软研究院和GoogleGoogle的语音识别研究人员先后采用**深度神经网络(DNN)(DNN)**技术降低语音识别错误率20%~30%,是语音识别领域十多年来最大的突破性进展。2012年,DNNDNN技术在图像识别领域取得惊人的效果,在ImageNetImageNet评测上将错误率从26%降低到15%。在这一年,DNNDNN还被应用于制药公司的DrugeActivityDrugeActivity预测问题,并获得世界最好成绩。
爆发期 2012 - 至今
2012年,HintonHinton课题组为了证明深度学习的潜力,首次参加ImageNetImageNet图像识别比赛,其通过构建的卷积神经网络(CNNCNN)网络AlexNetAlexNet一举夺得冠军,且碾压第二名(SVMSVM方法)的分类性能。也正是由于该比赛,CNN吸引到了众多研究者的注意。
AlexNetAlexNet的创新点在于:
(1)首次采用ReLUReLU激活函数,极大增大收敛速度且从根本上解决了梯度消失问题。
(2)由于ReLUReLU方法可以很好抑制梯度消失问题,AlexNetAlexNet抛弃了“预训练++微调”的方法,完全采用有监督训练。也正因为如此,DLDL的主流学习方法也因此变为了纯粹的有监督学习。
(3)扩展了LeNet5LeNet5结构,添加DropoutDropout层减小过拟合,LRNLRN层增强泛化能力/减小过拟合。
(4)第一次使用GPUGPU加速模型计算。
2013、2014、2015、2016年,通过ImageNetImageNet图像识别比赛,DLDL的网络结构,训练方法,GPUGPU硬件的不断进步,促使其在其他领域也在不断的征服战场。
深度学习经过半个多世纪的发展,现在已经广泛应用到我们日常生活中,今天我们将从基础的开始,沿着感知机->神经网络->深度神经网络逐次介绍, 并在介绍的过程中引入一些深度学习里的基础概念:反向传播,随机梯度下降,学习率衰减,损失函数等。
如果大家有印象的话,我们在概率统计机器学习时,简单介绍过感知机。它是一个二分类的线性模型,结构如下图所示,
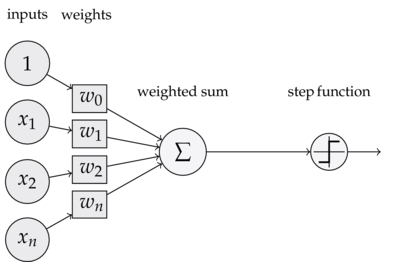
可以看到,一个感知器有如下组成部分:
输入权值 一个感知器可以接收多个输入(x_1,x_2,\dots,x_n|x_i\in R)(x1,x2,…,xn∣xi∈R),每个输入上有一个权值w_i\in Rwi∈R,此外还有一个偏置项b\in Rb∈R,就是上图中的w_0w0。
激活函数 感知器的激活函数可以有很多选择,比如我们可以选择下面这个 阶跃函数ff 来作为激活函数:
f(z)= \begin{cases} \begin{aligned} 1 && z > 0\ 0 && otherwise\ \end{aligned} \end{cases}f(z)={10z>0otherwise
先不用管激活函数这个概念,现只需知道是将线性转为非线性表达即可。
输出 感知器的输出由下面这个公式来计算
y=f(w*x+b)y=f(w∗x+b)
如果看完上面的公式一下子就晕了,不要紧,我们用一个简单的例子来帮助理解。
例子:用感知器实现andand函数
我们设计一个感知器,让它来实现andand运算。andand是一个二元函数(带有两个参数x_1x1和x_2x2),下面是它的真值表:
x_1x1x_2x2yy
000
010
100
111
为了计算方便,我们用00表示falsefalse,用11表示truetrue。
我们令w_1=0.5,w_2=0.5,b=-0.8w1=0.5,w2=0.5,b=−0.8,(真实场景是训练得到),而激活函数就是前面写出来的阶跃函数,这时,感知器就相当于and函数。不明白?我们验算一下:
输入上面真值表的第一行,即x_1=0,x_2=0x1=0,x2=0,那么根据公式(1),计算输出:
\begin{aligned}y &=f(xx+b) \ &=f(w_1x_1+w_2x_2+b)\ &=f(0.50+0.5*0-0.8)\&=f(-0.8)\ &=0 \end{aligned}y=f(x∗x+b)=f(w1x1+w2x2+b)=f(0.5∗0+0.5∗0−0.8)=f(−0.8)=0
也就是当x_1,x_2x1,x2都为00的时候,yy为00,这就是真值表的第一行。大家可以自行验证上述真值表的第二、三、四行。同理,感知机还能实现oror函数。
感知机还能做点什么?
事实上,感知器不仅仅能实现简单的布尔运算。它可以拟合任何的线性函数,任何线性分类或线性回归问题都可以用感知器来解决。前面的布尔运算可以看作是二分类问题,即给定一个输入,输出0(属于分类0)或1(属于分类1)。如下面所示,and运算是一个线性分类问题,即可以用一条直线把分类0(falsefalse,红叉表示)和分类1(truetrue,绿点表示)分开。
然而,感知器却不能实现异或运算,如下图所示,异或运算不是线性的,你无法用一条直线把分类0和分类1分开。
感知机训练过程统计课程中已经介绍过,这里不再赘述。
那如何解决这类问题呢?一种是像之前课堂里介绍的,SVM等解决,另一类呢,你说一个感知机不能解决,那我多加几层行不行呢?当然是可以的,神经网络从此诞生。
在正式介绍神经网络之前,不得不提它的基本单元——线性单元(神经元)。
本节通过介绍另外一种『感知器』,也就是『线性单元』,来说明关于深度学习的一些基本的概念,比如模型、目标函数、优化算法等等。这些概念对于所有的深度学习算法来说都是通用的,掌握了这些概念,就掌握了深度学习的基本套路。
感知器有一个问题,当面对的数据集不是线性可分的时候,『感知器规则』可能无法收敛,这意味着我们永远也无法完成一个感知器的训练。为了解决这个问题,我们使用一个可导的线性函数来替代感知器的阶跃函数,这种感知器就叫做线性单元。线性单元在面对线性不可分的数据集时,会收敛到一个最佳的近似上。
为了简单起见,我们可以设置线性单元的激活函数ff为 f(x)=xf(x)=x,这样的线性单元如下图所示:
对比我们前面介绍过的感知机:
这样替换了激活函数之后,线性单元将返回一个实数值而不是0,1分类。因此线性单元用来解决回归问题而不是分类问题(以概率形式也可以做分类问题) 。
线性单元的模型
当我们说模型时,我们实际上在谈论根据输入xx预测输出yy的算法。比如,xx可以是一个人的工作年限,yy可以是他的月薪,我们可以用某种算法来根据一个人的工作年限来预测他的收入。比如:
y=h(x)=w*x+by=h(x)=w∗x+b
函数h(x)h(x)叫做假设,而ww、bb是它的参数。我们假设参数w=1000w=1000,参数b=500b=500,如果一个人的工作年限是5年的话,我们的模型会预测他的月薪为
y=h(x)=1000*5+500=5500y=h(x)=1000∗5+500=5500(元)
你也许会说,这个模型太不靠谱了。你说得对~😹
因为我们考虑的因素太少了,仅仅包含了工作年限。如果考虑更多的因素,比如所处的行业、公司、职级等等,可能预测就会靠谱的多。我们把工作年限、行业、公司、职级这些信息,称之为特征。对于一个工作了5年,在IT行业,百度工作,职级T6这样的人,我们可以用这样的一个特征向量来表示他
X= (5, IT, 百度, T6)X=(5,IT,百度,T6)
既然输入XX变成了一个具备四个特征的向量,相对应的,仅仅一个参数ww就不够用了,我们应该使用4个参数w_1,w_2,w_3,w_4w1,w2,w3,w4,每个特征对应一个。这样,我们的模型就变成
y=h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+by=h(x)=w1∗x1+w2∗x2+w3∗x3+w4∗x4+b
其中,x_1x1对应工作年限,x_2x2对应行业,x_3x3对应公司,x_4x4对应职级。
为了书写和计算方便,我们可以令w_0w0等于bb,同时令w_0w0对应于特征x_0x0。由于x_0x0其实并不存在,我们可以令它的值永远为1。也即是 b=w_0*x_0,其中x_0=1b=w0∗x0,其中x0=1,这样上面的式子就可以写成
\begin{aligned} y &= h(x) \ &= w_1x_1+w_2x_2+w_3x_3+w_4x_4+b \ &= w_0x_0+w_1x_1+w_2x_2+w_3x_3+w_4*x_4 \end{aligned}y=h(x)=w1∗x1+w2∗x2+w3∗x3+w4∗x4+b=w0∗x0+w1∗x1+w2∗x2+w3∗x3+w4∗x4
我们还可以把上式写成向量的形式
y=h(x)=w^TXy=h(x)=wTX
长成这种样子模型就叫做线性模型,因为输出就是输入特征的线性组合。
线性单元的目标函数/损失函数
接下来,我们需要关心的是这个模型如何训练,也就是参数WW取什么值最合适。这是通过优化目标函数实现的。
那总得告诉我啥是目标函数吧,客官不要急,该来的一个都少不了😂
在监督学习下,对于一个样本,我们知道它的特征XX,以及标签yy。同时,我们还可以根据模型h(X)h(X)计算得到输出\overline{y}y。注意这里面我们用yy表示训练样本里面的标签,也就是实际值;用带上划线的表示模型计\overline{y}y算的出来的预测值。我们当然希望模型计算出来的\overline{y}y和yy越接近越好。
数学上有很多方法来表示\overline{y}y和yy的接近程度,比如我们可以用\overline{y}y和yy差的平方的来表示它们的接近程度
e=\frac{1}{2}(y-\overline{y})^2e=21(y−y)2
我们把ee叫做单个样本的误差。训练中会有很多样本,比如NN个,可以用所有样本的误差和来表示模型的误差EE,也即是
\begin{aligned}E & =e{(1)}+e{(2)}+\cdots+e^{(n)} \ & =\sum_{i=1}ne{(i)} \ & =\frac{1}{2}\sum_{i=1}n(y{(i)}-\overline{y}{(i)})2 \ \end{aligned}E=e(1)+e(2)+⋯+e(n)=i=1∑ne(i)=21i=1∑n(y(i)−y(i))2
其中,\begin{aligned} \overline{y}^{(i)} &= h(X^{(i)}) \ &=WTX{(i)} \end{aligned}y(i)=h(X(i))=WTX(i)
式中,e{(1)}e(1)表示第一个样本的误差,e{(2)}e(2)表示第二个样本的误差\dots\dots……。而x{(i)}x(i)表示第ii个训练样本的**特征**,y{(i)}y(i)表示第ii个样本的标签,也可以使用元组表示第ii个训练样本。\overline{y}^{(i)}y(i)则是模型对第ii个样本的预测值。
对于特定的训练数据集来说,(x{(i)},y{(i)})(x(i),y(i))都是已知的,所以上式其实是参数WW的函数:
\begin{aligned}E(W) & =\frac{1}{2}\sum_{i=1}n(y{(i)}-\overline{y}{(i)})2 \ & = \frac{1}{2}\sum_{i=1}n(y{(i)}-WTX{(i)})^2 \end{aligned}E(W)=21i=1∑n(y(i)−y(i))2=21i=1∑n(y(i)−WTX(i))2
由此可见,模型的训练,实际上就是求取到合适的WW,使E(W)E(W)取得最小值。这在数学上称作优化问题,而E(W)E(W)就是我们优化的目标,称之为目标函数。
那我们如何进行优化呢?我们在“数学基础-导数及其应用”一节已经进行过讲解,忘了的同学可以先回去补补,不补,。。。,那也没关系,后面还会讲。
正所谓欲练此功,必先自宫,若不自宫,效果相同。
上节我们介绍的线性单元,其实是神经网络的基本单元,本节我们将把这些单独的单元按照一定的规则相互连接在一起形成神经网络,从而奇迹般的获得了强大的学习能力。
神经元和感知器本质上是一样的,只不过我们说感知器的时候,它的激活函数是阶跃函数;而当我们说神经元时,激活函数往往选择为sigmoidsigmoid函数或tanhtanh函数。如下图所示:
神经元如何构成神经网络
神经网络其实就是按照一定规则连接起来的多个神经元。上图展示了一个 全连接(full connected, FC) 神经网络,通过观察上面的图,我们可以发现它的规则包括:
神经元按照层来布局。最左边的层叫做输入层,负责接收输入数据;最右边的层叫输出层,我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层,因为它们对于外部来说是不可见的。
同一层的神经元之间没有连接。
第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义),第N-1层神经元的输出就是第N层神经元的输入。
每个连接都有一个权值。
上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络,比如卷积神经网络(CNN)、循环神经网络(RNN),他们都具有不同的连接规则,这些在我们后续的教程中都会涉及。
现在提到“神经网络”和“深度神经网络”,会觉得两者没有什么区别,神经网络还能不是“深度”(deep)的吗?
能,我们常用的 Logistic regression 就可以认为是一个不含隐含层的输出层激活函数用 sigmoid(logistic) 的神经网络,显然 Logistic regression 就不是 deep 的。不过,现在神经网络基本都是 deep 的,即包含多个隐含层。Why?
通用近似定理(universality approximation theorem)
任何连续的函数f:RN→RMf:RN→RM都可以用只有一个隐含层的神经网络表示。(隐含层神经元足够多,如下图)
一个神经网络可以看成是一个从输入到输出的映射,上图中3层全链接+激活函数可以拟合任意(线性/非线性)函数,那么既然仅含一个隐含层的神经网络可以表示任何连续的函数,为什么还要多个隐含层的神经网络?甚至,单层隐藏层中,我加很多神经元,直接叫**“宽度神经网络”**得了。
为什么是深度而不是宽度?
台湾大学李宏毅教授提出过一种叫做模块化(Modularization)的解释。
在多层神经网络中,第一个隐含层学习到的特征是最简单的,之后每个隐含层使用前一层得到的特征进行学习,所学到的特征变得越来越复杂。
low levellowlevel 中每一个特征在high levelhighlevel 或多或少被使用,这样对于每一个high levelhighlevel 特征,只需要训练一套low levellowlevel 特征。是的,low levellowlevel 特征被共用了,相当于将提取low levellowlevel 特征单独成立了一个模块,供高层调用。对于每一个high levelhighlevel 特征,不需要每次都将low levellowlevel 特征训练一遍。这就是 deep 的好处。
在比较深度神经网络和仅含一个隐含层神经网络的效果时,需要控制两个网络的 trainable 参数数量相同,不然没有可比性。实验证明,相同参数数量下,deep 表现更好;这也就意味着,达到相同的效果,deep 的参数会更少。
不否认,理论上仅含一个隐含层的神经网络完全可以实现深度神经网络的效果,但是训练难度要大于深度神经网络。
仅含一个隐含层的神经网络可以拟合任意(线性/非线性)函数,可是谁用神经网络只是为了拟合训练数据?训练的意义是为了让网络可以对未知数据得出更准确的反馈。
神经网络基本单元及基础结构都介绍完了,现在可以回头来聊聊这个激活函数了。就是下图中圆圈那个东东:
为啥神经元输出的时候需要这么一个东西?我们从一个例子说起:
现在有一个二分类问题,我们要将下面的三角形和圆点进行正确的分类,我们试着用神经网络解决这个问题。跟大家说明一下,这是一个线性不可分的问题,就是你在这个平面里,找不到一条直线可以把图中的三角形和圆点完全分开。如果你能找到,请收下我的膝盖!
尝试用不带激活函数的单层感知机来解决
左图是一个单层的感知机结构,其中w_1、w_2w1、w2是网络上权重,bb是偏置量。左图是一个没有激活函数单层感知机,它的工作原理是:输入特征x_1x1和特征x_2x2,如果y>0y>0,证明是正类;如果y<0y<0,证明是负类。我们这里不讨论y=0y=0的特殊情况。根据单层感知机的工作原理,我们画出右边的坐标图。**不带激活函数的单层感知机是一个线性分类器,不能解决线性不可分的问题。**之前我们就说过,单层感知机不能解决非线性问题,那我们多层试试。
用不带激活函数的多个感知机来解决
大家看一下,合并后的式子,还是一个关于x_1x1和x_2x2的线性表达式,合并后的多个感知器本质上还是一个线性分类器,还是解决不了非线性的问题。
事实上,不带激活函数的网络,多层与单层的表达能力没多少差别——都是线性组合。
不管是单层感知机还是多个感知器,只要不带激活函数,都只能解决线性可分的问题。解决不了我们的线性不可分问题。不信,那我们就在平面中画几条直线试试,结果发现这几条直线无论在平面中如何旋转,都不能完全正确的分开三角形和圆点。
在上面的线性方程的组合过程中,其实类似的在做三条直线的线性组合,最多也就是更复杂的线性组合罢了。有人在这里又要抖机灵了!我数学学的好,我记得学高等数学的时候,在不定积分那一块,有个画曲为直思想来近似求解。那么,我们可以来借鉴一下,用无数条直线去近似接近一条曲线,你很聪明啊!但是比着用非线性的激活函数来说,你这解决办法还是太低端了一些。
抛开神经网络中神经元需不需要激活函数这点不说,如果没有激活函数,仅仅是线性函数的组合解决的问题太有限了,碰到非线性问题就束手无策了。那么加入激活函数是否能够解决呢?
激活函数作用
我们再设计一个神经网络,在所有的隐层和输出层加一个激活函数,这里激活函数就用SigmoidSigmoid函数,这样yy输出的就是一个非线性函数了,yy的输出更复杂,有了这样的非线性激活函数以后,神经网络的表达能力更加强大了。能不能解决我们一开始提出的线性不可分问题呢?
把上图中的带有激活函数的单层感知机扩展到带有激活函数的多个神经元的情况。那么神经网络的表达能力更强:
相应的非线性组合示意图:
最后,通过最优化损失函数的做法,通过不断的学习,能够学到正确分类三角形和圆点的曲线。具体学到什么曲线,我们不知道,或许是下图所示的曲线,也可能是其他曲线。
总结
激活函数是用来加入非线性因素的,提高神经网络对模型的表达能力,解决线性模型所不能解决的问题。
神经网络训练过程,反向传播算法请参看之前介绍的数学基础-导数及其应用。
扩展阅读
2.李宏毅教授PPT(300页)(初学非常好的一个PPT,已上传到我的网盘:链接:https://pan.baidu.com/s/1srhBo_CnT6I5qwezSvVGqg 提取码:9r3c)
本部分我们从深度学习的基本概念入手,到神经网络学习的核心部件——反向传播算法,讲得比较浅,但是往后的套路都是一样的,接下来我们将深入到深度学习的一些经典网络卷积神经网络CNN系列。
以识别MNISTMNIST数据集为例
在前面的小节中,我们介绍了全连接神经网络,以及它的训练和使用(1.2.6节的扩展阅读例子)。本节我们简化一下这个例子,仅仅用它来识别了手写数字“88”。
机器/深度学习只有在你拥有数据的情况下,最好是大量的数据,才能有效。所以,我们需要有大量的手写“8”来开始我们的尝试。幸运的是,恰好有研究人员创造出了“MNISTMNIST手写数字数据库”能助我们一臂之力。MNISTMNIST提供了60,000张手写数字的图片,每一张都是一个18×18的图片。下列是数据库中的一些例子:MNISTMNIST数据库中的数字“8”
如何把一张图输入神经网络呢?前面我们提到过,图像可以用一个矩阵来表征,每一个值代表其灰度值/像素值:
我们将这张18×1818×18像素的图片当成一串324个数字的数列,就可以把它输入到我们的神经网络里面了:
为了更好地操控我们的输入数据,我们将神经网络也扩大到拥有324个输入节点:
对应有两个输出:第一个输出会预测图片是“8”的概率 而第二个则输出不是“8”的概率。概括地说,我们就可以依靠多种不同的输出,利用神经网络把要识别的物品进行分组。
现在唯一要做的就是训练神经网络了。用各种“8”和非“8”的图片来训练,这样它就能学习怎么去区分了。当我们输入一个“8”的时候,我们会告诉他“是8的概率”是100%而“不是8的概率”是0%,反之亦然。以下为一些训练数据:
在我们笔记本电脑上面用几分钟的时间就能训练完成这种神经网络。完成之后就可以得到一个有着很高的“8”图片识别率的神经网络。
脑纸:哇哈哈哈,这么简单,我会了!
手:呵呵呵,你会个屁~
当然不会这么简单,大家想想以下几种场景:
首先,当我们的数字就在图片的正中间的时候,我们的分类器干得还不错:
然而,当数字并不是正好在图片中央的时候,我们的分类器就GGGG了。一点点的位移分类器就掀桌子不干了(╯‵□′)╯︵┻━┻:
这是因为我们的网络只学习到了正中央的“8”。它并不知道那些偏离中心的“8”长什么样子。它仅仅知道中间是“8”的规律。泛化性能太差。
在真实世界中,这好像并没什么卵用。真实世界的问题永远不会如此轻松简单。所以,我们需要知道,怎么才能让我们的神经网络在非中心“8”的情况下识别。
不改变网络(全连接)的情况下解决方案:
滑窗搜索
现在已经有了一个能够很好地识别图片中间“8”的模型,试想,如果我们干脆把整个图片分成一个个小部分,并挨个都识别一遍,直到我们找到“8”,这样能不能行呢?
这个叫做**滑窗(Sliding Window)**法,是暴力算法之一。在有限的情况下,它能够识别的很好。但实际上它并不怎么有效率,你必须在同一张图片里面一遍一遍的识别不同大小的物体。实际上,我们可以做得更好。
加大数据集与更深的网络
如果我们用更多的数据来训练,数据中包括各种不同位置和大小的“8”,会怎样呢?
实际上,并不需要收集更多的训练数据,我们可以写一个小脚本来生成各种各样不同位置“8”的新图片:
使用这种方法,我们能够轻易地创造出无限量的训练数据。
更多的数据让我们的神经网络更难解决这个问题。但是把神经网络扩大,它就能寻找到更复杂的规律了,以此来弥补解决困难问题的不足。
要扩大我们的网络,我们首先要把把节点一层一层的堆积起来:
也就是我们前文提到的深度神经网络DNN。
这个想法在1960年代末就出现了,但直至今日,训练这样一个大型神经网络也是一件不切实际的缓慢的事情。另外,如果把图片最上方和最下方的“8”当成两个不同的对象来处理,并写两个不同的网络来识别它们,这件事实在是说不通。
上述可知,全连接这种结构的网络对于图像识别任务来说并不是很合适。本节将要介绍一种更适合图像、语音识别等任务的神经网络结构——卷积神经网络(Convolutional Neural Network, CNNConvolutionalNeuralNetwork,CNN)。说卷积神经网络是最重要的一种神经网络也不为过,它在最近几年大放异彩,几乎所有图像、语音识别领域的重要突破都是卷积神经网络取得的。
我们从一个简单的例子入手,作为人类,你能够直观的感知到图片中存在某种层级(Hierarchy)或者是概念结构(Conceptual structure)。如下图:
看见这张图,你立刻就能识别出这个图片的层级:
地面是由草和水泥组成的
有一个小孩在图片中
小孩在骑弹簧木马
弹簧木马在草地上
最重要的一点是识别出了“小孩”,无论这个小孩所处的环境是怎样的。当每一次出现不同的环境时,我们不需要重新学习“小孩”这个概念。
但是现在,上文神经网络做不到这些。它认为“8”出现在图片的不同位置,就是不一样的东西。它不能理解“物体出现在图片的不同位置还是同一个物体”这个概念。这意味着在每种可能出现的位置上,它必须重新学习识别各种物体。这是不是弱爆了。
我们需要让我们的神经网络理解“平移不变性(Translation invariance)”这个概念——也就是说,“8”无论出现在图片的哪里,它都是“8”。
我们会通过一个叫做卷积(Convolution)的方法来达成这个目标。卷积的灵感是由计算机科学和生物学共同激发的。
卷积是如何工作的?
之前提到过,可以把一整张图片当做一串数字输入到神经网络里面。不同的是,这次我们会利用“平移不变性”的概念来把这件事做得更智能。
分步解释——
第一步:把图片分解成部分重合的小图块
和上述的滑窗搜索类似的,我们把滑框在整个图片上滑过,并存储下每一个框里面的小图块(把图片分解成了77块同样大小的小图块):
之前,我们把一张图片输入到神经网络中来看这张图片是不是一个“8”。这一次我们还做同样的事情,只不过我们输入的是一个个小图块:
然而,有一个非常重要的不同:对于每个小图块,我们会使用同样的神经网络权重。换一句话来说,我们同样对待每一个小图块。如果哪个小图块输出有任何异常(值变高),我们就认为这个图块是感兴趣的。
大家可以回顾一下“数学基础——线性代数”的卷积示图:
第三步:把每一个小图块的结果都保存到一个新的矩阵当中
我们不想并不想打乱小图块的顺序。所以把每个小图片按照图片上的顺序输入并保存结果,就像这样:
换一句话来说,我们从一整张图片开始,最后得到一个稍小一点的矩阵,里面存储着我们图片中的哪一部分是感兴趣的。
第四步:缩减像素采样
第三步的结论是一个数列,这个数列对应着原始图片中哪一部分最感兴趣。但是这个数列依然很大:
为了减小这个数列的大小,我们利用一种叫做 最大池化(Max Pooling) 的方法来降采样:
以2×2的方阵矩阵为例,取最大值:
即,针对每一个小图框,我们保留了最感兴趣的部分。
最后一步:作出预测
到现在为止,我们已经把一个很大的图片,缩减到了一个相对较小的矩阵。
你猜怎么着?矩阵就是一序列数而已,所以我们我们可以把这个矩阵输入到另外一个神经网络里面去。最后的这个神经网络会决定这个图片是否匹配。为了区分它和卷积的不同,我们把它称作“完全连接”网络(”Fully Connected” Network)
所以从开始到结束,我们的五步就像管道一样连接起来:
我们的图片处理是一系列的步骤:卷积,最大池化,还有最后的“完全连接”网络。你可以把这些步骤组合、堆叠任意多次,来解决真实世界的问题。你可以有2层,3层或者10层卷积层。当你想要缩小你的数据大小的时候,你也随时可以调用最大池化函数。我们解决问题的基本方法,就是从一整个图片开始,一步一步逐渐的分解它,直到你找到了一个单一的结论。你的卷积层越多,你的网络就越能识别出复杂的特征。
本部分将总结上述CNN图像识别例子,系统性介绍CNN。
通过上述CNN图像识别例子,我们可以得出CNN的通用性结构:
如上图,一个卷积神经网络由若干卷积层、Pooling层、全连接层组成。你可以构建各种不同的卷积神经网络,它的常用架构模式为:
INPUT -> [[CONV]*N -> POOL?]*M -> [FC]*K
也就是N个卷积层叠加,然后(可选)叠加一个Pooling层,重复这个结构M次,最后叠加K个全连接层。
对于上图展示的卷积神经网络:
INPUT -> CONV -> POOL -> CONV -> POOL -> FC -> FC
按照上述模式可以表示为:
INPUT -> [[CONV]*1 -> POOL]*2 -> [FC]*2
也就是:N=1, M=2, K=2。
三维的层结构
从上图中可以发现,卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的,也就是排成一条线的样子;而卷积神经网络每层的神经元是按照三维排列的,也就是排成一个长方体的样子,有宽度、高度和深度。
对于上图展示的神经网络,输入层的宽度和高度对应于输入图像的宽度和高度,而它的深度为1(如,灰度值)。接着,第一个卷积层对这幅图像进行了卷积操作(后面我们会讲如何计算卷积),得到了三个Feature Map。这里的"3"可能是让很多初学者迷惑的地方,实际上,就是这个卷积层包含三个Filter,也就是三套参数,每个Filter都可以把原始输入图像卷积得到一个Feature Map,三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter,那是可以自由设定的。也就是说,卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征,也就是得到了三个Feature Map,也称做三个通道(channel)。
这里的Filter可以简单的理解为:不同的Filter检测不同的特征,如检测小鼠图片的曲线、圆圈等。
在第一个卷积层之后,Pooling层对三个Feature Map做了下采样(后面我们会讲如何计算下采样),得到了三个更小的Feature Map。接着,是第二个卷积层,它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起,得到一个新的Feature Map。这样,5个Filter就得到了5个Feature Map。接着,是第二个Pooling,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
最后两层是全连接层。第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
至此,我们对卷积神经网络有了最基本的感性认识。接下来,我们将介绍卷积神经网络中各种层的计算和训练。
卷积层输出的计算
先用一个简单的例子来讲解如何计算卷积,然后再抽象卷积层的一些重要概念和计算方法。
假设有一个5 x 5的图像,使用一个3 x 3的filter进行卷积,想得到一个3 x 3的Feature Map,如下所示:
为了清楚的描述卷积计算过程,我们首先对图像的每个像素进行编号,用x_{i,j}xi,j表示图像的第ii行第jj列元素;对filter的每个权重进行编号,用w_{m,n}wm,n表示第mm行第nn列权重,用w_bwb表示filter的偏置项;对Feature Map的每个元素进行编号,用a_{i,j}ai,j表示Feature Map的第ii行第jj列元素;用ff表示激活函数(以relu函数作为激活函数为例)。然后,使用下列公式计算卷积:
a_{i,j}=f(\sum_{m=0}2\sum_{n=0}2w_{m,n}x_{i+m,j+n}+w_b)ai,j=f(∑m=02∑n=02wm,nxi+m,j+n+wb)
例如,对于Feature Map左上角元素a_{0,0}a0,0来说,其卷积计算方法为:
\begin{aligned} a_{i,j} &=f(\sum_{m=0}2\sum_{n=0}2w_{m,n}x_{i+m,j+n}+w_b) \ &=relu(w_{0,0}x_{0,0}+w_{0,1}x_{0,1}+w_{0,2}x_{0,2}+w_{1,0}x_{1,0}+w_{1,1}x_{1,1}+\cdots) \ &=relu(1+0+1+0+1+0+0+0+1+0) \ &=relu(4) \ &=4 \end{aligned}ai,j=f(m=0∑2n=0∑2wm,nxi+m,j+n+wb)=relu(w0,0x0,0+w0,1x0,1+w0,2x0,2+w1,0x1,0+w1,1x1,1+⋯)=relu(1+0+1+0+1+0+0+0+1+0)=relu(4)=4
Relu函数定义为:
f(x)=max(0,x)f(x)=max(0,x)
计算结果如下图:
可以依次计算出Feature Map中所有元素的值。下面的动画显示了整个Feature Map的计算过程:
上面的计算过程中,步幅(stride)为1。步幅可以设为大于1的数。例如,当步幅为2时,Feature Map计算如下:
注意到,当步幅设置为2的时候,Feature Map就变成2 x 2了。这说明图像大小、步幅和卷积后的Feature Map大小是有关系的。事实上,它们满足下面的关系:
W_2=(W_1-F+2P)/S+1W2=(W1−F+2P)/S+1
H_2=(H_1-F+2P)/S+1H2=(H1−F+2P)/S+1
在上面两个公式中,W_2W2卷积后Feature Map的宽度;W_1W1是卷积前图像的宽度;FF是filter的宽度;PP是Zero Padding数量,Zero Padding是指在原始图像周围补几圈0,如果PP的值是1,那么就补1圈0;SS是步幅;H_2H2是卷积后Feature Map的高度;H_1H1是卷积前图像的高度。
前面我们已经讲了深度为1的卷积层的计算方法,如果深度大于1怎么计算呢?其实也是类似的。如果卷积前的图像深度为D,那么相应的filter的深度也必须为D。我们扩展一下,得到了深度大于1的卷积计算公式:
a_{i,j}=f(\sum_{d=0}{D-1}\sum_{m=0}{F-1}\sum_{n=0}^{F-1}w_{d,m,n}x_{d,i+m,j+n}+w_b)ai,j=f(∑d=0D−1∑m=0F−1∑n=0F−1wd,m,nxd,i+m,j+n+wb)
式中,D是深度;F是filter的大小(宽度或高度,两者相同);w_{d,m,n}wd,m,n表示filter的第dd层第mm行第nn列权重;a_{d,i,j}ad,i,j表示图像的第dd层第ii行第jj列像素。
我们前面还曾提到,每个卷积层可以有多个filter。每个filter和原始图像进行卷积后,都可以得到一个Feature Map。因此,卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的。
下面的动画显示了包含两个filter的卷积层的计算。我们可以看到7 x 7 x 3输入,经过两个3 x 3 x 3的filter卷积(步幅为2),得到了3 x 3 x 2的输出。另外我们也会看到下图的Zero padding是1,也就是在输入元素的周围补了一圈0。Zero padding对于图像边缘部分的特征提取是很有帮助的。
以上就是卷积层的计算方法。这里面体现了局部连接和权值共享:每层神经元只和上一层部分神经元相连(卷积计算规则),且filter的权值对于上一层所有神经元都是一样的。对于包含两个3 x 3 x 3的fitler的卷积层来说,其参数数量仅有(3 x 3 x 3+1) x 2=56个,且参数数量与上一层神经元个数无关。与全连接神经网络相比,其参数数量大大减少了。
以上过程及高维的卷积计算的数学公式,大家可以自己找找资料,不影响理解,此处就不提出了。
Pooling层输出值的计算
Pooling层主要的作用是下采样,通过去掉Feature Map中不重要的特征,进一步减少参数数量。Pooling的方法很多,最常用的是Max Pooling。Max Pooling实际上就是在n x n的图像中取最大值,作为采样后的值。下图是2 x 2 max pooling:
除了Max Pooing之外,常用的还有Mean Pooling——取平均值。
对于深度为D的Feature Map,各层独立做Pooling,因此Pooling后的深度仍然为D。
全连接层输出值的计算与前述计算方法一样,此处不再赘述。
另外,卷积神经网络的的训练原理与神经网络训练过程相同,可参看数学基础-导数及其应用,此处不再赘述。
全连接网络 VS 卷积网络
全连接神经网络之所以不太适合图像识别任务,主要有以下几个方面的问题:
参数数量太多 考虑一个输入1000 x 1000像素的图片(一百万像素,现在已经不能算大图了),输入层有1000 x 1000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多),那么仅这一层就有(1000 x 1000+1) x 100=1亿参数,这实在是太多了!我们看到图像只扩大一点,参数数量就会多很多,因此它的扩展性很差。
没有利用像素之间的位置信息 对于图像识别任务来说,每个像素和其周围像素的联系是比较紧密的,和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连,那么就相当于对于一个像素来说,把图像的所有像素都等同看待,这不符合前面的假设。当我们完成每个连接权重的学习之后,最终可能会发现,有大量的权重,它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重,这样的学习必将是非常低效的。
网络层数限制 网络层数越多其表达能力越强,但是通过梯度下降方法训练深度全连接神经网络很困难,因为全连接神经网络的梯度很难传递超过3层。因此,我们不可能得到一个很深的全连接神经网络,也就限制了它的能力。
那么,卷积神经网络又是怎样解决这个问题的呢?主要有三个思路:
局部连接 这个是最容易想到的,每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连。这样就减少了很多参数。
权值共享 一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。
下采样 可以使用Pooling来减少每层的样本数,进一步减少参数数量,同时还可以提升模型的鲁棒性。
对于图像识别任务来说,卷积神经网络通过尽可能保留重要的参数,去掉大量不重要的参数,来达到更好的学习效果。
卷积神经网络可谓是现在深度学习领域中大红大紫的网络框架,尤其在计算机视觉领域更是一枝独秀。CNN从90年代的LeNet开始,21世纪初沉寂了10年,直到12年AlexNet开始又再焕发第二春,从ZF Net到VGG,GoogLeNet再到ResNet和最近的DenseNet,网络越来越深,架构越来越复杂,解决反向传播时梯度消失的方法也越来越巧妙。今天,我们简要过一波CNN的各种经典架构,领略一下CNN的发展历程中各路大神之间的智慧碰撞之美。
本节将会谈到以下经典的卷积神经网络:LeNet,AlexNet,ZF,VGG,GoogLeNet,ResNet,DenseNet。
开山之作:LeNet
闪光点:定义了CNN的基本组件,是CNN的鼻祖。
LeNet是卷积神经网络的祖师爷LeCun在1998年提出,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。如今各大深度学习框架中所使用的LeNet都是简化改进过的LeNet-5(-5表示具有5个层),和原始的LeNet有些许不同,比如把激活函数改为了现在很常用的ReLu。
LeNet-5跟现有的conv->pool->ReLU的套路不同,它使用的方式是conv1->pool->conv2->pool2再接全连接层,但是不变的是,卷积层后紧接池化层的模式依旧不变。
以上图为例,对经典的LeNet-5做深入分析:
首先输入图像是单通道的28*28大小的图像,用矩阵表示就是[1,28,28]
第一个卷积层conv1所用的卷积核尺寸为5*5,滑动步长为1,卷积核数目为20,那么经过该层后图像尺寸变为24,28-5+1=24,输出矩阵为[20,24,24]。
第一个池化层pool核尺寸为2*2,步长2,这是没有重叠的max pooling,池化操作后,图像尺寸减半,变为12×12,输出矩阵为[20,12,12]。
第二个卷积层conv2的卷积核尺寸为5*5,步长1,卷积核数目为50,卷积后图像尺寸变为8,这是因为12-5+1=8,输出矩阵为[50,8,8].
第二个池化层pool2核尺寸为2*2,步长2,这是没有重叠的max pooling,池化操作后,图像尺寸减半,变为4×4,输出矩阵为[50,4,4]。
pool2后面接全连接层fc1,神经元数目为500,再接relu激活函数。
再接fc2,神经元个数为10,得到10维的特征向量,用于10个数字的分类训练,送入softmaxt分类,得到分类结果的概率output。
王者归来:AlexNet
AlexNet在2012年ImageNet竞赛中以超过第二名10.9个百分点的绝对优势一举夺冠,从此深度学习和卷积神经网络名声鹊起,深度学习的研究如雨后春笋般出现,AlexNet的出现可谓是卷积神经网络的王者归来。
闪光点:
更深的网络
数据增广
ReLU
dropout
LRN
以上图AlexNet架构为例,这个网络前面5层是卷积层,后面三层是全连接层,最终softmax输出是1000类,取其前两层进行详细说明。
AlexNet共包含5层卷积层和三层全连接层,层数比LeNet多了不少,但卷积神经网络总的流程并没有变化,只是在深度上加了不少。
AlexNet针对的是1000类的分类问题,输入图片规定是256×256的三通道彩色图片,为了增强模型的泛化能力,避免过拟合,作者使用了随机裁剪的思路对原来256×256的图像进行随机裁剪,得到尺寸为3×224×224的图像,输入到网络训练。
因为使用多GPU训练,所以可以看到第一层卷积层后有两个完全一样的分支,以加速训练。
针对一个分支分析:第一层卷积层conv1的卷积核尺寸为11×11,滑动步长为4,卷积核数目为48。卷积后得到的输出矩阵为[48,55,55]。这里的55是个难以理解的数字,作者也没有对此说明,如果按照正常计算的话(224-11)/4+1 != 55的,所以这里是做了padding再做卷积的,即先padiing图像至227×227,再做卷积(227-11)/4+1 = 55。这些像素层经过relu1单元的处理,生成激活像素层,尺寸仍为2组48×55×55的像素层数据。然后经过归一化处理,归一化运算的尺度为5*5。第一层卷积运算结束后形成的像素层的规模为48×27×27。
输入矩阵是[48,55,55].接着是池化层,做max pooling操作,池化运算的尺度为3*3,运算的步长为2,则池化后图像的尺寸为(55-3)/2+1=27。所以得到的输出矩阵是[48,27,27]。后面层不再重复叙述。
AlexNet用到训练技巧:
数据增广技巧来增加模型泛化能力。
用ReLU代替Sigmoid来加快SGD的收敛速度
Dropout: Dropout原理类似于浅层学习算法的中集成算法,该方法通过让全连接层的神经元(该模型在前两个全连接层引入Dropout)以一定的概率失去活性(比如0.5)失活的神经元不再参与前向和反向传播,相当于约有一半的神经元不再起作用。在测试的时候,让所有神经元的输出乘0.5。Dropout的引用,有效缓解了模型的过拟合。
Local Responce Normalization:局部响应归一层的基本思路是,假如这是网络的一块,比如是 13×13×256, LRN 要做的就是选取一个位置,比如说这样一个位置,从这个位置穿过整个通道,能得到 256 个数字,并进行归一化。进行局部响应归一化的动机是,对于这张 13×13 的图像中的每个位置来说,我们可能并不需要太多的高激活神经元。但是后来,很多研究者发现 LRN 起不到太大作用,因为并不重要,而且我们现在并不用 LRN 来训练网络。
稳步前行:ZF-Net
ZFNet是2013ImageNet分类任务的冠军,其网络结构没什么改进,只是调了调参,性能较Alex提升了不少。ZF-Net只是将AlexNet第一层卷积核由11变成7,步长由4变为2,第3,4,5卷积层转变为384,384,256。这一年的ImageNet还是比较平静的一届,其冠军ZF-Net的名堂也没其他届的经典网络架构响亮。
越走越深:VGG-Nets
VGG-Nets是由牛津大学VGG(Visual Geometry Group)提出,是2014年ImageNet竞赛定位任务的第一名和分类任务的第二名的中的基础网络。VGG可以看成是加深版本的AlexNet. 都是conv layer + FC layer,在当时看来这是一个非常深的网络了,因为层数高达十多层,我们从其论文名字就知道了(《Very Deep Convolutional Networks for Large-Scale Visual Recognition》),当然以现在的目光看来VGG真的称不上是一个very deep的网络。
上面一个表格是描述的是VGG-Net的网络结构以及诞生过程。为了解决初始化(权重初始化)等问题,VGG采用的是一种Pre-training的方式,这种方式在经典的神经网络中经常见得到,就是先训练一部分小网络,然后再确保这部分网络稳定之后,再在这基础上逐渐加深。表中从左到右体现的就是这个过程,并且当网络处于D阶段的时候,效果是最优的,因此D阶段的网络也就是VGG-16了!E阶段得到的网络就是VGG-19了!VGG-16的16指的是conv+fc的总层数是16,是不包括max pool的层数!
下面这个图就是VGG-16的网络结构。
由上图看出,VGG-16的结构非常整洁,深度较AlexNet深得多,里面包含多个conv->conv->max_pool这类的结构,VGG的卷积层都是same的卷积,即卷积过后的输出图像的尺寸与输入是一致的,它的下采样完全是由max pooling来实现。
VGG网络后接3个全连接层,filter的个数(卷积后的输出通道数)从64开始,然后每接一个pooling后其成倍的增加,128、512,VGG的主要贡献是使用小尺寸的filter,及有规则的卷积-池化操作。
闪光点:
卷积层使用更小的filter尺寸和间隔
与AlexNet相比,可以看出VGG-Nets的卷积核尺寸还是很小的,比如AlexNet第一层的卷积层用到的卷积核尺寸就是11*11,这是一个很大卷积核了。而反观VGG-Nets,用到的卷积核的尺寸无非都是1×1和3×3的小卷积核,可以替代大的filter尺寸。
3×3卷积核的优点:
多个3×3的卷基层比一个大尺寸filter卷基层有更多的非线性,使得判决函数更加具有判决性
多个3×3的卷积层比一个大尺寸的filter有更少的参数,假设卷基层的输入和输出的特征图大小相同为C,那么三个3×3的卷积层参数个数3×(3×3×C×C)=27CC;一个7×7的卷积层参数为49CC;所以可以把三个3×3的filter看成是一个7×7filter的分解(中间层有非线性的分解)
1*1卷积核的优点:
作用是在不影响输入输出维数的情况下,对输入进行线性形变,然后通过Relu进行非线性处理,增加网络的非线性表达能力。
大浪推手:GoogLeNet
GoogLeNet在2014的ImageNet分类任务上击败了VGG-Nets夺得冠军,其实力肯定是非常深厚的,GoogLeNet跟AlexNet,VGG-Nets这种单纯依靠加深网络结构进而改进网络性能的思路不一样,它另辟幽径,在加深网络的同时(22层),也在网络结构上做了创新,引入Inception结构代替了单纯的卷积+激活的传统操作(这思路最早由Network in Network提出)。GoogLeNet进一步把对卷积神经网络的研究推上新的高度。
闪光点:
引入Inception结构
中间层的辅助LOSS单元
后面的全连接层全部替换为简单的全局平均pooling
上图结构就是Inception,结构里的卷积stride都是1,另外为了保持特征响应图大小一致,都用了零填充。最后每个卷积层后面都立刻接了个ReLU层。在输出前有个叫concatenate的层,直译的意思是“并置”,即把4组不同类型但大小相同的特征响应图一张张并排叠起来,形成新的特征响应图。Inception结构里主要做了两件事:1. 通过3×3的池化、以及1×1、3×3和5×5这三种不同尺度的卷积核,一共4种方式对输入的特征响应图做了特征提取。2. 为了降低计算量。同时让信息通过更少的连接传递以达到更加稀疏的特性,采用1×1卷积核来实现降维。
这里想再详细谈谈1×1卷积核的作用,它究竟是怎么实现降维的。现在运算如下:下面动图中上图是3×3卷积核的卷积,下图是1×1卷积核的卷积过程。对于单通道输入,1×1的卷积确实不能起到降维作用,但对于多通道输入,就不不同了。假设你有256个特征输入,256个特征输出,同时假设Inception层只执行3×3的卷积。这意味着总共要进行 256×256×3×3的卷积(589000次乘积累加(MAC)运算)。这可能超出了我们的计算预算,比方说,在Google服务器上花0.5毫秒运行该层。作为替代,我们决定减少需要卷积的特征的数量,比如减少到64(256/4)个。在这种情况下,我们首先进行256到64的1×1卷积,然后在所有Inception的分支上进行64次卷积,接着再使用一个64到256的1×1卷积。
256×64×1×1 = 16000
64×64×3×3 = 36000
64×256×1×1 = 16000
现在的计算量大约是70000(即16000+36000+16000),相比之前的约600000,几乎减少了10倍。这就通过小卷积核实现了降维。
现在再考虑一个问题:为什么一定要用1×1卷积核,3×3不也可以吗?考虑[50,200,200]的矩阵输入,我们可以使用20个1×1的卷积核进行卷积,得到输出[20,200,200]。有人问,我用20个3×3的卷积核不是也能得到[20,200,200]的矩阵输出吗,为什么就使用1×1的卷积核?我们计算一下卷积参数就知道了,对于1×1的参数总数:20×200×200×(1×1),对于3×3的参数总数:20×200×200×(3×3),可以看出,使用1×1的参数总数仅为3×3的总数的九分之一!所以我们使用的是1×1卷积核。
GoogLeNet网络结构中有3个LOSS单元,这样的网络设计是为了帮助网络的收敛。在中间层加入辅助计算的LOSS单元,目的是计算损失时让低层的特征也有很好的区分能力,从而让网络更好地被训练。在论文中,这两个辅助LOSS单元的计算被乘以0.3,然后和最后的LOSS相加作为最终的损失函数来训练网络。
GoogLeNet还有一个闪光点值得一提,那就是将后面的全连接层全部替换为简单的全局平均pooling,在最后参数会变的更少。而在AlexNet中最后3层的全连接层参数差不多占总参数的90%,使用大网络在宽度和深度允许GoogleNet移除全连接层,但并不会影响到结果的精度,在ImageNet中实现93.3%的精度,而且要比VGG还要快。
里程碑式创新:ResNet
2015年何恺明推出的ResNet在ISLVRC和COCO上横扫所有选手,获得冠军。ResNet在网络结构上做了大创新,而不再是简单的堆积层数,ResNet在卷积神经网络的新思路,绝对是深度学习发展历程上里程碑式的事件。
闪光点:
层数非常深,已经超过百层
引入残差单元来解决退化问题
从前面可以看到,随着网络深度增加,网络的准确度应该同步增加,当然要注意过拟合问题。但是网络深度增加的一个问题在于这些增加的层是参数更新的信号,因为梯度是从后向前传播的,增加网络深度后,比较靠前的层梯度会很小。这意味着这些层基本上学习停滞了,这就是梯度消失问题。深度网络的第二个问题在于训练,当网络更深时意味着参数空间更大,优化问题变得更难,因此简单地去增加网络深度反而出现更高的训练误差,深层网络虽然收敛了,但网络却开始退化了,即增加网络层数却导致更大的误差,比如下图,一个56层的网络的性能却不如20层的性能好,这不是因为过拟合(训练集训练误差依然很高),这就是烦人的退化问题。残差网络ResNet设计一种残差模块让我们可以训练更深的网络。
这里详细分析一下残差单元来理解ResNet的精髓。
从下图可以看出,数据经过了两条路线,一条是常规路线,另一条则是捷径(shortcut),直接实现单位映射的直接连接的路线,这有点类似与电路中的“短路”。通过实验,这种带有shortcut的结构确实可以很好地应对退化问题。我们把网络中的一个模块的输入和输出关系看作是y=H(x)y=H(x),那么直接通过梯度方法求H(x)H(x)就会遇到上面提到的退化问题,如果使用了这种带shortcut的结构,那么可变参数部分的优化目标就不再是H(x)H(x),若用F(x)F(x)来代表需要优化的部分的话,则H(x)=F(x)+xH(x)=F(x)+x,也就是F(x)=H(x)-xF(x)=H(x)−x。因为在单位映射的假设中y=xy=x就相当于观测值,所以F(x)F(x)就对应着残差,因而叫残差网络。为啥要这样做,因为作者认为学习残差F(X)F(X)比直接学习H(X)H(X)简单!设想下,现在根据我们只需要去学习输入和输出的差值就可以了,绝对量变为相对量(H(x)- xH(x)−x 就是输出相对于输入变化了多少),优化起来简单很多。
考虑到xx的维度与F(X)F(X)维度可能不匹配情况,需进行维度匹配。这里论文中采用两种方法解决这一问题(其实是三种,但通过实验发现第三种方法会使performance急剧下降,故不采用):
zero_padding:对恒等层进行0填充的方式将维度补充完整。这种方法不会增加额外的参数
projection:在恒等层采用1x1的卷积核来增加维度。这种方法会增加额外的参数
下图展示了两种形态的残差模块,左图是常规残差模块,有两个3×3卷积核卷积核组成,但是随着网络进一步加深,这种残差结构在实践中并不是十分有效。针对这问题,右图的“瓶颈残差模块”(bottleneck residual block)可以有更好的效果,它依次由1×1、3×3、1×1这三个卷积层堆积而成,这里的1×1的卷积能够起降维或升维的作用,从而令3×3的卷积可以在相对较低维度的输入上进行,以达到提高计算效率的目的。
继往开来:DenseNet
自Resnet提出以后,ResNet的变种网络层出不穷,都各有其特点,网络性能也有一定的提升。本节介绍的最后一个网络是CVPR 2017最佳论文DenseNet,论文中提出的DenseNet(Dense Convolutional Network)主要还是和ResNet及Inception网络做对比,思想上有借鉴,但却是全新的结构,网络结构并不复杂,却非常有效,在CIFAR指标上全面超越ResNet。可以说DenseNet吸收了ResNet最精华的部分,并在此上做了更加创新的工作,使得网络性能进一步提升。
闪光点:
密集连接:缓解梯度消失问题,加强特征传播,鼓励特征复用,极大的减少了参数量
DenseNet 是一种具有密集连接的卷积神经网络。在该网络中,任何两层之间都有直接的连接,也就是说,网络每一层的输入都是前面所有层输出的并集,而该层所学习的特征图也会被直接传给其后面所有层作为输入。下图是 DenseNet 的一个dense block示意图,一个block里面的结构如下,与ResNet中的BottleNeck基本一致:BN-ReLU-Conv(1×1)-BN-ReLU-Conv(3×3) ,而一个DenseNet则由多个这种block组成。每个DenseBlock的之间层称为transition layers,由BN−>Conv(1×1)−>averagePooling(2×2)组成
密集连接不会带来冗余吗?不会!密集连接这个词给人的第一感觉就是极大的增加了网络的参数量和计算量。但实际上 DenseNet 比其他网络效率更高,其关键就在于网络每层计算量的减少以及特征的重复利用。DenseNet则是让l层的输入直接影响到之后的所有层,它的输出为:x_l=H_l([X_0,X_1,…,x_{l−1}])xl=Hl([X0,X1,…,xl−1]),其中[x_0,x_1,…,x_{l−1}][x0,x1,…,xl−1]就是将之前的feature map以通道的维度进行合并。并且由于每一层都包含之前所有层的输出信息,因此其只需要很少的特征图就够了,这也是为什么DneseNet的参数量较其他模型大大减少的原因。这种dense connection相当于每一层都直接连接input和loss,因此就可以减轻梯度消失现象,这样更深网络不是问题
需要明确一点,dense connectivity 仅仅是在一个dense block里的,不同dense block 之间是没有dense connectivity的,比如下图所示。
天底下没有免费的午餐,网络自然也不例外。在同层深度下获得更好的收敛率,自然是有额外代价的。其代价之一,就是其恐怖如斯的内存占用。
本博客所有内容仅供学习,不为商用,如有侵权,请联系博主谢谢。
[1] 李宏毅,Deep Learning Tutorial,2018
[2] 深度学习发展历史 https://zhuanlan.zhihu.com/p/29096536
[5] DNNDNN图像识别:https://www.zhihu.com/question/27790364/answer/139169059
[7] CNN经典网络:https://www.cnblogs.com/skyfsm/p/8451834.html

 随时随地看视频
随时随地看视频




