【吴恩达 机器学习】线性回归算法Matlab实现

一，单变量线性回归：

1. 数据分布，x轴是属性城市人口，y轴是标签值盈利：

2. 目的：使用一个线性函数去拟合上面这些数据；

该线性函数如下只有两个参数，利用梯度下降找出使损失值最小时，对应的两个参数值，即得到了线性函数。

算法三要素：

1）设置线性函数，即假设函数(Hypothesis)；

2）选定损失函数 J，

3）梯度下降，找到使得J值最小时，对应的theta_0, theta_1。

J值最小，预测的h_theta(x)值就会越接近标签纸y

3. 梯度下降：

找损失函数的最小值，高数知识可知对函数求导等于零，对应的点即为极值点，但不一定是最小值，可能是极小值（局部最小）或是极大值（极大值的倒数也为0）或拐点（参考高数课本）。但有些函数不能直接求出倒数值，所以需要梯度下降逐渐的趋向最小值。

梯度下降过程如下所示，便于分析，这里假设线性函数为 theta_1 * x, 没有 theta_0，theta = theta - alpha * K, K即为斜率，迭代变化\theta_1值，使得J值为0

其中，迭代过程：

4. Matlab实现：

clc;
clear;
data = load('D:/Code/Data/ex1data1.txt');
X = data(:,1);
y = data(:,2);
figure,
plot(X, y, 'r*', 'MarkerSize', 5); % 5控制*的大小

% x加了一列,变成 (97,2)
m = length(y); 
X = [ones(m, 1), data(:,1)]; 

% 初始化参数
theta = zeros(2, 1);

% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
% 梯度下降，找到最佳参数
theta = gradientDescent(X, y, theta, alpha, iterations);

hold on; 
% keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off

function theta = gradientDescent(X, y, theta, alpha, num_iters)

m = length(y); 
% 样本数量

for iter = 1:num_iters
    H = X * theta;
    %(97,2)*(2*1)=(97,1)
    Sum = [0 ; 0]; %(2,1)，记录偏导，求和
    
    % theta_0更新
    for i = 1 : m
        Sum(1,1) = Sum(1,1) + (H(i) - y(i));    
    end
    
    % theta_1更新
    for i = 1 : m
        Sum(2,1) = Sum(2,1) + (H(i) - y(i)) * X(i,2)';   
    end

    theta = theta - (alpha * Sum) / m;

end
end

关键代码：

    Sum = [0 ; 0]; %(2,1)，记录偏导，求和
    
    % theta_0更新
    for i = 1 : m
        Sum(1,1) = Sum(1,1) + (H(i) - y(i));
    end
    
    % theta_1更新
    for i = 1 : m
        Sum(2,1) = Sum(2,1) + (H(i) - y(i)) * X(i,2)';
    end
    
    theta = theta - (alpha * Sum) / m;

5. 效果如下：

二，多变量的线性回归

1. 多变量的例子，如下

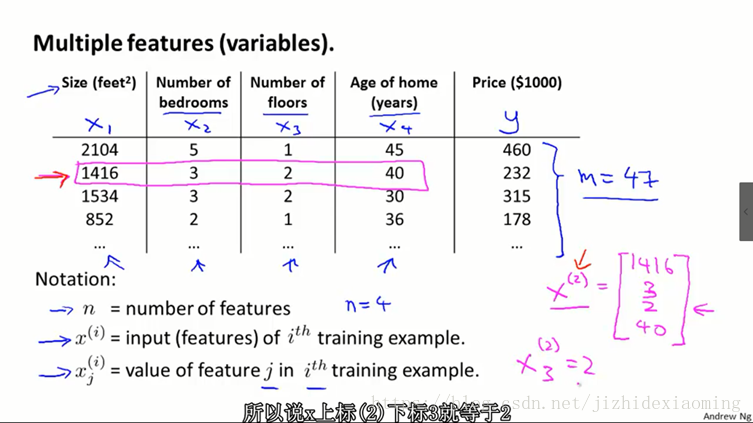
2. 数据集下载点击打开链接，密码：ibtb：

画出数据分布：

3. 多变量的假设函数定义：

4. 多变量的损失函数：

5. 迭代过程如下：

手推一把：

6. 多变量的线性回归，Matlab实现：

clear;
clc;

% 1，读取数据
x = load('D:\Code\Data\ex3Data\ex3x.dat'); % 两个变量房子面积，和卧室数目，一行一个样本
y = load('D:\Code\Data\ex3Data\ex3y.dat'); % 房子价格
% plot3(x(:,1), x(:,2), y, 'r*');
% grid on % 画上网格
% hold on; % 后面将画上拟合的线

% 2, 处理数据
m = length(x(:,1)); % 样本数
x = [ones(m,1), x]; % x0 为1
x(:,2) = (x(:,2) - mean(x(:,2))) ./ std(x(:,2));
x(:,3) = (x(:,3) - mean(x(:,3))) ./ std(x(:,3));
plot3(x(:,1), x(:,2), y, 'r*');
grid on % 画上网格
hold off;

% 3，参数设置
iter = 1500; % 迭代次数
theta = zeros(1,3); % 线性函数的参数，为行向量
alpha = 0.01;

J = zeros(m,1);
for i = 1:iter % 以迭代次数为终止条件
    
    % 求以当前theta为线性函数的参数时，其损失值
    h = x * theta'; % 假设函数
    J(i) = 1/2*m * sum((h - y).^2); % 记录每次迭代后损失值情况，但对迭代终止没有影响
    % 
    theta(1,1) = theta(1,1) - alpha*(1/m)* sum((h - y) .* x(:,1)); % x(:,1)即为x_0
    theta(1,2) = theta(1,2) - alpha*(1/m)* sum((h - y) .* x(:,2));
    theta(1,2) = theta(1,3) - alpha*(1/m)* sum((h - y) .* x(:,3));
    
%     theta = theta - alpha*(1/m)* sum(x'*(h - y)); % 一次性处理所有theta
    
end

figure,  % 画出损失函数随迭代次数的变化情况
plot(1:iter, J);

损失函数变化情况：

原文出处