插入排序
上节课我们学习了一个经典的排序算法—冒泡排序,本节我们来聊一下基础排序中的插入排序算法。
1. 插入排序算法原理
插入排序的基本思想是:将整个数组 nums 分为有序和无序的两个部分。前者在左边,后者在右边。最开始有序的部分只有第一个元素,其余都属于无序的部分。每次取出无序部分的第一个(最左边)元素,把它加入有序部分。通过比较找到属于该元素的位置 k,然后将原 k 位置及其后面的有序部分元素都向右移动一个位置,有序的部分即增加了一个元素,无序部分减少了一个元素。这样一直继续下去,直到无序的部分没有元素,整个插入排序就算完成。
2. 插入排序算法过程分析
下面我们用一个简单的图片描述下插入排序的过程,如下所示。

从上面的过程我们可以看到,比较关键的一步就是找到准备插入元素的位置。简单点的话,可以从有序部分的最后开始往前依次比较。若有序元素比该插入值大则该有序元素后退一个位置,然后继续向前比较,直到有序列表中的元素小于该插入值。

3. 插入排序算法的 Python 实现
看到前面的插入算法的思路有没有跃跃欲试,想赶紧把它写出来的冲动?先别急,我们先思考几个问题:
- 对于插入排序找到元素的插入位置,有没有可能利用有序的规律进一步优化算法?
- 插入排序的列表是链式的数据结构,我们是不是可以省掉移动元素这样一个比较耗时的部分?
我们现在分别实现3种情况下的插入排序算法:
- 普通的插入排序,从有序列表的最后依次往前查找插入元素的位置;
- 改进的插入排序,对于查找插入元素位置改为使用二分查找方法,然后统一移动插入元素后面的所有元素;
- 链表元素的插入排序;
3.1 普通的插入排序
我们直接看代码:
def insert_sort(nums):
"""
插入排序
"""
if not nums:
return False
for i in range(1, len(nums)):
t = nums[i]
# 从i-1位置开始往前找
for j in range(i - 1, -1, -1):
k = j
# 如果nums[j]大于t,继续向前,直到找到小于等于t的数
if nums[j] <= t:
k = k + 1
break
# 每次找到的nums[j]大于t,则将当前值想向移动一位
nums[j + 1] = nums[j]
# 此时找到t的位置,并将t放到对应位置
nums[k] = t
return True
看上面的代码,第二个 for 循环便是从有序列表的最后一个元素开始和待插入值进行比较,并逐步向前移动比较,一但待插入值大于或等于当前值,那么待插入值就在该值的后面位置插入;否则将当前位置的值向后移动一位,给待插入值腾出空间 (因此插入值必须一开始先保存,如果被最后一个值给覆盖了,该插入值就没了)。
4. 插入排序算法的优化
从上面的内容中可以很明显看出插入排序有一个可以优化的地方,就是插入排序中每次查找插入元素的位置时,我们可以利用前面已排好序的特点,使用二分法快速定位插入元素位置,这样会比从后向前一个一个比较要高效许多,特别是在排序规模较大时,尤为明显。
4.1 使用二分法的插入排序
二分法查找是一种非常高效的搜索方法,主要原理是每次搜索可以抛弃一半的值来缩小范围。其时间复杂度是O(log2n),一般用于对普通搜索方法的优化。使用二分法时一定要保证数组是排序的,例如下面的数组:
5 8 10 12 17 20 25 26
假设想查找 10 的位置,首先给个头尾指针:first 和 end,分别指向 0 和 7 的位置。取中间数 mid = (0 + 7) / 2 = 3 ,而 nums[3] = 12 > 10,可知 10 的位置肯定在 first 和 mid 指针之间。此时我们将 end = mid,然后继续使用前面那样的方式在左边数组中查找,直到最后 first >= end 为止。
在 Python 中有一个二分查找模块:bisect,该模块中的方法都是基于二分查找法,可以使用 bisect_right() 方法来辅助我们快速实现插入元素的定位。首先在 Python 的交互式模式下测试下该方法:
>>> from bisect import bisect_right
>>> x = [2, 3, 4, 7, 9, 12]
>>> bisect_right(x, 5)
3
>>> bisect_right(x, 1)
0
>>> bisect_right(x, 13)
6
>>> bisect_right(x, 7)
4
可以看到,bisect_right() 方法快速返回了待插入元素在有序列表中的位置。
注意:在 bisect.py 模块中,bisect_right() 方法又给了一个别名,就是 bisect:
# 源码位置:lib/bisect.py
# ...
# Create aliases
bisect = bisect_right
于是我们给出基于二分法的插入排序算法:
from bisect import bisect
def insert_sort2(nums):
"""
插入排序: 使用二分法实现元素快速插入
"""
if not nums:
return False
for i in range(1, len(nums)):
k = bisect(nums[:i], nums[i])
nums[k], nums[k + 1: i + 1] = nums[i], nums[k:i]
return True
可以看到,使用了二分模块之后,插入排序算法的代码变得非常简洁,而且也相比原来的代码高效了不少。大家可以把排序的规模弄到万级别上进行测试和对比,就能够看到代码的区别。
4.2 基于链表的插入排序
对于使用的链表结构的数据我们无法向前面那样使用二分法进行插入位置的获取,但这样的链表结构有一个好处,就是我们找到对应的插入位置后,后面的元素不用整体后移,只需要 O(1) 的复杂度即可插入成功。
我们就来实现一下这个基于链表的插入排序算法。首先是要分析链表插入的思路,来看初始的状态:
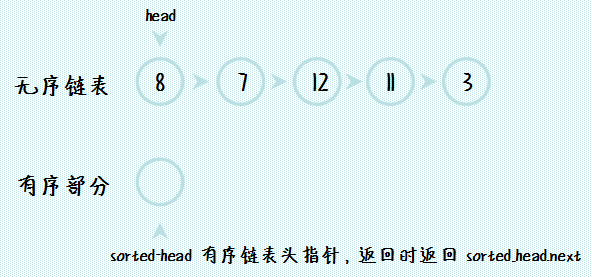
我们自定义一个有序链表的头部 head,这样是为了后面操作的方便。接下来每次从无序链表中选择一个数据插入到有序链表中,首先完成初始代码如下:
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def insertion_sort_list(head):
# 定义一个新的有序节点
new_sorted = ListNode(0)
p = head
while p:
# 每次插入值为p.val的节点
# ...
# 重新指向下一个待插入的数据
p = p.next
return new_sorted.next
可以看到,比较核心的代码就是对于有序链表,如何插入一个值并保证链表的有序。我们的有序链表插入过程如下,需要准备 prev 和 cur 两个指针,分别表示当前比较的值的位置和上一个元素的位置,来看看插入有序链表的示意图:
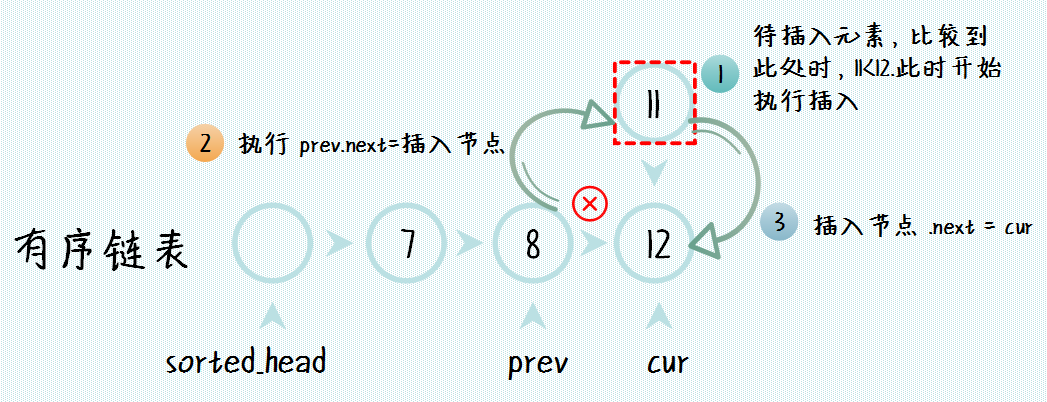
由于链表的单向性,我们需要从有序链表的第一个元素开始比较,直到找到元素值大于该插入节点的值,然后就需要执行插入动作。这里需要考虑两种极端情况,一种是插入到最前面,另一种是插入到最后面。完整的链表插入排序算法的代码如下(代码中已做好详细注释):
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def insert_link_sort(head):
sorted_head = ListNode(0)
p = head
while p:
prev = sorted_head
cur = prev.next
if not cur:
# 针对于第一次,第一个元素直接挂到sorted_head后即可
sorted_head.next = ListNode(p.val)
else:
find = False
while cur:
if p.val > cur.val:
# 插入节点值大于当前指向的节点值,将cur和prev之后后移一位再比较
cur = cur.next
prev = prev.next
else:
# 当前节点值大于插入元素的值,在此执行插入操作然后退出循环
insert_data = ListNode(p.val)
prev.next = insert_data
insert_data.next = cur
find = True
break
# 对于大于所有的值,需要插入到有序链表的末尾
if not find:
prev.next = ListNode(p.val)
p = p.next
return sorted_head.next
最后这个在 leetcode 上有一道对应的编程题,题号为147,难度标记为中等。我这里的代码并不优秀,只是看起来比较简单明了,额外用了许多空间。大家有兴趣的话可以优化下代码,实现在原链表的基础上完成插入排序。
5. 小结
本小节中,我们介绍了插入排序算法的排序原理及思路,同时分别完成了3种情况的插入排序算法,特别是最后一种情况的实现,涉及到链表操作,大家要多多练习,掌握这些基础的排序算法。
Tips:文中动图制作参考:https://visualgo.net/zh/sorting。