分治算法介绍
今天我们聊一聊计算机中非常重要和常用的一种算法:分治算法。它在计算机领域应用广泛,几乎无处不在。不仅计算机领域,在信号处理领域,分而治之也是十分常见的一种信号处理方法。著名快速傅里叶变换算法 (FFT) 正是使用了分而治之的思路,才使得数字信号处理算能广泛使用,这也才造就了我们今天丰富多彩的生活。
1. 分治算法思想
分而治之是计算机领域中非常重要的一种思想:即将大规模问题每次通过分解成小问题进行处理,在处理完小问题之后再将结果合并成大问题的最终结果。
2. 举例说明分治算法的典型应用
非常典型的一个示例是排序算法中的归并排序。假设我们要排序 8 个数,我们首先将 8 个数的列表分解成两个 4 个数的列表,一直划分下去直到列表中最多只有 2 个元素。接下来对所有的 2 个或者 1 个元素的列表进行排序,然后再两两合并,直到最后合并成最终长度为 8 的列表,则排序结束。其算法示意图如下所示:
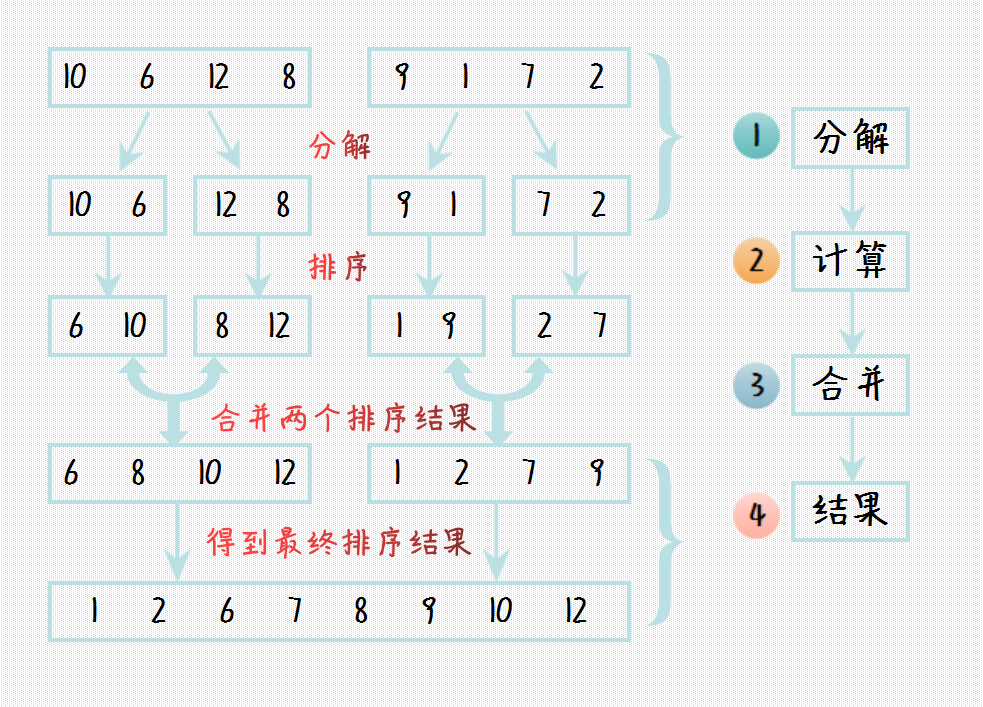
可以看到:归并排序中的一个核心步骤是对两个有序数组的合并过程,对此使用的合并算法过程如下图所示:
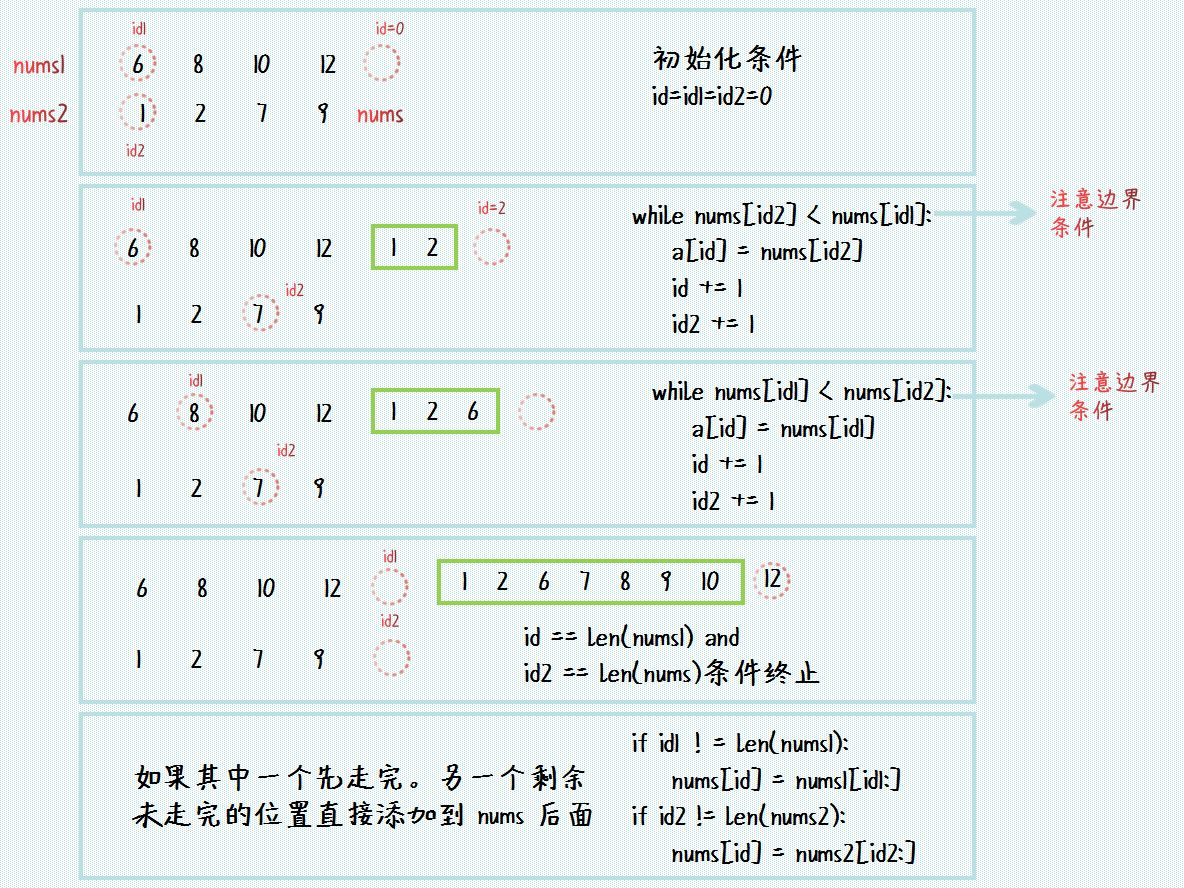
3. 分治算法的 Python 代码实现
有了上面的算法过程,我们就可以写出合并两个有序列表的代码,如下:
def merge_sorted_list(nums1, nums2):
"""
合并有序列表
"""
nums = [0] * (len(nums1) + len(nums2))
id, id1, id2 = 0, 0, 0
# 循环条件,当有一个等于数组长度时,终止
while id1 < len(nums1) and id2 < len(nums2):
# 对应着上图中第三个操作,多加了边界操作
while id1 < len(nums1) and id2 < len(nums2) and nums1[id1] <= nums2[id2]:
nums[id] = nums1[id1]
id += 1
id1 += 1
# 对应着上图第二个部分操作,多加了边界操作
while id1 < len(nums1) and id2 < len(nums2) and nums2[id2] < nums1[id1]:
nums[id] = nums2[id2]
id += 1
id2 += 1
# 对应于图片的最后部分,如果一个数组先走完,另一个数组剩余部分直接添加到新数组的最后
if id1 != len(nums1):
nums[id:] = nums1[id1:]
if id2 != len(nums2):
nums[id:] = nums2[id2:]
return nums
接下来从分解到合并这个过程是不是特别像递归?看看递归三要素应该怎么做,第一是终止条件,很明显在列表长度为 1 或者 2 时终止;第二是方法的返回值,可以是列表头,表示得到新的排序的列表;第三是递推公式,即将已经排好序的结果合并成完整的排序结果,用的正是上面的合并方法,这样我们就可以写出如下归并排序的代码:
def merge_sort(nums):
"""
递归终止条件
"""
if len(nums) == 1:
return nums
if len(nums) == 2:
if nums[0] > nums[1]:
nums[0], nums[1] = nums[1], nums[0]
return nums
# 递归公式,将列表平均分成两份,然后递归排序下去
half = len(nums) // 2
nums1 = merge_sort(nums[:half])
nums2 = merge_sort(nums[half:])
# 调用合并操作,得到最终结果
return merge_sorted_list(nums1, nums2)
从上面的排序算法示例中我们可以看到典型分治算法的解题步骤如下:
- 分解:要解决的问题划分成若干规模较小的同类问题;
- 求解:当子问题划分得足够小时,可以采用已有或者简单的算法解决;
- 合并:再得到每个子问题的解后,还需要将这些结果合并成最后大问题的结果,这才是最终答案。
4. 另一个分而治之的应用介绍
另一个分治算法的典型应用是大整数相乘问题。对于两个以字符串形式表示的长整数,计算其相乘结果。关于分治法比较核心的一个问题就是,找到如何将子问题的解合并成父问题的解。我们简单描述一下这个基于分治思想的大数乘法算法,又叫 Karatsuba 算法。
假设 x 和 y 是两个要做乘法的十进制大数,并且位数分别为 m 和 n。若将 x 和 y 分别均分成两部分,则 x 和 y 可以表示如下:
此时有:
这样大整数乘法就被分解成 4 个长度减半的整数的乘法。如此执行下去,直到执行的乘法的两数足够小时,然后计算反推最终结果。根据上面的执行思路,我们开始一步一步得到大整数相乘的分治代码。
首先处理初始以及最后分治的终止条件:如果 s1 或者 s2 中有一个为空串,那么相乘结果为 '0‘,注意输出字符串;此外,分解到最后 s1 和 s2 字符串的长度均为1 时,我们可以直接将两个字符串强装成数字然后进行相乘,最后返回的结果也要再转成字符串:
if not s1 or not s2:
# 有一个为空,则结果为0
return '0'
elif len(s1) == 1 and len(s2) == 1:
# 终止条件
return str(int(s1) * int(s2))
接下来开始对字符串 s1 和 s2 进行分治求解:
# 其余情况
l1 = len(s1) // 2
l2 = len(s2) // 2
# 将s1分成两部分
a = s1[:l1]
b = s1[l1:]
# 将s2分成两部分
c = s2[:l2]
d = s2[l2:]
接下来我们分别得到了4个子串:a、b、c、d。按照前面的公式,我们分别要计算 ac、bc、ad 和 bd 的值。这些值可以使用递归方法得到,要注意相乘结果的10次幂需要保留,以便后续能合成最终问题的解。
mi = len(b) # 对于a的10次幂
ni = len(d) # 对于c的10次幂
# 分别计算ac, ad, bc, bd,分别补上相应的幂次,使用分治计算
x1 = bigDataMultiple(a, c) + '0' * (mi + ni)
x2 = bigDataMultiple(a, d) + '0' * mi
x3 = bigDataMultiple(b, c) + '0' * ni
x4 = bigDataMultiple(b, d)
最后是计算 x1+x2+x3+x4 的值便可得到原大问题的解,由于 x1~x4 均为字符串,我们按照字符串上每位数字相加来进行。首先需要将所有字符串的长度统一,对于短字符串需要将前面补零:
max_len = max(len(x1), len(x2), len(x3), len(x4))
x1 = '0' * (max_len - len(x1)) + x1
x2 = '0' * (max_len - len(x2)) + x2
x3 = '0' * (max_len - len(x3)) + x3
x4 = '0' * (max_len - len(x4)) + x4
接着从字符串最后一位开始,计算每位上的值,注意进位问题即可:
res = ''
c = 0
for i in range(max_len - 1, -1, -1):
s = int(x1[i]) + int(x2[i]) + int(x3[i]) + int(x4[i]) + c
res = str(s % 10) + res
c = s // 10
# 注意,如果循环完后进位>0,需要补上进位值
if c > 0:
res = str(c) + res
然而,通过提交代码发现有时候在合成最终结果时,字符串前面会出现 ‘0’。因此下面的代码就是找到前面非 ‘0’ 开头字符的位置:
# 去掉res最前面的'0'
k = 0
while res and k < len(res) and res[k] == '0':
k += 1
最后得到大整数相乘的最终结果为:res[k:]。
综合前面的分析与讨论,得到完成的处理大整数相乘问题的 Python 实现如下:
def bigDataMultiple(s1, s2):
"""
计算 s1 * s2,返回大整数相乘结果
"""
if not s1 or not s2:
# 有一个为空,则结果为0
return '0'
elif len(s1) == 1 and len(s2) == 1:
# 终止条件
return str(int(s1) * int(s2))
# 其余情况
l1 = len(s1) // 2
l2 = len(s2) // 2
# 将s1分成两部分
a = s1[:l1]
b = s1[l1:]
# 将s2分成两部分
c = s2[:l2]
d = s2[l2:]
mi = len(b) # 对于a的10次幂
ni = len(d) # 对于c的10次幂
# 分别计算ac, ad, bc, bd,分别补上相应的幂次,使用分治计算
x1 = bigDataMultiple(a, c) + '0' * (mi + ni)
x2 = bigDataMultiple(a, d) + '0' * mi
x3 = bigDataMultiple(b, c) + '0' * ni
x4 = bigDataMultiple(b, d)
# 将计算的结果根据最长的补零,方便后面直接相加计算
max_len = max(len(x1), len(x2), len(x3), len(x4))
x1 = '0' * (max_len - len(x1)) + x1
x2 = '0' * (max_len - len(x2)) + x2
x3 = '0' * (max_len - len(x3)) + x3
x4 = '0' * (max_len - len(x4)) + x4
# 计算x1+x2+x3+x4的值,也就是原问题的解
res = ''
c = 0
for i in range(max_len - 1, -1, -1):
s = int(x1[i]) + int(x2[i]) + int(x3[i]) + int(x4[i]) + c
res = str(s % 10) + res
c = s // 10
# 注意,如果循环完后进位>0,需要补上进位值
if c > 0:
res = str(c) + res
# 去掉res最前面的'0'
k = 0
while res and k < len(res) and res[k] == '0':
k += 1
return res[k:]
这道题是牛客网上的原题,我实现的分治算法略微复杂,大家可以参考上面的一些题解,有非常精简和高效的实现。多参考优秀的代码对我们提升自己编程能力也是有莫大好处的。
5. 分治法的时间复杂度分析
分治法的时间复杂度可以这样来分析,假设对于规模为 n 的问题,其直接计算的复杂度为 。那么我们看一下分解成 2 个子问题后其复杂度如何?我们以前面的归并排序的为例,如果是采用前面的选择排序、冒泡排序,算法的复杂度为 ,我们将其分解成两个 长度的列表进行排序后再合并,这样一次分解的时间复杂度为:
注意:后面的 n 为合并方法的时间复杂度。如果问题规模 n 非常大,此时一次分解再合并后的时间复杂度相比原算法少了一半,如果我们再次分解问题规模呢?
可以看到再次减少大约一半的计算量!!!如果原问题的复杂度是 甚至 ,那么使用分治算法能明显改进原算法性能,当前前提是该算法能进行分治求解。对于前面归并排序问题,其平均的时间复杂度最终可以达到 。
6. 小结
本小节我们使用两个典型的例子对分治算法的原理以及算法实现步骤进行了相应的说明,通过这两个简单的例子我们能体会分治算法的特点:简单高效。接下来我们会用更多 leetcode 习题来帮助我们巩固这一节所学的算法。