-

- libigfat 2020-06-27
scipy optimize 下面的优化器
minimize最小值
nelder-mead是一种计算最小值的方法
- 0赞 · 0采集
-

- 慕设计3172499 2019-07-25
#2-Optimizer from scipy.optimize import minimize def rosen(x): #hansu return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1]**2.0)) x0=np.array([1.3,0.7,0.8,1.9,1.2]) res = minimize(rosen,x0,method="nelder-mead",options={"xtol":1e-8,"disp":True}) print("ROSE MINI:",res.x) def func(x): return -(2*x[0]*x[1]+2*x[0]-x[0]**2-2*x[1]**2) def func_deriv(x): dfdx0 = -(-2*x[0] + 2*x[1] + 2) dfdx1 = -(2*x[0] - 4*x[1]) return np.array([dfdx0,dfdx1]) cons = ({"type":"eq","fun":lambda x:np.array([x[0]**3.0-x[1]]),"jac":lambda x:np.array([3.0*(x[0]**2.0),-1.0])}, {"type":"ineq","fun":lambda x:np.array([x[1]-1]),"jac":lambda x:np.array([0.0,1.0])}) res=minimize(func,[-1.0,1.0],jac = func_deriv,constraints=cons,method='SLSQP',options = {'disp':True}) print("RESTRICT:",res) from scipy.optimize import root def fun(x): return x+2*np.cos(x) sol=root(fun,0.1) print ("ROOT:",sol.x,sol.fun)有结果不对的可以自己比对一下,视频可能有点模糊和拖动
- 0赞 · 0采集
-

- qq_慕娘1462895 2019-04-29
**2. 优化(scipy.optimize)**
scipy.optimize模块提供了函数最值、曲线拟合和求根的算法。
该模块包括:
——多元标量函数的无约束和约束极小化(minimize)。使用多种算法(例如BFGS、Nder-Mead单纯形、Newton共轭梯度、COBYLA或SLSQP)
——全局(蛮力)优化例程。basinhopping, differential_evolution)
——最小二乘极小化(least_squares)和曲线拟合(curve_fit)算法
——标量单变量函数极小化(minimize_scalar)和根查找器(root_scalar)
——多元方程组求解器(root)使用多种算法(例如,混合鲍威尔、Levenberg-MarQuardt或大规模方法,如Newton-Krylov)
**无约束函数最值(以最小值为例):**
导入模块:
```
from scipy.optimize import minimize
import numpy as np
```
在数学最优化中,Rosenbrock函数是一个用来测试最优化算法性能的非凸函数,由Howard Harry Rosenbrock在1960年提出。也称为Rosenbrock山谷或Rosenbrock香蕉函数,也简称为香蕉函数。
函数表达式(N是x的维数):
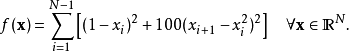
定义一个目标函数(Rosenbrock函数——香蕉函数):
```
def rosen(x):
"""The Rosenbrock function"""
return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0+(1-x[:-1])**2.0)
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
```
求解:
```
res = minimize(rosen, x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})
print(res.x) #res.x是优化结果,返回一个ndarry
```
minimize(fun, x0[, args, method, jac, hess, …])
fun——一个或多个变量的标量函数的最小化
x0——初始猜测值,相当于指定了N
method就是优化算法
Xtol是精度
disp指是否显示过程(True则显示)
过程与结果:
```
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 339
Function evaluations: 571
[1. 1. 1. 1. 1.]
```
**有约束函数最值(最小值为例):**
导入模块:
```
from scipy.optimize import minimize
import numpy as np
```
定义函数:
f(x) = 2xy+2x-x^2^-2y^2^
偏导数:
2y+2-2x
2x-4y
```
def fun(x):
return (2*x[0]*x[1]+2*x[0]-x[0]**2-2*x[1]**2)
def func_deriv(x):
dfdx0 = (-2*x[0]+2*x[1]+2)
dfdx1 = (2*x[0]-4*x[1])
return np.ndarry([dfdx0,dfdx1])
```
约束条件(等于转化为=0和不等于转化为>=0):
3x^2^-y = 0
y-1>=0
```
cons = ({"type":"eq","fun":lambda x;np.ndarray([x[0]**3-x[1]]),"jac":lamda x;np.ndarray([3*(x[0]**2),-1])}
,{"type":"ineq","fun":lambda x;np.ndarray([x[1]-1]),"jac":lamda x;np.ndarray(0,1])})
```
雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。
求解:
```
x0 = np.array([-1.0, 1.0])
>>> res = minimize(func, x0, method='SLSQP', jac=func_deriv,constraints=cons, options={'disp': True}) #顺序最小二乘规划(SLSQP)算法(method='SLSQP')
print(res.x)
```
结果:
```
x:array([1.0000009,1])
```
**优化器求根:**
导入模块:
```
from scipy.optimize import root
import numpy as np
```
定义函数:
x+2cos(x) = 0
```
def func(x):
return x + 2 * np.cos(x)
```
求解和结果:
```
sol = root(func, 0.1) #root(fun,x0),fun为函数,x0是Initial guess.(初始猜测值)
print(sol.x) #优化(根)结果
>>array([-1.02986653])
print(sol.fun) #目标函数的值
>>array([ -6.66133815e-16])
```
- 4赞 · 0采集


