-

- 慕仔6547137 2021-02-02
- 看不懂怎么回事……
- 0赞 · 0采集
-

- 慕斯8442767 2020-11-06
线性回归算法
矩阵算法、梯度算法

- 0赞 · 0采集
-

- 慕斯8442767 2020-11-05
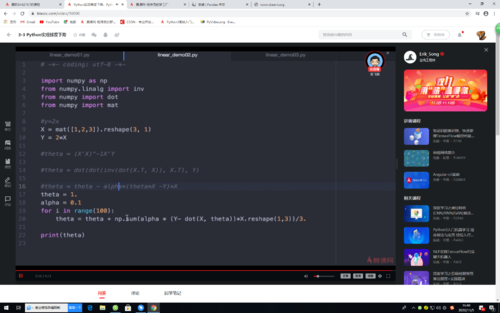
梯度下降法计算
- 0赞 · 0采集
-

- 慕斯8442767 2020-11-05
矩阵的操作

- 0赞 · 0采集
-

- weixin_慕的地2302707 2020-05-14
矩阵A,B的点成:np.dot(A,B)
- 0赞 · 0采集
-

- weixin_慕的地2302707 2020-05-14
矩阵B的逆:np.inv(B)
- 0赞 · 0采集
-

- weixin_慕的地2302707 2020-05-14
矩阵A的转置:A.T
- 0赞 · 0采集
-

- 慕前端5077229 2020-03-09
最小二乘法模型
-
截图0赞 · 0采集
-

- jingleYao 2020-02-17
梯度下降函数
-
截图0赞 · 0采集
-

- jingleYao 2020-02-17
直接运算的问题
矩阵需要满秩
运算性能
-
截图0赞 · 0采集
-

- jingleYao 2020-02-17
最小二乘法模型
-
截图0赞 · 0采集
-

- jingleYao 2020-02-17
线性回归的数学表示
-
截图0赞 · 0采集
-

- 霜花似雪 2019-10-26
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
import numpy as np from numpy.linalg import inv from numpy import dot from numpy import mat if __name__ == "__main__": # 训练数据 x = mat([1, 2, 3]).reshape(3, 1) # 1行3列转化为3行1列 y = 2 * x #梯度下降: # 原理:多次更新theta的值,通过theta与x,y的关系来得到theta # theta = theta - alpha*(theta*x-y)*x (alpha取值为0到1,保证梯度下降的变化速率不要太快,在一个合适的区间之内,使得函数迅速收敛,找到局部最小值) theta = 1.0 #初始化theta alpha = 0.1 #初始化alpha for i in range(100): theta = theta + np.sum(alpha * (y - dot(x, theta)) * x.reshape(1, 3))/3 # np.sum 求加权平均值 print(theta)
- 0赞 · 0采集
-

- 霜花似雪 2019-10-26
import numpy as np from numpy.linalg import inv from numpy import dot from numpy import mat if __name__ == "__main__": A = np.mat([1, 1]) # 1行2列的矩阵 print('A:\n', A) Arr = np.array([1,1]) #数组 print("Arr:\n",Arr) #A矩阵是1*2转化为2*1 print("A矩阵转化2行1列:", A.reshape(2, 1)) # A矩阵转置 print('A.T:\n', A.T) # 1行2列 转置为 2行1列 print("-------------------------") B = mat([[1,2],[2,3]]) #2*2的矩阵 print('B:\n',B) #求B矩阵的逆矩阵 print('B的逆矩阵:\n', inv(B)) #获取B矩阵的第一行 print("B矩阵的第一行",B[0, :]) #第一行所有列 #获取B矩阵的第一列 print("B矩阵的第一列:", B[:, 0]) #所有行第一列 print("B矩阵转化为1行4列:\n", B.reshape(1, 4)) # A: 1*2 B: 2*2 print('A*B:\n', dot(A,B)) # A.T 2*1 B:2*2 print('B*A:\n', dot(B,A.T)) #B矩阵*A的转置矩阵- 0赞 · 0采集
-

- 霜花似雪 2019-10-26
梯度下降算法
-
截图0赞 · 0采集
-

- 霜花似雪 2019-10-26
直接计算的问题
-
截图0赞 · 0采集
-

- 霜花似雪 2019-10-26
最小二乘法模型
向量表示
Y=θX,θ和X是矩阵
L=1/2(θX-Y)^T(θX-Y)
第二行为损失函数(欧几里得距离/向量中向量空间的距离)
//这个损失函数是线性的,而神经网络的损失函数是非线性的
-
截图0赞 · 0采集
-

- 霜花似雪 2019-10-26
线性回归的数据表示
-
截图0赞 · 0采集
-

- 霜花似雪 2019-10-26
什么是线性回归
y~x :y与x是一对一的关系,映射到几何上就是二维坐标系中的直线方程
Y = θX
通过训练,得到θ的过程,就是线性回归算法。
其中:x是输入,y是输出,是结果
-
截图0赞 · 0采集
-

- 奶思奈斯 2019-08-25
12345
-
截图0赞 · 0采集
-

- 编程鬼才的学徒 2019-06-16
那么总的来说梯度下降是为了优化线性回归运行代码的运算性能和简洁化来实现的,那线性回归的最终效果对于算法,机器学习,甚至是人工智能会起到怎样的作用?
线性回归在算法和机器学习里所占比重是多少?还是说线性回归是机器学习不可或缺的一个算法?为了提高严谨性么?
- 0赞 · 0采集
-

- 编程鬼才的学徒 2019-06-16
dfjdifjdifjidjif
- 0赞 · 0采集
-

- qq_黄蓉_0 2019-06-13
线性回归的数学表示:

- 0赞 · 0采集
-

- 曹文 2019-06-08
- y=kx 线性回归,通过训练得到k的过程,就称为线性分析
-
截图0赞 · 0采集
-

- XuNeverStop 2019-01-13
最小二乘法模型
A=(seta*x-y) (A为一维列向量)
L=1/2*A^2 = (seta*x-y)^T (seta*x-y)=x^T*seta^T*seta*x-x^T*setaT*y-y^T*seta*x+y^T*y
L对seta求偏导:1/2*{x^T*x*[seta+(seta^T)^T] - x^T*y - (y^T*x)^T}=1/2[2*x^T*x*seta - 2*x^T*y] = x^T*x*seta - x^T*y
令L'=0有seta = (x^T*x)^-1*(x^T*y)
所以当seta = (x^T*x)^-1*(x^T*y)时L最小
-
截图0赞 · 0采集
-

- 左玉晶 2018-12-10
import numpy as np
from numpy.linalg import inv——(矩阵的逆)
from numpy import dot——(矩阵的点成)
from numpy import mat——(矩阵)
A=np.mat([1,1])——(1x2 的矩阵)
print('A:\n',A)
#A=np.array([1,1])——(数组)
B=mat([1:2],[3:4])——(2x2的)
print('B:\n',B)
print(''A.B:',dot(A,B))——结果是错的,因为1*2和2*2矩阵是不能想乘的
那么就需要给A矩阵转置:print('A.T:\n',A.T)
还有对矩阵B求逆:print('B的逆:\n',inv(B))
print(B[0,:1])——表示取出0行一列
print(B[:,0])——表示取出的是所有行第一列,就是第一列
print(A.reshape(2,1))——就是重新改变A矩阵的大小的,变成2*1的了;它不仅可以像转置一样还可以将3*2的变成1*6的,这是转置办不到的!
以上矩阵的基本操作:
接下来是线性回归的计算:
imort numpy as np
from numpy.linalg import inv
from numpy import dot
from numpy import mat
#计算y=2x
x=mat([1,2,3]).reshape([3,1])
y=2*x
#再计算theta=(x'x)^-1x'y
theta=dot(dot(inv(dot(x.T,x)),x.T),y)
print(theta)
接下来是梯度下降的算法:
(就是根据Y与X的关系不断的进行迭代计算)
#theta=theta-alpha*(theta*X-Y)*X——alpha在(0,1)之间取值,保证下降的梯度不会太快,是函数迅速收敛,是很重的学习内容
theta=1.
alpha=0.1
for i in range(100):
theta=theta+np.sum(alpha*(Y-dot(X,theta))*X.reshape(1,3))/3.——bp.sum()可以进行加权平均,因为X是3组数,而结果theta就是一个数,所以加权平均一下,结尾出“/3.”是除以其组数
(梯度下降是逐步逼近那个值的)
接下来完成一个复杂的线性回归l:
【
import random
def Y(X1, X2, X3):
return 0.65 * X1 + 0.70 * X2 - 0.55 * X3 + 1.95
def Produce():
filename = 'data.csv'
with open(filename, 'w') as file:
file.write('Unnamed: 0,Y,X1,X2,X3\n')
for i in range(150):
random.seed()
x1 = random.random() * 10
x2 = random.random() * 10
x3 = random.random() * 10
y = Y(x1, x2, x3)
try:
file.write(str(i)+','+ str(y)+ ',' +str(x1) + ',' + str(x2) + ',' + str(x3) + '\n')
except Exception as e:
print ('Write Error')
print (str(e))
Produce()
】
- 1赞 · 0采集
-

- 滕玉龙 2018-12-08
梯度下降方法(第二种代码)可以很好地解决向量方法(第一种)面对大量计算无法计算的弊端
而梯度下降更重要的是进行同步更新
所以需要一个temp来进行缓存
注意矩阵的形式可能需要变形——
reshape( )(如果出错,改成values.reshape( ))
- 0赞 · 0采集
-

- 滕玉龙 2018-12-08
>>> import numpy as np
>>> from numpy.linalg import inv
>>> from numpy import dot
>>> from numpy import mat
>>> import pandas as pd
>>> dataset=pd.read_csv('data.csv')
>>> print(dataset)
- 0赞 · 0采集
-

- 滕玉龙 2018-12-08
temp=dataset.iloc[:,2:5]
读取数据方法——定义了一个函数 iloc()
temp = dataset.iloc[:,2:5]
把X读出来
temp['x0']=1
偏移
X=temp.iloc[:,[3,0,1,2]]
显示顺序 第3列 第0列 第1列 第2列
- 0赞 · 0采集
-

- 滕玉龙 2018-12-08
回归分析实战
import numpy as np
from numpy.linalg import inv
from numpy import dot
from numpy import mat
import pandas as pd;
- 0赞 · 0采集












