了解红黑树的起源，理解红黑树的本质

你好，我是彤哥。

前面两节，我们一起学习了关于跳表的理论知识，并手写了两种完全不同的实现，我们放一张图来简单地回顾一下：

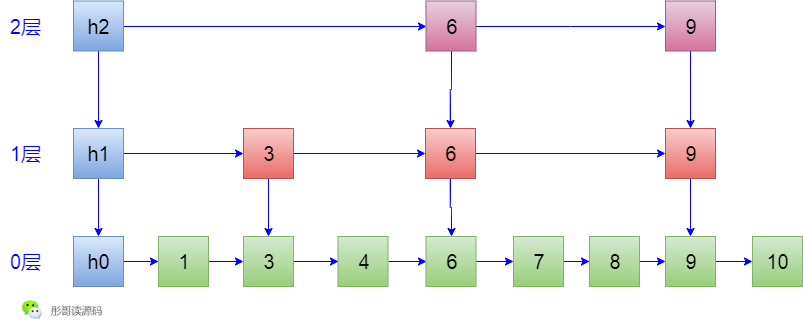
实现跳表的关键之处是在有序链表的基础上加上各层索引，通过这些索引可以做到O(log n)的时间复杂度快速地插入、删除、查找元素。

说起跳表，我们就不得不提另一种非常经典的数据结构——红黑树，红黑树相对于跳表来说，虽然时间复杂度都是O(log n)，但是红黑树的使用场景相对更广泛一些，在早期的Linux内核中就一直存在红黑树的实现，也运用在了更高效的多路复用器Epoll中。

所以，红黑树是每一个程序员不得不会的知识点，甚至有些变态的面试官，还会让你手写红黑树的一部分实现，比如左旋、右旋、插入平衡的过程、删除平衡的过程，这些内容非常复杂，靠死记硬背往往很难彻底掌握。

彤哥也是一直在寻找一种红黑树的记忆法，总算让我找到了那么一种还算不错的方式，从红黑树的起源出发，理解红黑树的本质，再从本质出发，彻底掌握不用死记硬背的方法，最后再把它手写出来。

从本节开始，我也将把这种方法传递给你，因此，红黑树的部分，我会分成三个小节来讲解：

• 从红黑树的起源，到红黑树的本质
• 从红黑树的本质，找到不用死记硬背的方法
• 不靠死记硬背，手写红黑树

好了，下面我们就进入第一小节。

红黑树的起源

二叉树

说起树，我们不得不说最有名的树，那就是二叉树，什么是二叉树呢？

二叉树（binary tree），是指树中的每个节点最多只有两个子节点的树。

当然，二叉树本身似乎没什么用，我们平时说的二叉树基本上都是指二叉查找树，或者叫有序二叉树、二叉搜索树、二叉排序树。

二叉查找树

二叉查找树（BST，binary search tree），就是在二叉树的基础上增加有序性，这个有序性一般是指自然顺序，有了有序性，我们就可以使用二叉树来快速的查找、删除、插入元素了。

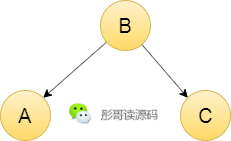
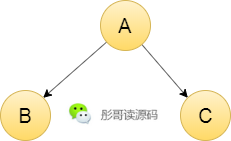
比如，上面这颗二叉查找树，查找元素的平均时间复杂度为O(log n)。

但是，二叉查找树有个非常严重的问题，试想，还是这三个元素，如果按照A、B、C的顺序插入元素会怎样？

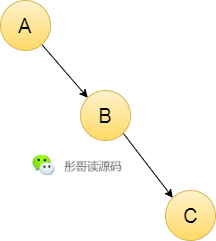
这是啥？单链表？没错，当按照元素的自然顺序插入元素的时候，二叉查找树就退化成单链表了，单链表的插入、删除、查找元素的时间复杂度是多少？O(n)。

所以，在极限情况下，二叉查找树的时间复杂度是非常差的。

既然，插入元素后有可能导致二叉查找树的性能变差，那么，我们是否可以增加一些手段，让插入元素后的二叉查找树依然性能良好呢？

答案是肯定的，这种手段就叫做平衡，这种可以自平衡的树就叫做平衡树。

平衡树

平衡树（self-balancing or height-balanced binary search tree），是指插入、删除元素后可以自平衡的二叉查找树，使得它的时间复杂度可以一直渐近于O(log n)。

比如，上面那颗树，按A、B、C插入元素后，做一次旋转操作，就可以再次变成查找时间复杂度为O(log n)的树。

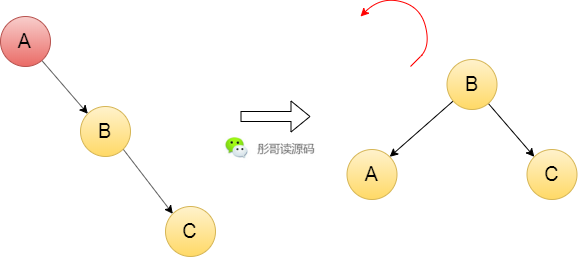
但是，平衡树一直只是一个概念，直到1962年才由两个苏联人发明了第一种平衡树——AVL树。

严格来说，平衡树是指可以自平衡的二叉查找树，三个关键词：自平衡、二叉、查找（有序）。

AVL树

AVL树（由发明者Adelson-Velsky 和 Landis 的首字母缩写命名），是指任意节点的两个子树的高度差不超过1的平衡树。

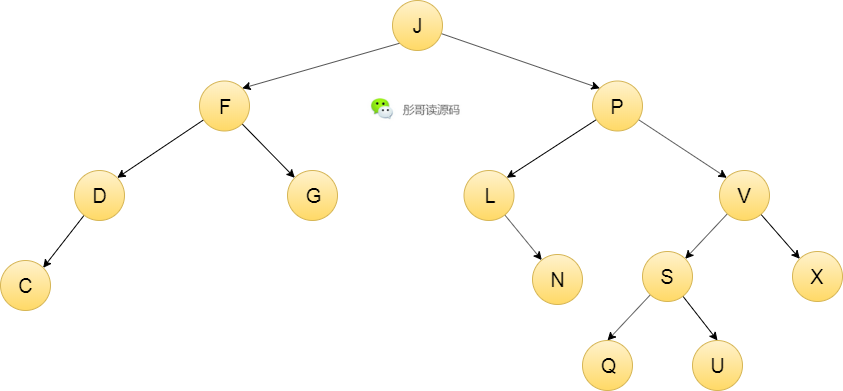
比如，上面这颗树，就是一颗AVL树，不信你可以数数看，是不是每个节点的两个子树的高度差都不超过1。

是不是很难发现它真的是一颗AVL树，没错，这是AVL树的第一个缺点，不够直观，特别是节点个数多的时候。

第二个缺点，就是插入、删除元素的时候自平衡的过程非常复杂，比如，上面这颗树插入一个节点T：

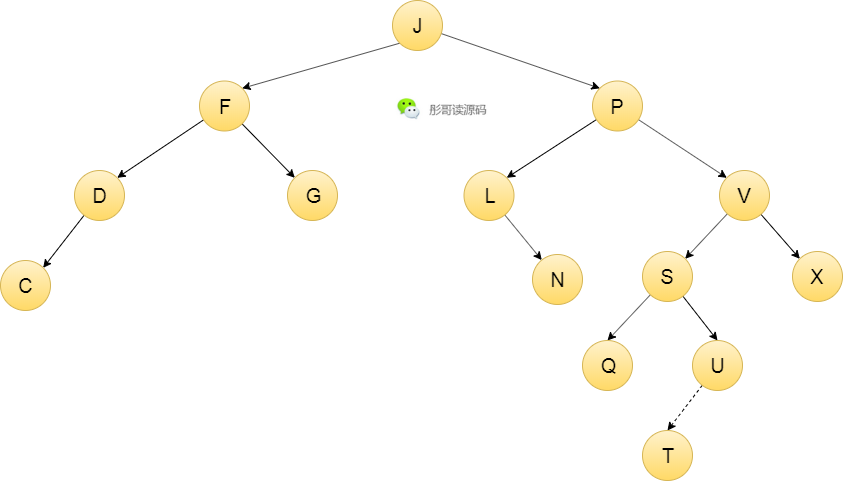
我们从T往上找，它的父节点U，U的两颗子树的高度差为1，满足AVL树的规则，再往上，S的两颗子树的高度差为1，也满足规则，再往上，V的两颗子树的高度差为2，不满足规则，此时，需要一个自平衡的过程，该如何自平衡呢？

我下面给出图示，你可以试着理解一下：

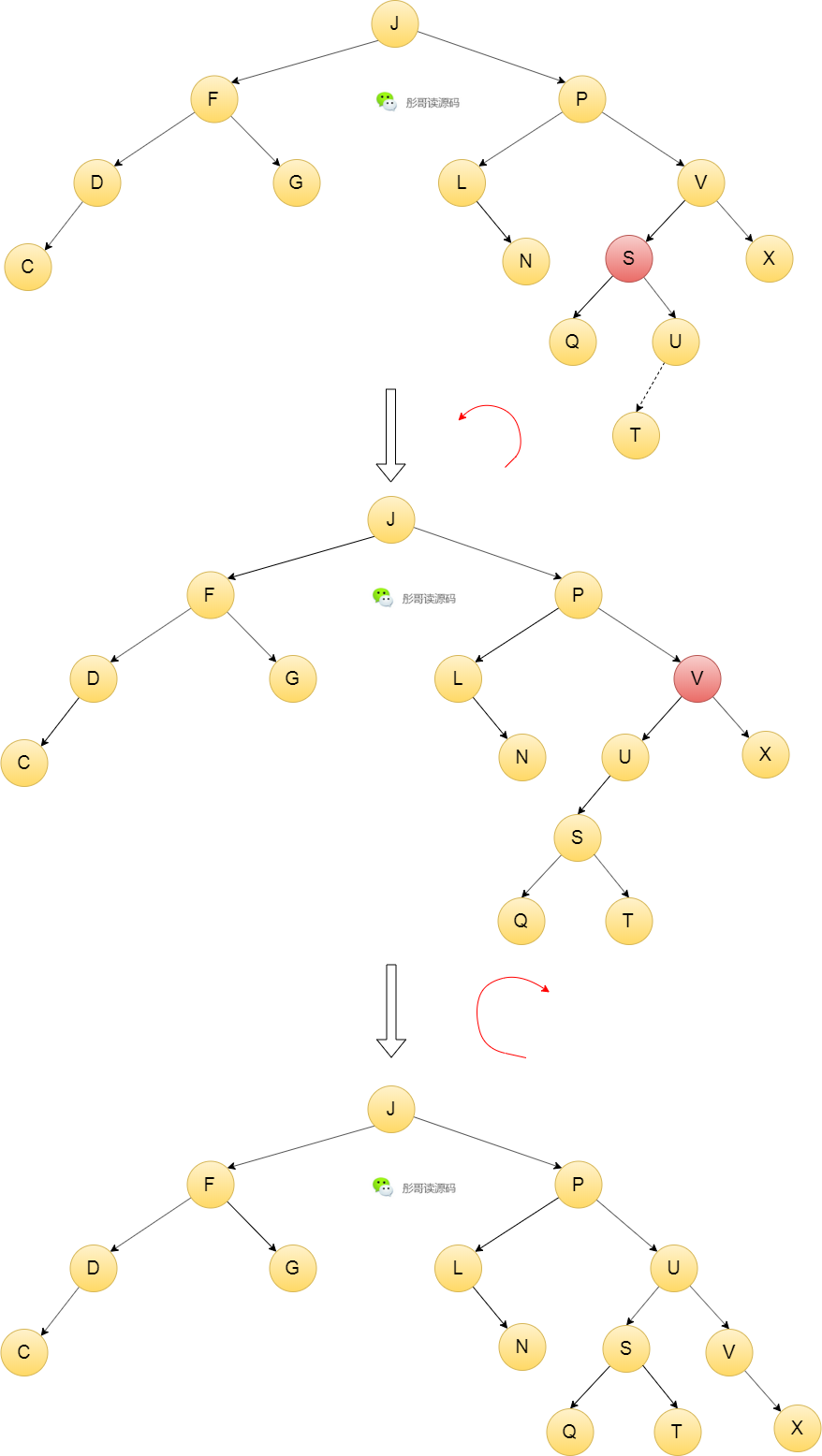
红色节点表示旋转的轴。

经过两次旋转，让这颗树再次变成了AVL树，而且这只是其中一种插入场景，真实的情况还要根据插入的位置的不同做不同的旋转，你可以多插入几个节点自己尝试平衡一下。

同样地，AVL树的代码也不是那么好实现的，反正，到目前为止，彤哥是没搞懂AVL树的各种规则。

基于这些缺点，所以，后来又发展出来了各种各样的神奇的平衡树。

2-3树

2-3树，是指每个具有子节点的节点（内部节点，internal node）要么有两个子节点和一个数据元素，要么有三个子节点和两个数据元素的自平衡的树，它的所有叶子节点都具有相同的高度。

简单点讲，2-3树的非叶子节点都具有两个分叉或者三个分叉，所以，称作2叉-3叉树更容易理解。

另外一种说法，具有两个子节点和一个数据元素的节点又称作2节点，具有三个子节点和两个数据元素的节点又称作3节点，所以，整颗树叫做2-3树。

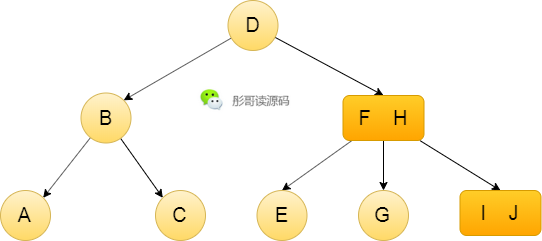
2-3树，插入元素后自平衡的过程相对于AVL树就要简单得多了，比如，上面这颗树，再插入一个元素K，它会先找到I J这个节点，插入元素K，形成临时节点I J K，不符合2-3树的规则，所以分裂，J往上移，F H这个节点变成了F H J了，也不符合2-3树的规则，继续上移H，根节点变为D H，同时，上移的过程中，子节点也要相应的分裂，过程大致如下：

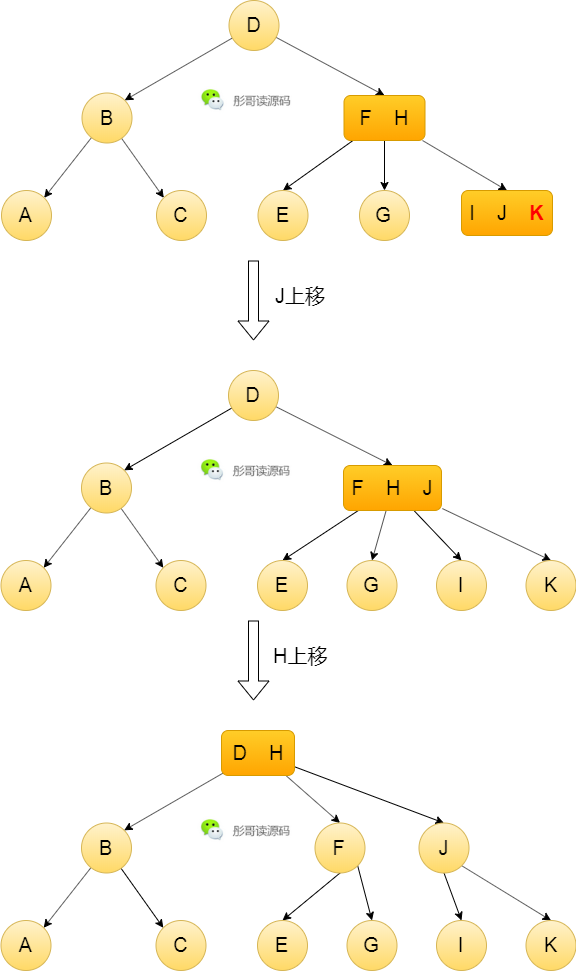
画图辛苦了，关注一波：彤哥读源码。

可以看到，上面自平衡的过程中，出现了一种节点，它具有四个子节点和三个数据元素，这个节点可以称作4节点，如果把4节点当作是可以允许存在的，那么，就出现了另一种树：2-3-4树。

2-3-4树

2-3-4树，它的每个非叶子节点，要么是2节点，要么是3节点，要么是4节点，且可以自平衡，所以称作2-3-4树。

2节点、3节点、4节点的定义在上面已经提及，我们再重申一下：

2节点：包含两个子节点和一个数据元素；

3节点：包含三个子节点和两个数据元素；

4节点：包含四个子节点和三个数据元素；

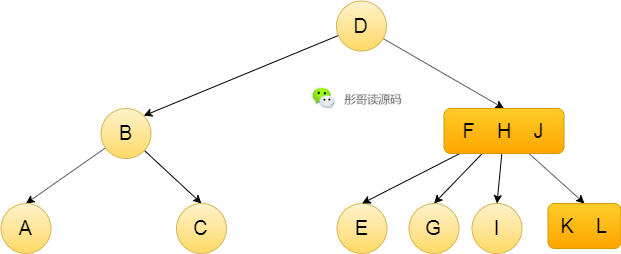
当然，2-3-4树插入元素的过程也很好理解，比如，上面这颗树，插入元素M，找到K L这个节点，插入即可，形成4节点，满足规则，不需要自平衡：

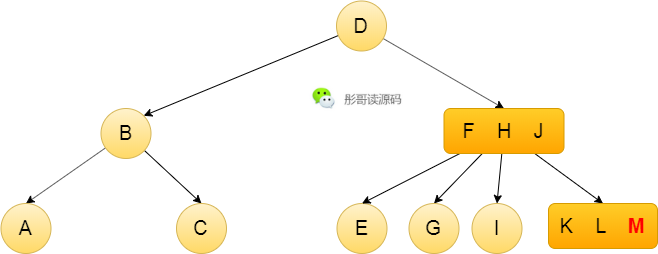
再插入元素N呢？过程与2-3树一样，向上分裂即可，此时，中间节点有两个，取任意一个上移都是可以的，我们这里以左中节点上移为例，大致过程如下：

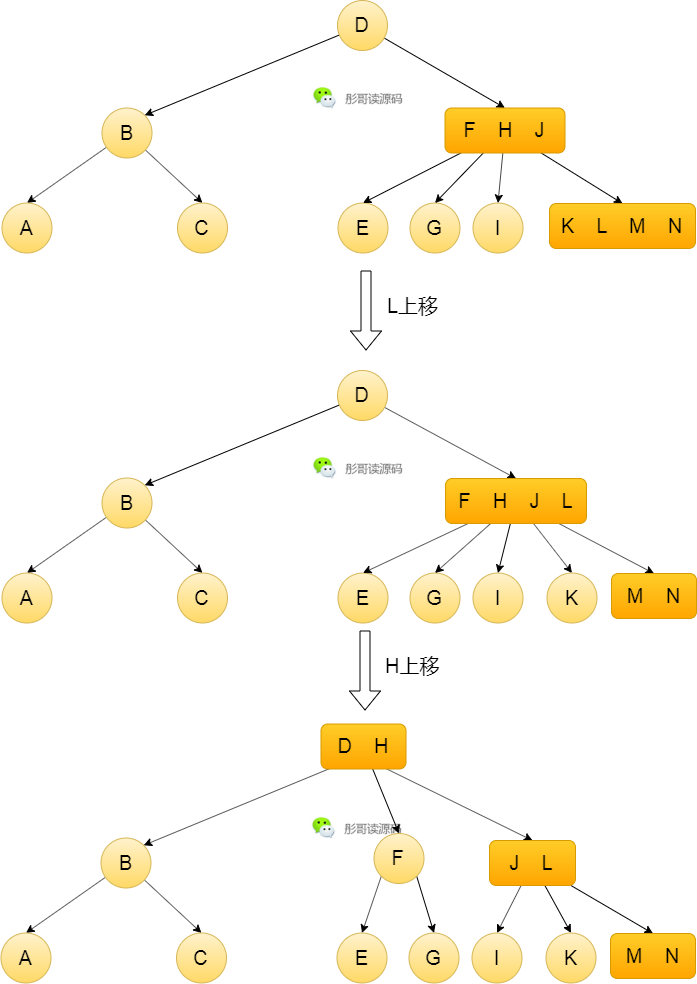
是不是挺简单的，至少比AVL树那种左旋右旋简单得多。

同样地，在2-3-4树自平衡的过程中出现了临时的5节点，所以，如果允许5节点的存在呢？

嗯，2-3-4-5树由此诞生！

同样地，还有2-3-4-5-6树、2-3-4-5-6-7树……子子孙孙，无穷尽也~

所以，有人就把这一类树归纳为一个新的名字：B树。

B树

B树，表示的是一类树，它允许一个节点可以有多于两个子节点，同时，也是自平衡的，叶子节点的高度都是相同的。

所以，为了更好地区分一颗B树到底属于哪一类树，我们给它一个新的属性：度（Degree）。

具有度为3的B树，表示一个节点最多有三个子节点，也就是2-3树的定义。

具有度为4的B树，表示一个节点最多有四个子节点，也就是2-3-4树的定义。

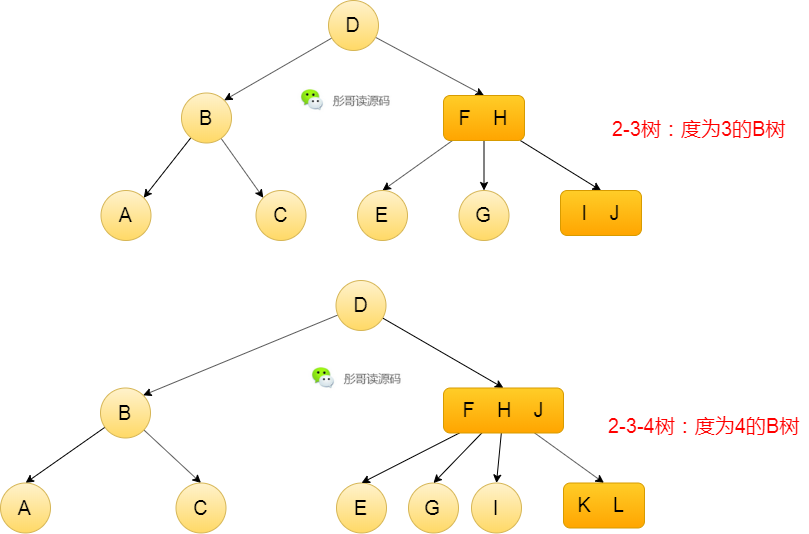
B树，一个节点可以存储多个元素，有利于缓存磁盘数据，整体的时间复杂度趋向于O(log n)，原理也比较简单，所以，经常用于数据库的索引，包括早期的mysql也是使用B树来作为索引的。

但是，B树有个大缺陷，比如，我要按范围查找元素，以上面的2-3-4树为例，查找大于B且小于K的所有元素，该怎么实现呢？

很难，几乎无解，所以，后面又出现替代B树的方案：B+树。

当然了，B+树不是本节的重点，本节的重点是红黑树。

纳尼，红黑树在哪里？写了3000多字了，还没见到红黑树的影子，我尬了~

来了来了，有意思的红黑树来了~~

红黑树

先上一张图，请仔细体会：

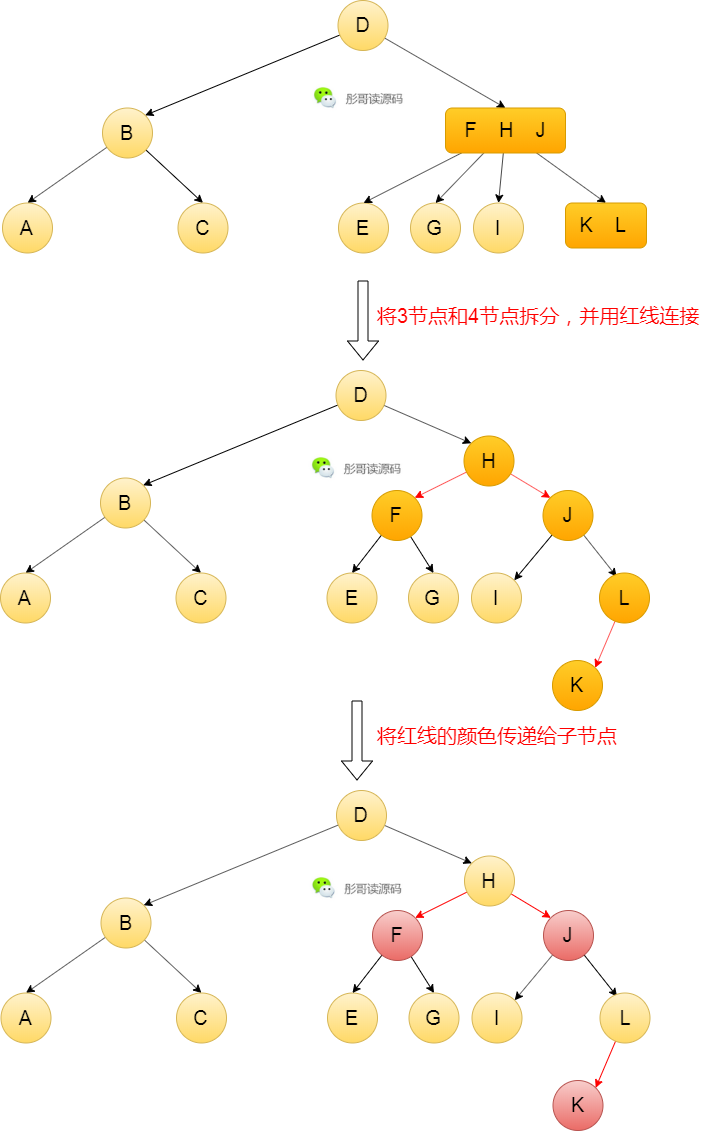
看明白了没有？红黑树是啥？红黑树就是2-3-4树！！！

OK，本节到此结束。

后记

本节，我们一起从二叉树出发，一路经过二叉查找树、平衡树、AVL树、2-3树、2-3-4树、B树，最后终于得出了红黑树的本质，红黑树的本质就是一颗2-3-4树，换了个皮肤而已。

那么，为什么要再造一个红黑树呢？直接用2-3-4树它不香么？

我们下一节解答，同时，下一节，我们将从红黑树的本质出发，彻底理解红黑树插入、删除、查找、左旋、右旋的全过程，再也不用死记硬背了，还不来关注我^^