这是本坑的第四篇,之前已经说了关于 HashSet 、BitMap 、Bloom Filter 布隆过滤器了,本篇主要讲B-树。。
B+树是现在很多索引系统的数据结构,而B-树是B+树的基础,本次先讲B-树。
而在讲B-树之前,又不得不讲二叉搜索树(BST,Binary Search Tree)。二叉搜索树只有一个原则,左子树全部小于根节点,右子树全部大于根节点。
所以在数据 9、17、28、35、39、65 形成二叉树的时候,会有下面这两种截然不同的结构。
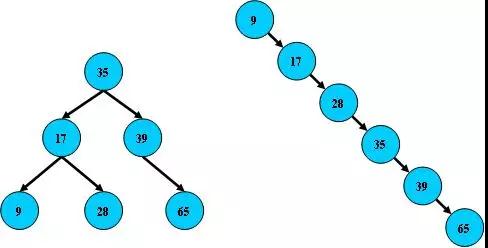
而对于磁盘来说,每一次的搜索,就是一次磁盘索引,树越深,则搜索次数越多,则磁盘IO越多,消耗时间也越多。所以后面又进化出了平衡二叉树这类控制树平衡并以此来控制树的高度的算法。
但即便如此,二叉树在数据量比较大的情况下,深度还是太深。
B-树的出现就是为了解决二叉树又深又窄的结构,进而变成又矮又宽的结构。树越矮代表层次越少,则搜索的次数越少,所以磁盘IO次数越少。B-树继承了BST的优良传统,左子树 < 根节点 <右子树,而且每个树节点都存储了更多的东西。每个节点不仅仅是只存储一个数值,而是存储M-1个数值,以及M个索引,以及额外的索引信息,典型的以空间换时间的数据结构。
一个M阶的B-树的结构定义如下:
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
经典的3阶B-树结构如下:

一个字都看不懂是吗?一个一个讲给你们听哈~
经典的3阶B-树。比如以根节点为例,每个节点都有3个子树。我们可以看到,根节点含有2个(M-1)个数值,这两个数值分割了三个段P1,P2,P3。若值小于17,则继续往下P1所指向的子树搜索。若值大于17而小于35,则往P2所指向子树搜索。若数值大于35,则往P3所指向子树搜索。子树也是相同的操作。
在搜索子树的过程中,若匹配到值完全相等,则搜索结束,并不需要等到叶子节点才算搜索结束(这个记住,在B+树里会不一样)。
因为一个节点和叶子,都存储了M-1个值(并非1个),而且是多路(并非二叉),所以在树的结构上,能比二叉搜索树更加宽,更加矮,这在典型的索引系统中,极大地降低了磁盘的IO次数。因为树很大,但是搜索的次数又比较少,所以大可以将索引存储到磁盘中,而不用全部放在内存里。
有小伙伴就要问了,我特么看了这么久,这跟大数据计数有什么关系呢?
我们之前都是讲,如何将已经出现过的值保存,并索引下来,B-树就是一个很好的数据结构,来进行值的保存。只要不在树中出现过的,插入到树中,并将数值加1,这就可以达到统计的效果了,错误率是0。
好了这个系列也到第四篇了,还请小伙伴们多多给意见才是啊。

 随时随地看视频
随时随地看视频



