本文测试数据:
private static int[] arr = {8, 3, 5, 55, 7, 22, 32, 99};
一、冒泡排序
1.第一版:
循环28次----移动6次
private static void bubbleSort(int arr[]) {
int n = arr.length - 1;
int i, j, t;
for (i = 0; i < n; i++) {//遍历数组
for (j = i + 1; j <= n; j++) {//内层遍历,从i的下一个
if (arr[i] > arr[j]) {// 数组i元素大,则交换
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
}
}
i=0,第一趟
j 从 1 开始,arr[0]>arr[1],交换位置,保证大的数在后面,a[0]=3
j +1 = 2 , 比较a[2]和a[0],arr[0]<arr[2],继续
然后j +1 =3 ,就这样依次将j右移和a[0]比较,这样到最后一个可保证a[0]是最小的

i=1,第二趟
j 从 2 开始,arr[1]>arr[2],交换位置,保证大的数在后面,a[1]=5
j +1 = 2 , 比较a[3]和a[1],arr[1]<arr[3],继续
然后j +1 =3 ,就这样依次将j右移和a[0]比较,这样到最后,可保证a[0],a[1]正确排序

然后同理,经过n趟,小的数移到了前面
2.相邻元素冒泡
循环28次----移动6次
private static void bubbleSort1(int[] arr) {
int n = arr.length - 1;
int i, j, t;
for (i = 0; i < n; i++) {
for (j = n; j > i; j--) {
if (arr[j - 1] > arr[j]) {// 相邻元素两两对比,如果前者大,交换位置
t = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = t;
}
}
}
}
i=0,第一趟
相邻两个元素比较,小的往左走
i=1,第二趟
相邻两个元素比较,小的往左走
3.优化版冒泡
循环22次----移动6次
// 平均T复杂度 稳定 最好 最坏 辅助空间
//冒泡排序: O(n^2) YES O(n) O(n^2) O(1)
private static void bubbleSort2(int[] arr) {
int n = arr.length - 1;
int i, j, t;
boolean flag = true;
for (i = 0; i < n && flag; i++) {
//如果退出j循环时flag=false,说明本循环没有元素交换,说明已排序完成
flag = false;
for (j = n; j > i; j--) {
if (arr[j - 1] > arr[j]) {// 相邻元素两两对比,如果前者大,交换位置
t = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = t;
flag = true;
}
}
}
}
二、选择排序
循环28次----移动6次
// 平均T复杂度 稳定 最好 最坏 辅助空间
//选择排序: O(n^2) YES O(n^2) O(n^2) O(1)
public static void selectSort(int[] arr) {
int n = arr.length - 1;
int i, j, t, min;
for (i = 0; i < n; i++) {
min = i;
for (j = i + 1; j <= n; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
if (min != i) {//如果min和i相同,没必要交换
t = arr[i];//交换
arr[i] = arr[min];
arr[min] = t;
}
}
}
在j循环中记录发现的最小值所在索引,如果min不是i,交换元素
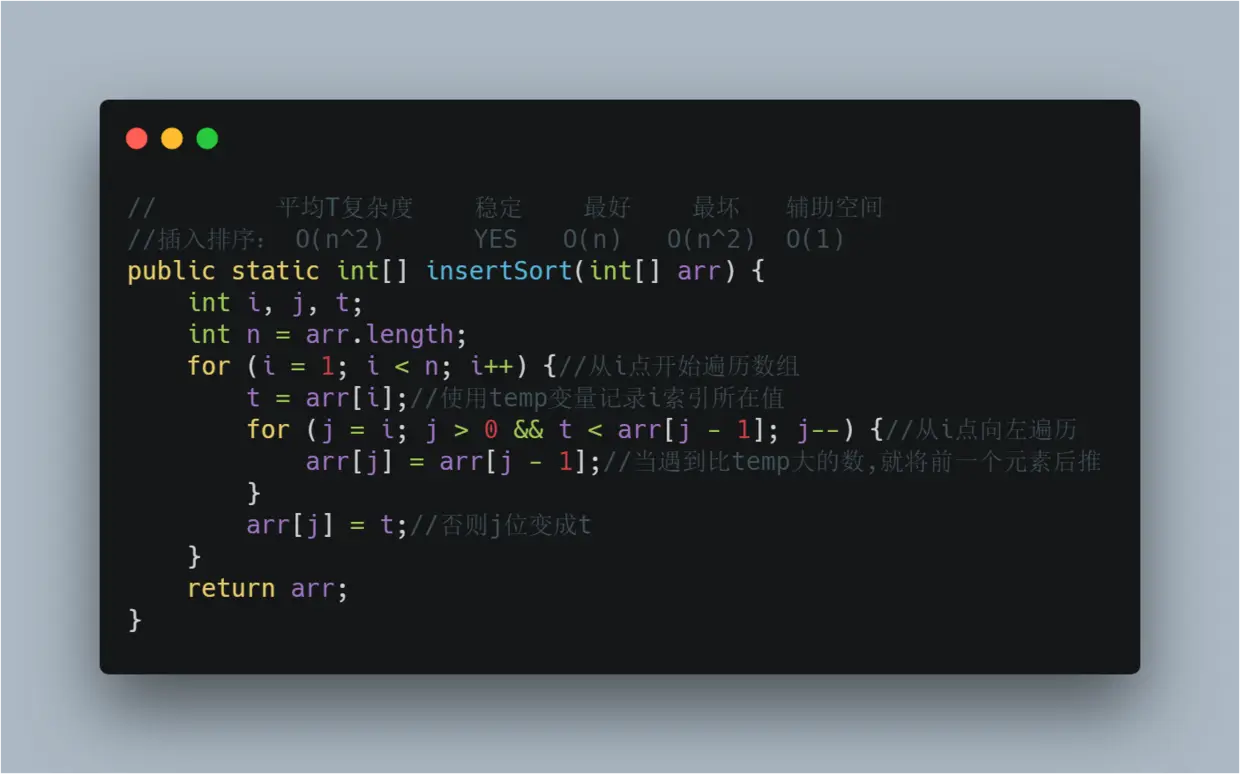
三、插入排序
1.具体算法
// 平均T复杂度 稳定 最好 最坏 辅助空间
//插入排序: O(n^2) YES O(n) O(n^2) O(1)
public static int[] insertSort(int[] arr) {
int i, j, t;
int n = arr.length;
for (i = 1; i < n; i++) {//从i点开始遍历数组
t = arr[i];//使用temp变量记录i索引所在值
for (j = i; j > 0 && t < arr[j - 1]; j--) {//从i点向左遍历
arr[j] = arr[j - 1];//当遇到比temp大的数,就将前一个元素后推
}
arr[j] = t;//否则j位变成t
}
return arr;
}
2.分析
第一轮排序
i,j从索引1开始, t=3 ,
t与j前一个元素比较, 3<8 , j处值变成较大值 8 , j 向左指一位
跳出j的for循环后,将j索引置为刚才保存的临时变量t=3,此时前两个元素排序完成。
第二轮排序
i索引右移一格到2,t= 5 ,j 从索引2开始
t与j前一个元素比较, 5 < 8 , j处值变成较大值 8 , j 向左指一位
t与j前一个元素比较, 5 > 3 , 跳出j循环
将j索引置为刚才保存的临时变量t=3,此时前3个元素排序完成。
第三轮排序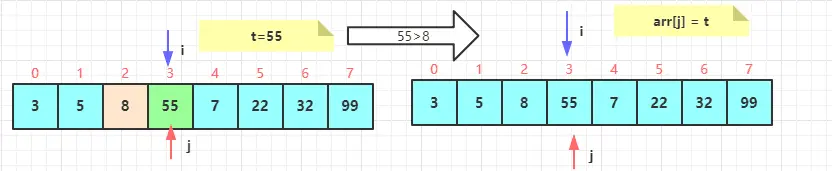
i索引右移一格到3,t= 55 ,j 从索引3开始
t与j前一个元素比较, 55 > 8 , 跳出j循环
将j索引置为刚才保存的临时变量t=55,此时前4个元素排序完成。
第四轮排序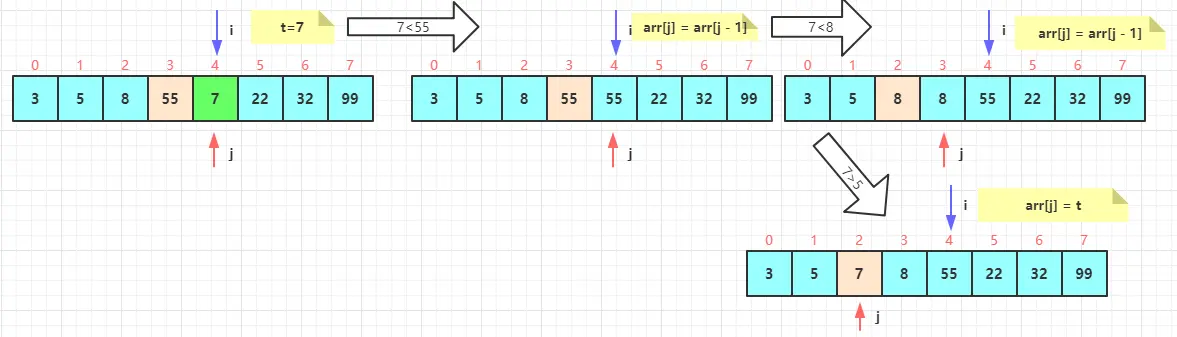
i索引右移一格到4,t= 7 ,j 从索引4开始
t与j前一个元素比较, 7 <55 , j处值变成较大值 55 , j 向左指一位 为3
t与j前一个元素比较, 7 < 8 , j处值变成较大值 8 , j 向左指一位 为2
t与j前一个元素比较, 7 > 5 , 跳出j循环
将j索引置为刚才保存的临时变量t=7,此时前5个元素排序完成。
插入排序第n轮排序后将前n+1个元素是顺序的
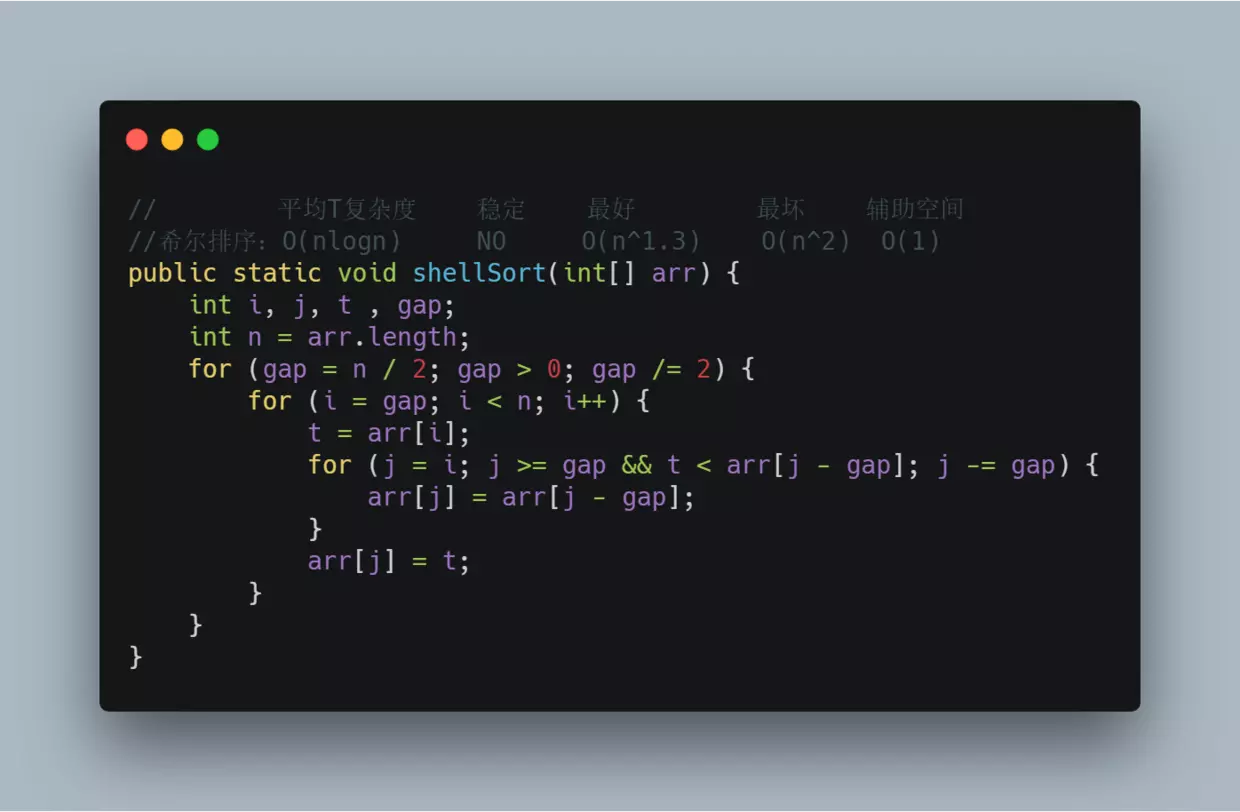
四、希尔排序
试了一下开篇中100W的随机整数,果然不愧为N*logN的算法, 0.365秒
// 平均T复杂度 稳定 最好 最坏 辅助空间
//希尔排序:O(nlogn) NO O(n^1.3) O(n^2) O(1)
public static void shellSort(int[] arr) {
int i, j, t , gap;
int n = arr.length;
for (gap = n / 2; gap > 0; gap /= 2) {
for (i = gap; i < n; i++) {
t = arr[i];
for (j = i; j >= gap && t < arr[j - gap]; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = t;
}
}
}

希尔排序先将数据归整,最后gap=1时,相当于归整后的插入排序
开始gap取4,图中相同颜色进行比较,用的是插入排序交换的套路
然后gap减半=2,图中相同颜色进行比较,用的是插入排序交换的套路
然后gap减半=1,图中相同颜色进行比较,用的是插入排序交换的套路
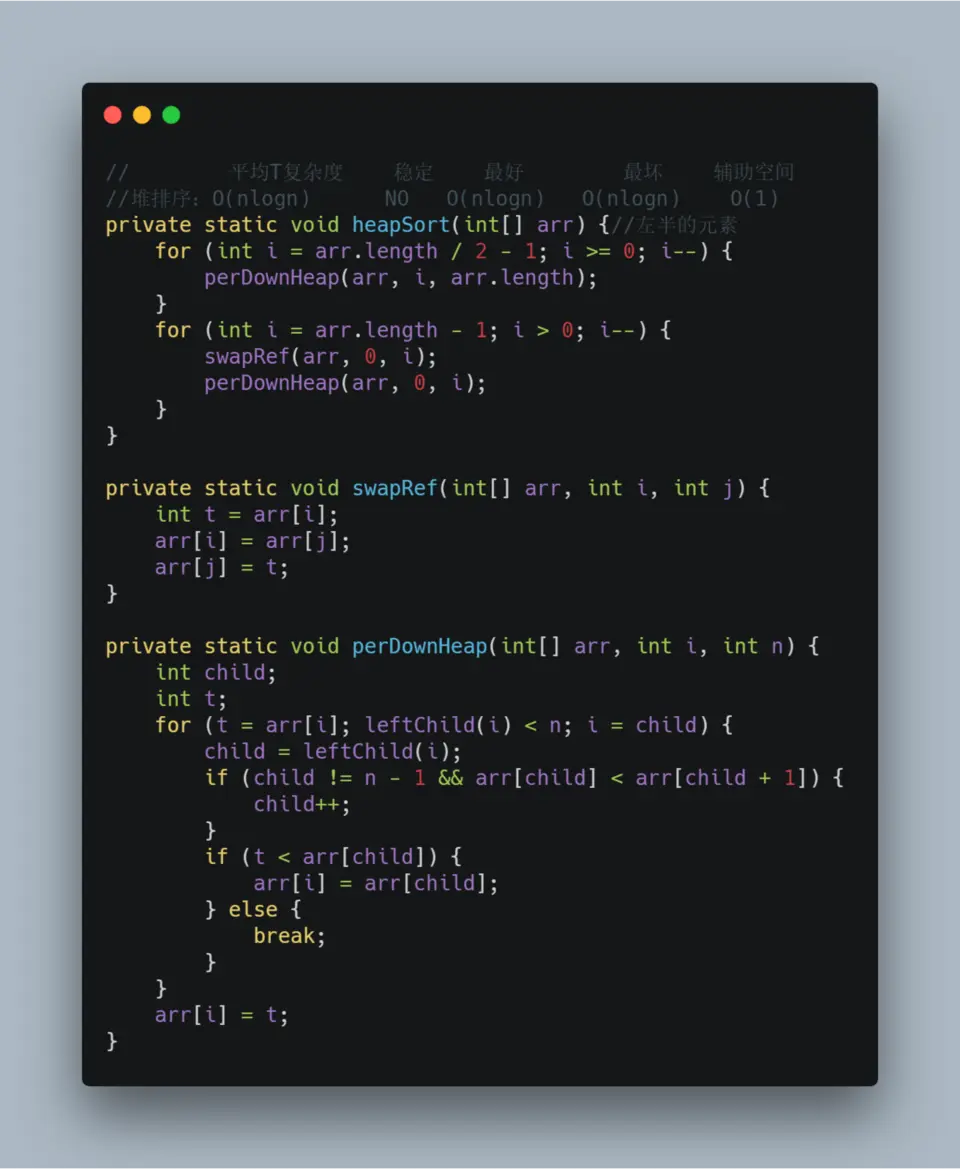
五、堆排序
1.具体算法
试了一下开篇中100W的随机整数,果然不愧为N*logN的算法, 0.286秒
// 平均T复杂度 稳定 最好 最坏 辅助空间
//堆排序:O(nlogn) NO O(nlogn) O(nlogn) O(1)
private static void heapSort(int[] arr) {//左半的元素
for (int i = arr.length / 2 - 1; i >= 0; i--) {
perDownHeap(arr, i, arr.length);//形成堆
}
for (int i = arr.length - 1; i > 0; i--) {
swapRef(arr, 0, i);//交换首
perDownHeap(arr, 0, i);//维持堆形状
}
}
private static void swapRef(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
private static void perDownHeap(int[] arr, int i, int n) {
int child;
int t;
for (t = arr[i]; leftChild(i) < n; i = child) {
child = leftChild(i);
if (child != n - 1 && arr[child] < arr[child + 1]) {
child++;
}
if (t < arr[child]) {
arr[i] = arr[child];
} else {
break;
}
}
arr[i] = t;
}
2.分析

第一次执行的是:perDownHeap(arr, 3, arr.length);
private static void perDownHeap(int[] arr, int i, int n) {
int child;//0
int t;//55
for (t = arr[i]; leftChild(i) < n; i = child) {
child = leftChild(i);//7 arr[child]=99 即 55的左子是99
if (child != n - 1 && arr[child] < arr[child + 1]) {//此时条件不满足
child++;
}
if (t < arr[child]) {//走这里 55<99 条件满足
arr[i] = arr[child];//arr[3]=99
} else {
break;
}
}
arr[i] = t;//跳出循环, i = child ,arr[7]=t=55
}
第二次执行的是:perDownHeap(arr, 2, arr.length);
private static void perDownHeap(int[] arr, int i, int n) {
int child;//0
int t;//5
for (t = arr[i]; leftChild(i) < n; i = child) {
child = leftChild(i);//5 arr[child]=22 即 5的左子是22 ,右子是arr[child + 1]=32
if (child != n - 1 && arr[child] < arr[child + 1]) {//此时条件满足
child++;//child = 6
}
if (t < arr[child]) {//走这里 5<32 条件满足
arr[i] = arr[child];//arr[2]=32
} else {
break;
}
}
arr[i] = t;//跳出循环, i = child ,arr[6]=t=5
}
>其他同上...绘图如下

接下来通过交换根节点和i,再对堆进行沉浮,形成小顶堆
for (int i = arr.length - 1; i > 0; i--) {
swapRef(arr, 0, i);
perDownHeap(arr, 0, i);
}




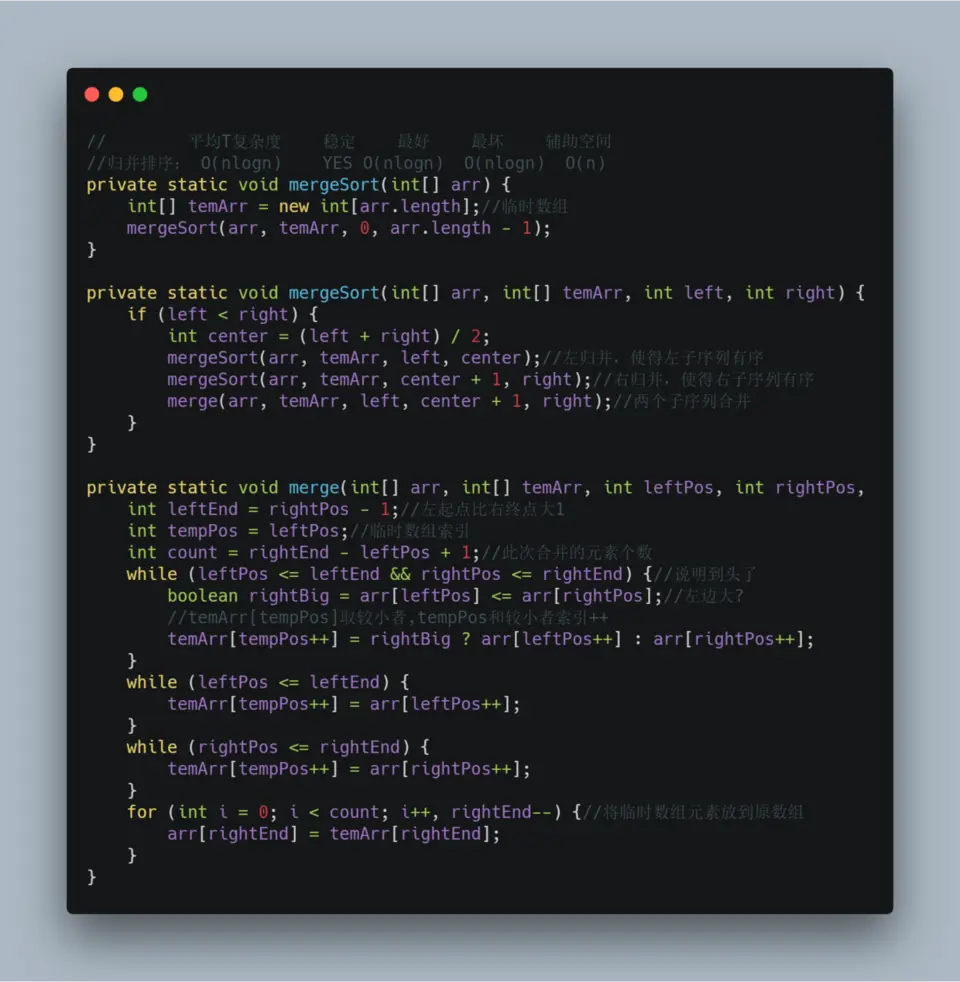
六、归并排序
1.具体算法
private static void mergeSort(int[] arr) {
int[] temArr = new int[arr.length];//临时数组
mergeSort(arr, temArr, 0, arr.length - 1);
}
private static void mergeSort(int[] arr, int[] temArr, int left, int right) {
if (left < right) {
int center = (left + right) / 2;
mergeSort(arr, temArr, left, center);//左归并,使得左子序列有序
mergeSort(arr, temArr, center + 1, right);//右归并,使得右子序列有序
merge(arr, temArr, left, center + 1, right);//两个子序列合并
}
}
private static void merge(int[] arr, int[] temArr, int leftPos, int rightPos,
int leftEnd = rightPos - 1;//左起点比右终点大1
int tempPos = leftPos;//临时数组索引
int count = rightEnd - leftPos + 1;//此次合并的元素个数
while (leftPos <= leftEnd && rightPos <= rightEnd) {//说明到头了
boolean rightBig = arr[leftPos] <= arr[rightPos];//左边大?
//temArr[tempPos]取较小者,tempPos和较小者索引++
temArr[tempPos++] = rightBig ? arr[leftPos++] : arr[rightPos++];
}
while (leftPos <= leftEnd) {
temArr[tempPos++] = arr[leftPos++];
}
while (rightPos <= rightEnd) {
temArr[tempPos++] = arr[rightPos++];
}
for (int i = 0; i < count; i++, rightEnd--) {//将临时数组元素放到原数组
arr[rightEnd] = temArr[rightEnd];
}
}
2.分析

|--- 第一次merge: merge(arr, temArr, 0, 1, 1)
leftPos:0
leftEnd:0
arr[leftPos]:8
rightPos:1
rightEnd:1
arr[rightPos]:3
temArr[0] = arr[leftPos]和arr[rightPos]的较小者:arr[rightPos]=3
temArr[1] = arr[leftPos++] = 8
将临时数组元素放到原数组
|--- 第二次merge: merge(arr, temArr, 2, 3, 3)
leftPos:2
leftEnd: 2
arr[leftPos]:5
rightPos:3
rightEnd:3
arr[rightPos]:55
temArr[0] = arr[leftPos]和arr[rightPos]的较小者 arr[leftPos]=5
temArr[1] = arr[rightPos++] = 55
将临时数组元素放到原数组
|--- 第三次merge: merge(arr, temArr, 0, 2, 3)
leftPos:0
leftEnd: 1
arr[leftPos]:3
rightPos:2
rightEnd:3
arr[rightPos]:5
见下图...
第三次 merge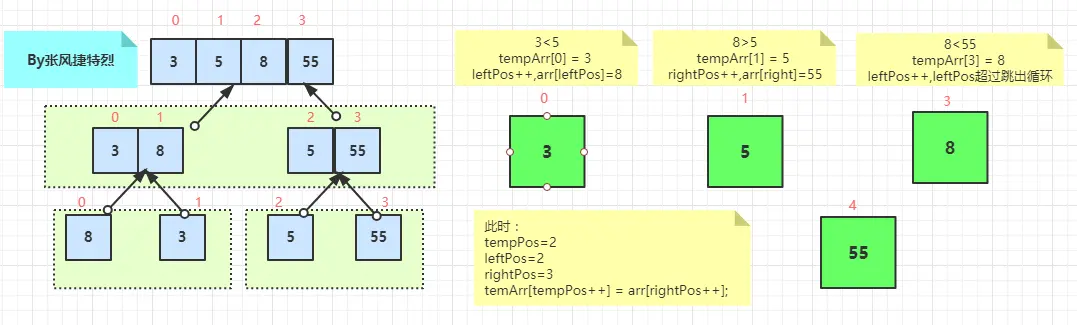
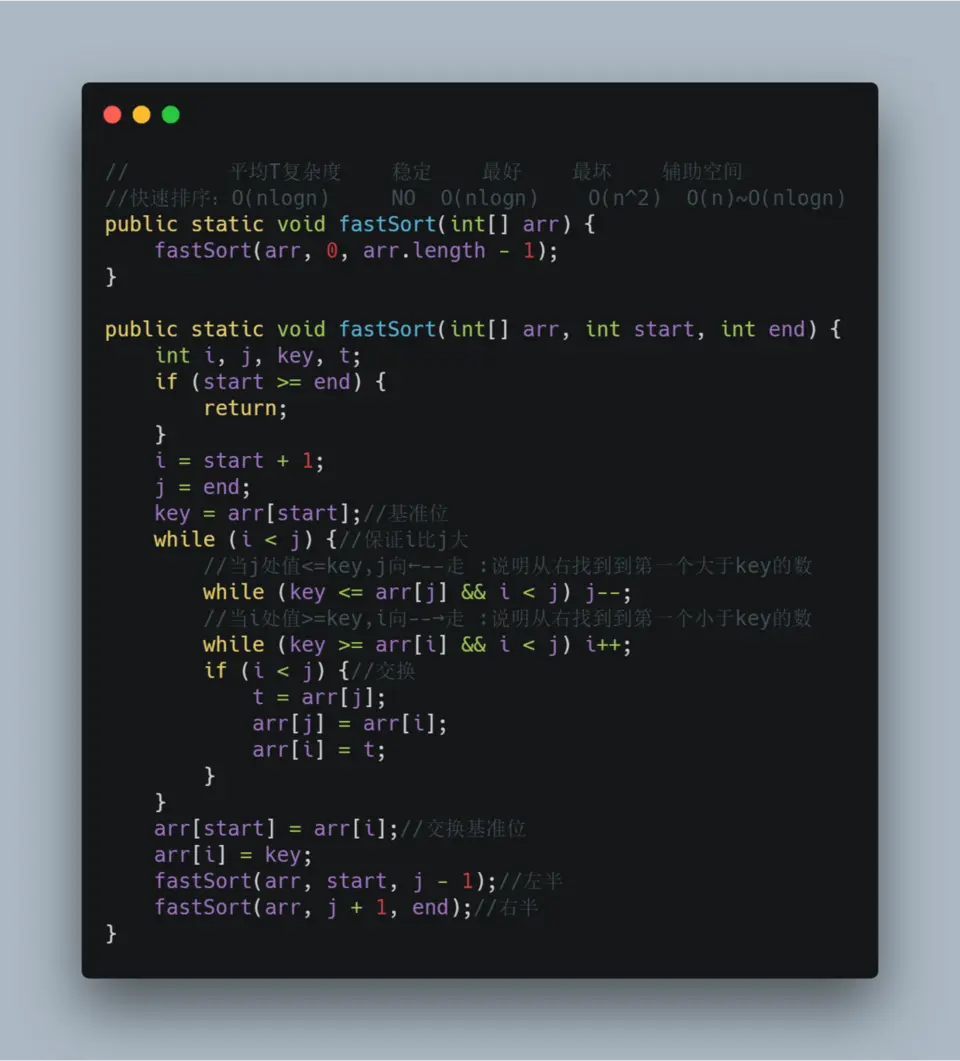
七、快速排序
1.具体算法
// 平均T复杂度 稳定 最好 最坏 辅助空间
//快速排序:O(nlogn) NO O(nlogn) O(n^2) O(n)~O(nlogn)
public static void fastSort(int[] arr) {
fastSort(arr, 0, arr.length - 1);
}
public static void fastSort(int[] arr, int start, int end) {
int i, j, key, t;
if (start >= end) {
return;
}
i = start + 1;
j = end;
key = arr[start];//基准位
while (i < j) {//保证i比j大
//当j处值<=key,j向←--走 :说明从右找到到第一个大于key的数
while (key <= arr[j] && i < j) j--;
//当i处值>=key,i向--→走 :说明从右找到到第一个小于key的数
while (key >= arr[i] && i < j) i++;
if (i < j) {//交换
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
arr[start] = arr[i];//交换基准位
arr[i] = key;
fastSort(arr, start, j - 1);//左半
fastSort(arr, j + 1, end);//右半
}
分析:
Q1:第一趟sort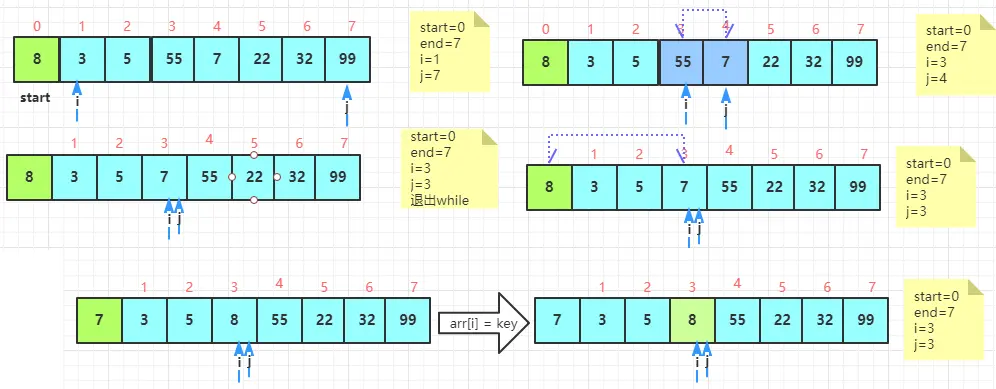
此时调用了:
sort(arr, 0, 2);//对左半元素快速排序
Q1.1:Q1左半sort
Q1.1.1:Q1.1左半sort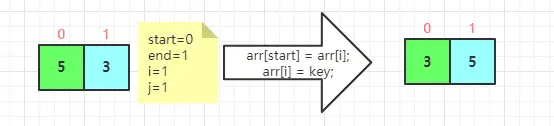
Q1.1.2:Q1.1右半sort:一个元素不用排序,直接returnQ1.2:Q1右半sort:套路一样,就不分析了
小结:没有最好的排序,只有最适合的排序。

数据量较小时:冒泡排序,选择排序,插入排序就可以了
数据量非常大时:最好用O(nlogn)复杂度的算法
如果数据基本是有序的:插入排序
数据随机性很大:快速排序
需要要求稳定性且O(nlogn):归并排序是唯一的选择,代价是需要多消耗一倍空间
如果不想出现最坏情况,也就是想一切在预期之内:堆排序是你不二的选择
排序的稳定性:大小相同的元素在排序前后顺序有没有可能改变
设:Ki=Kj (1<=i<=n,1<=j<=n,i!=j)且在排序前ri先于rj(即i<j)
|--- 排序后ri仍先于rj,则排序方法稳定,反之,不稳定
下面用七张图记录一下:

ok,就先这样,以后有想到什么再补充













 随时随地看视频
随时随地看视频




