此题来源:算法竞赛入门经典(第2版) P21
/**
* 输入n, 计算 S = 1! + 2! + ... n! 的末六位(不含前导0)。
* n < 10^6
* n! 表示阶乘, 是前n个正整数之积
* 样例输入:10
* 样例输出:37913
**/
乍一看,这道题目并不难,无非是一个循环求和,里面套一个求阶乘。
给出最基础版本的示例代码如下:
f1 基础版本
/** with bug
* @param int $n
* @return int
*/
function f1 (int $n):int
{
for($fnum = 1,$sum = 0;$fnum<=$n;$fnum++){
for($multi_num = 1,$fa_res = 1;$multi_num<=$fnum;$multi_num++){
$fa_res *= $multi_num;// 计算 fnum!
}
$sum += $fa_res; // 求和 重复到n
}
return $sum%1000000;
}
这个代码看似并没有什么问题,逻辑上也没看到什么异常。那么我们来运行一下试试!
为了方便进行后续的优化对比,我们再外部的主程序里调用这个函数,测试一下当n从 10到10000的运行结果,每次n的规模扩大两倍 ,并且输出它的运行时间。调用的函数如下:
//time
for($num = 10;$num<10000;$num*=2) {
echo PHP_EOL."num: $num:".PHP_EOL;
$start_time = microtime(true);
echo f1($num);
$end_time = microtime(true);
$time = 1000 * ($end_time - $start_time);
echo PHP_EOL . "time:$time ms" . PHP_EOL;
}
运行的结果却发现,n=40 的时候的出来的结果居然变成0了!!
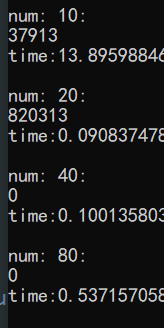
f1的debug过程
我们把内部 f1 的函数里面,输出求和结果$sum,把再细调一下外部的调用程序,把for循环的 num 步长调成 $num++ ,从10到40运行一下试试。
//time
for($num = 10;$num<40;$num++) { .... }
运行的结果如下:
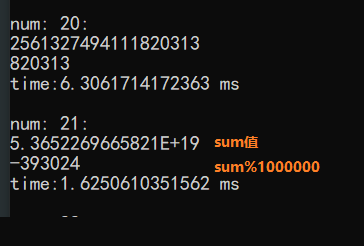
当num=21的时候, 居然输出了一个负数。原因是什么呢? 可以看到sum出来的值已经不再是直接一个整数输出了,而是用了 E形式 的浮点数表示法。这是因为sum值已经很大,超出了int表示范围,php是弱类型语言,因此将其自动转为了其他的数据类型。
为了更好的看清楚具体的数据变化,我们可以增加一些内容来看清楚他的变化过程
function f1 (int $n):int
{
for($fnum = 1,$sum = 0;$fnum<=$n;$fnum++){
for($multi_num = 1,$fa_res = 1;$multi_num<=$fnum;$multi_num++){
$fa_res *= $multi_num;// 计算 fnum!
}
$sum += $fa_res; // 求和 重复到n
}
//输出sum值以及类型
echo 'sum-type:'.gettype($sum).PHP_EOL;
echo 'sum:'.$sum.PHP_EOL;
//输出data值以及类型
$data = $sum%1000000;
echo 'data-type:'.gettype($data).PHP_EOL;
echo 'data:'.$data.PHP_EOL;
return $data;
}
执行结果如下:
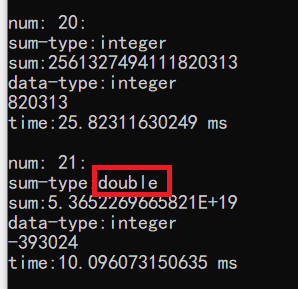
当num=21的时候,求出来的sum值已经很大了,于是执行这一条语句$sum%1000000 的时候,实际上是一个 double值 % int值,在这个取余%的运算过程中,double 被强转成存储更小的 int 型,导致溢出数据的异常运算,得到一个错误的 int 结果。
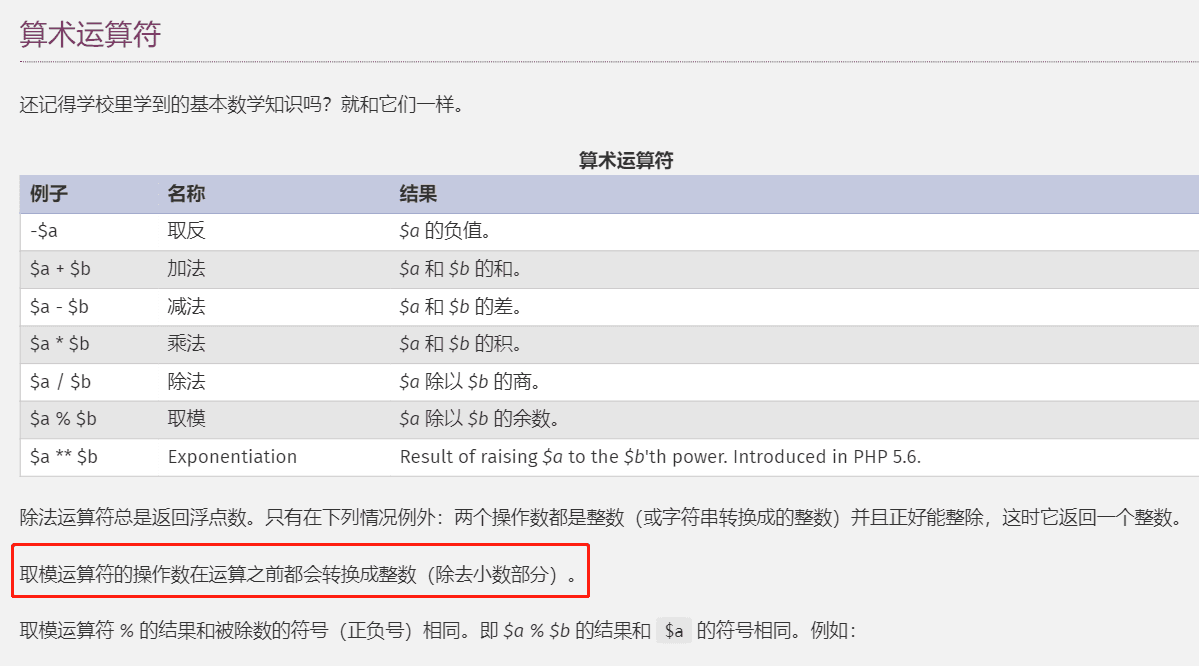
那么我们应该如何解决这个bug呢 ?
显然,问题出在 int值 % int值 这个运算流程上。简单来说无非两种解决思路。
- 修改流程,使其运算的值不溢出,能以 int 值正常运算
- 修改
%运算,用别的方法获取末六位的值(比如字符处理)
不溢出的修改 — f2()
首先试下第一种解决思路,让数字不要那么大。
我们的目的是计算 S = 1! + 2! + … n! 的末六位,那么其实我们只关心末六位的变化。而这末六位的变化,其实都是一个个阶乘结果的和,那也就是说,我们只关心阶乘结果的末六位。
因此,在每次求出 n! 的结果的时候,就可以进行一次取余运算,获取其末六位,再做相加的操作。
/** 提前取mod
* @param int $n
* @return int
*/
define('MOD',1000000);
function f2 (int $n):int
{
for($fnum = 1,$sum = 0;$fnum<=$n;$fnum++) {
for ($multi_num = 1, $fa_res = 1; $multi_num <= $fnum; $multi_num++) {
$fa_res = ($fa_res * $multi_num)%MOD ;// 计算 fnum!
}
$sum = ($sum + $fa_res) % MOD; // 求和 重复到n 这里提前取mod
// echo $fnum . '! mod = ' . $fa_res . PHP_EOL;
// echo 'sum-mod:'.$sum . PHP_EOL;
}
return $sum;
}
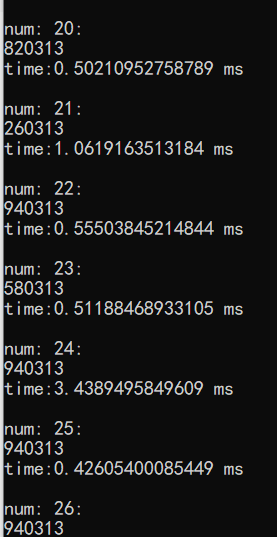
运行结果如下:
第二种解决思路,修改 % 运算,用别的方法来实现,这种方法也是可以的。但是要做到效率不输于 % 才是一种好的方法。此处先暂放,后续想到好方法再继续补上~
我们还发现,这个运行结果里,当 num 为 24,25,26的时候,输出的结果是一样的, 都是940313 ,那么会不会存在着什么规律呢?
我们来用计算器算一下 25!, 结果发现是下面这个数

也就是说,计算S的过程中,当计算到 25! 以及之后更大的数,末六位都是0的,不会有更多的项用于求和,所以之后的num都是可以不用算的!直接输出结果就可以。因此,我们可以改进成如下的代码。
大数改进版本 — f3()
/** 改进大数情况
* @param int $n
* @return int
*/
define('MOD',1000000);
function f3 (int $n):int
{
if($n>24) $n = 24;//发现的规律 大数不处理
for($fnum = 1,$sum = 0;$fnum<=$n;$fnum++) {
for ($multi_num = 1, $fa_res = 1; $multi_num <= $fnum; $multi_num++) {
$fa_res = ($fa_res * $multi_num) % MOD;// 计算 fnum!
}
$sum = ($sum + $fa_res) % MOD; // 求和 重复到n
}
return $sum;
}

再来继续审题,我们要计算 S = 1! + 2! + … n! 的末六位,无非是三个操作,求阶乘,求和,求末六位。求和和末六位已经做了相关的优化了,那么求阶乘是不是也能做一些优化呢?
我们目前的求阶乘计算方法是,用一个for循环,每次从1开始乘,实现 n! = 1*2*3*... *n 的计算,但是这里面是有重复的部分的。
既然第一次已经计算出了 1! 的值,那么第二次算 2! 的时候,其实是可以把前面的运算结果用上的。我们在再把数字放大一些,这个性能优势就会非常明显了。
假设我已经求15!,前面已经算出了 1! 的值,后面下一个相加的项,就是这个结果值*2 即可,得到2!。 同理3! , 就是 2! * 3。这样逐步运算下去,就把之前的for循环累乘的过程,变成了每次只进行一次乘法运算即可,因此就可以更快完成运算。
当然,时间性能提升与之对应的就是空间占用的开销,需要用一个额外的数组来保存中间的临时结果。当然,后面也会有除了数组保存之外的方法。
用数组保存中间结果避免循环 — f4()
具体代码如下:
/** 改进大数 保存中途结果减少循环
* @param int $n
* @return int
*/
function f4 (int $n):int
{
if($n>25) $n =25;//发现的规律
$fa_res = [];
$fa_res[] = 1;
for($fnum = 1,$sum = 0;$fnum<=$n;$fnum++) {
if (empty($fa_res[$fnum])){
$fa_res[$fnum] = ($fnum * $fa_res[$fnum-1])%MOD; // 利用上一次的保存结果
}
$sum = ($sum + $fa_res[$fnum]) % MOD; // 求和 重复到n
}
return $sum;
}

再来回头看我们的f4() 函数,我们用了一个数组来保存求和结果,但是实际上,我们每次只是用了上一次的结果,我只需要1个内容而已,因此这里完全可以用1个变量来保存,之前已经用过的临时值就可以扔掉了。
另外也再看看提前取mod操作,做这个操作,是为了避免值太大超出int的范围,那么其实只需要在它快要超出int值,快要爆掉的时候取一下就可以了。不需要每次都去做这个运算。
我们之前测试的时候已经知道,当n=20还是能正常运算的,当n=21才会出现double的情况,因此我们只需要对这几个大数的情况处理就可以了。如果到达了大数临界的情况,并且sum是超过6位了,才有必要进行取余获取其末六位
因此我们还可以在进一步优化,得到下面这个版本。
用变量保存中间结果 + 取mod优化 — f5()
/** 用变量保存中间结果 + 取mod优化
* @param int $n
* @return int
*/
function f5(int $n): int
{
if ($n > 24) $n = 24;//发现的规律
$fa_res = 1;
for ($fnum = 1, $sum = 0; $fnum <= $n; $fnum++) {
if ($n > 20 && $sum > 999999) { //如果大数临界 并且sum是超过6位了 才有必要进行取余
$fa_res = ($fnum * $fa_res)%MOD;
$sum = ($sum + $fa_res)%MOD;
} else {
$fa_res = $fnum * $fa_res; // 利用上一次的保存结果
$sum = $sum + $fa_res; // 求和 重复到n
}
}
return $sum > 999999 ? $sum%MOD : $sum;
}

不过呢,其实做到这个地步,已经开始有一些投机取巧的味道在里面了,实际上这里的运算求末六位运算结果,只可能有24种情况,也就是对应 n=1 到 n=24。如果还要进一步追求性能,这种情况数目比较小的东西,完全可以写死。
也就是说,先做一个简单的程序,把这24种情况全部求出来,然后把结果写死,实际求值就直接读取数据即可。
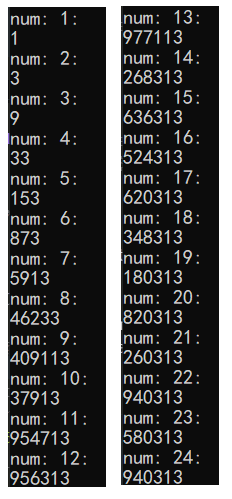
运行结果也就无非是上面的情况,于是直接定义一个常量保存起来。(PHP7支持数组常量,如果是PHP5可以把数组用json_encode() 转成字符串存起来)
/** 直接读取结果
* @param int $n
* @return int
*/
define('RES', [1, 3, 9, 33, 153, 873, 5913, 46299, 409113, 37913, 954713, 956313, 977113,
268313, 636313, 524313, 620313, 348313, 180313, 820313, 260313, 940313, 580313, 940313]);
function f6(int $n): int
{
if ($n > 24) $n = 24;
return RES[$n-1];
}
综合测试
那么我们直接取 num = 1000000 进行一次测试,看下不同的版本性能速度会差多少。PHP默认是单线程的,因此用i5-8250U 运行至多只会吃满1个核,占25%的CPU。
然后结果是f2 运行时间太长了…
我们再来换个测试,取 num 从1到10000,看下不同的版本性能速度会差多少。
//测试调用
for ($num = 1; $num <= 10000; $num *= 10) {
echo PHP_EOL . "num: $num:" . PHP_EOL;
for ($fname = 2; $fname <= 6; $fname++) {
$func_str = 'f' . $fname;
$start_time = microtime(true);
$func_str($num);
$end_time = microtime(true);
$time = 1000 * ($end_time - $start_time);
echo "$func_str -- time:$time ms" . PHP_EOL;
}
}
f2 函数是提前取mod,f3 函数是改进了大数情况,f4 函数是改进大数+数组保存中途结果,f5 函数是改进大数+变量保存中途结果+改进取MOD ,f6 函数是直接取结果。
分别得到执行时间如下。
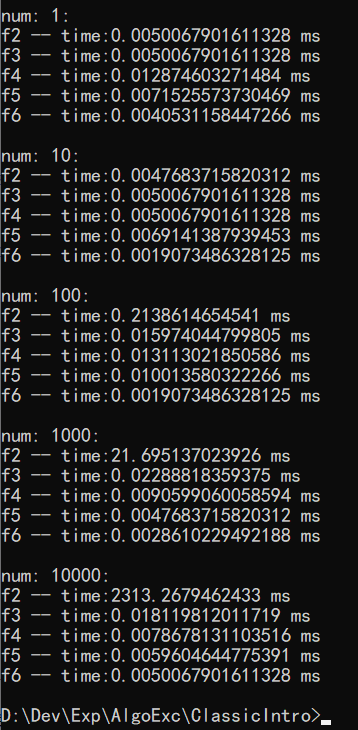
当n特别小的时候,比如 n=1 ,这时候发现其实优化过的算法反而更慢。原因是因为本来的运算量就非常小,我们去操作数组,以及操作数据,执行判断,这些操作所需的时间,是比普通运算慢得多的。特别是CPU要去调用内存数据的时候,这里的IO开销是非常大的(查缓存,调内存,更新缓存)。
因此在考虑性能的时候,要尽量减少不必要的递归,以及大量的值传递。每次开辟对应的内存空间,寻址调用,回收内存空间都是一笔性能开销。当然,php自己本身会去做这些事情,php7也有了较好的性能提升,但在程序设计的角度,这些性能优化都应该是编程的潜意识。

另外,编程语言以及环境平台本身也是一个瓶颈之处。上面同样的测试代码,同样的系统配置,在linux下运行结果如下:
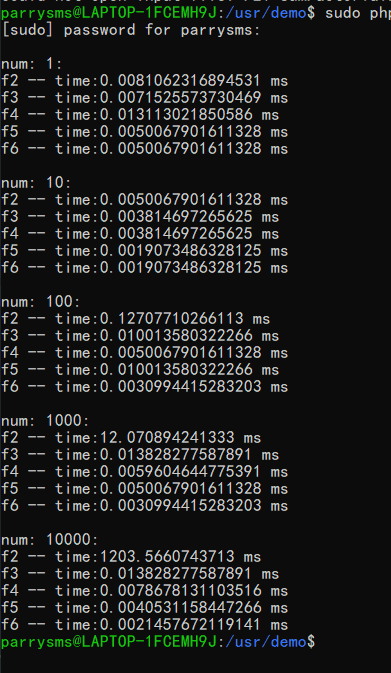
可以看到,ubuntu 里的 php 比 win10是要更快接近1.5到2倍的,而 php 本身呢,底层都是C语言实现的,所以要是用C语言写一下我们 f5() 函数的话。
C语言版本的f5
代码如下:
#include <stdio.h>
#include <sys/time.h>
#define MOD 1000000
int f5(int);
int main() {
struct timeval tv1;
struct timeval tv2;
int t=10000;
gettimeofday(&tv1,NULL);
while(t--) {
f5(10000);
}
gettimeofday(&tv2,NULL);
printf("1 start, now, sec=%ld m_sec=%d \n", tv1.tv_sec, tv1.tv_usec);
printf("2 start, now, sec=%ld m_sec=%d \n", tv2.tv_sec, tv2.tv_usec);
return 0;
}
int f5(int n) {
int fa_res,fnum,sum;
if (n > 24) n = 24;//发现的规律
fa_res = 1;
for (fnum = 1, sum = 0; fnum <= n; fnum++) {
if (n > 20 && sum > 999999) { //如果大数临界 并且sum是超过6位了 才有必要进行取余
fa_res = (fnum * fa_res)%MOD;
sum = (sum + fa_res)%MOD;
} else {
fa_res = fnum * fa_res; // 利用上一次的保存结果
sum = sum + fa_res; // 求和 重复到n
}
}
return sum > 999999 ? sum%MOD : sum;
}
因为在C语言下,这个函数运行的实在是太快,我们使用一个循环,来统计执行10000次的时间,用来估算每次执行的时间。
在 win10平台 和 ubuntu平台 下,运行结果如下:
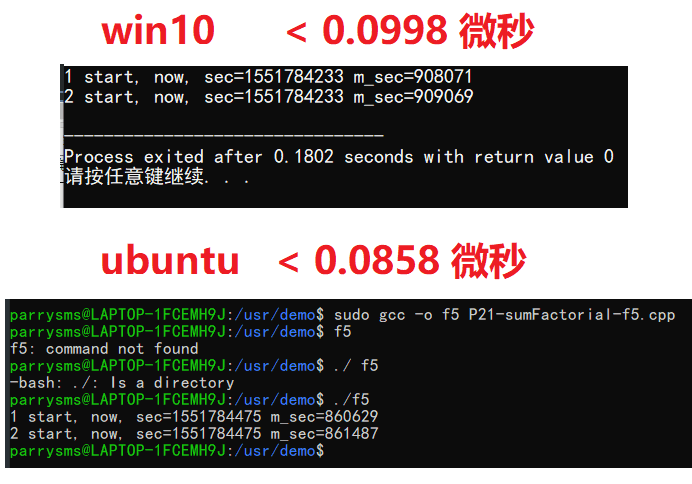
1微秒 = 0.001毫秒,换个C语言直接完爆PHP。
最后我们拿个表格汇总一下
num = 10000 的测试结果表
| 函数时间 /ms | 语言 | win10 | ubuntu | 性能提升 |
|---|---|---|---|---|
| f1 | PHP | 2313.2679 | 1203.5661 | 1 |
| f2 | PHP | 0.0181 | 0.0138 | 10万倍 |
| f3 | PHP | 0.0079 | 0.0079 | 约2倍 |
| f4 | PHP | 0.0060 | 0.0041 | 约1.5到2倍 |
| f5 | PHP | 0.0050 | 0.0021 | 约1.5到2倍 |
| f5 | C | 0.0000998 | 0.0000858 | 约20到50倍 |
| 性能提升 | 1 | 约1.2到2倍 |
后话
其实,这种基本的简单操作并不需要花这么多心思去做性能优化,目前的计算设备性能也越来越好,程序中需要性能的核心部分(比如游戏引擎),一般都是用优化的算法,搭配合适的硬件,用C++或者Go语言编写的。有时候为了追求性能甚至可以牺牲可读性和维护性。
做这个小题的性能优化,只是希望用一个小的引子,告诉大家做程序开发不仅仅只是实现功能就完事了。稍微多花一点点心思去多想多做,就会收获很不一样的性能结果,而这些优化和提升,正是软件工程师的价值所在。

 随时随地看视频
随时随地看视频




