I. 奇异值分解(Singular Value Decomposition)

1. 定义

Singular Value Decomposition (SVD)是线性代数中十分重要的矩阵分解方法，被称为“线性代数的基本理论”，因为它不仅可以运用于所有矩阵(不像特征值分解只能用于方阵)，而且奇异值总是存在的。

SVD定理
设一个矩阵Am×nAm×n的秩为r∈[0,min(m,n)]r∈[0,min(m,n)],矩阵AA的奇异值分解形式如下:
A=UΣVT(1.1.1)(1.1.1)A=UΣVT

其中U∈Rm×mU∈Rm×m是一个正交矩阵(即列向量ui,i=1,...,mui,i=1,...,m互相正交)，V∈Rn×nV∈Rn×n也是一个正交矩阵(即列向量vi,i=1,...,nvi,i=1,...,n互相正交),ΣΣ是一个m×nm×n的矩阵，且满足
Σii=σi≥0Σij=0,i≠jΣii=σi≥0Σij=0,i≠j

上面的σiσi称为奇异值(singular values),uiui称为左奇异值(left-singular values),vivi称为右奇异值(right-singular values)。另外通常默认有σ1≥...≥σr≥0σ1≥...≥σr≥0。

注意：矩阵AA是一个长方形矩阵，不一定是方阵，另外ΣΣ和矩阵AA的维度相同，并且其包含一个对角子矩阵(diagonal submatrix)。

对于奇异值分解可以从两个角度进行理解：一是将SVD视为对基向量组(bases)，即坐标系的一顺序变换，二是将SVD视为对于数据点的变换。

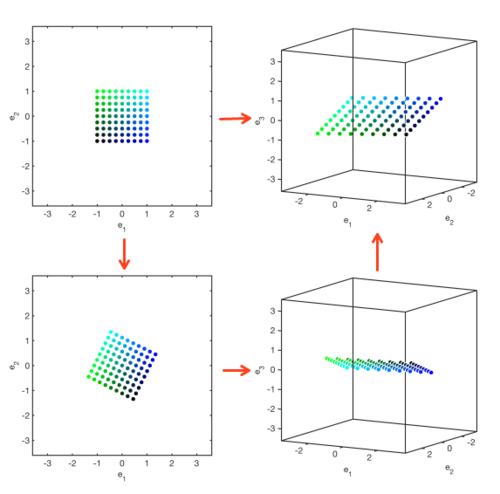
一般来说要让矩阵AA作用于另一个矩阵，都是左乘AA,所以由公式(1)可知道首先是VTVT，然后是ΣΣ,最后是矩阵UU变换。所以矩阵AA的变换实际上是经过了三个步骤，如下图所示(为方便理解使用了二维和三维图像进行说明)：

假设左上角的单位圆是在RnRn空间，其标准基用B=[v1,v2]B=[v1,v2]表示。左下角的圆也在RnRn空间里，其标准基用B~=[e1,e2]B~=[e1,e2]表示，右下角的圆在RmRm空间里，其标准基用C~C~表示。右上角的圆在RmRm空间里。

由左上角到左下角：可以很清楚的看到VT∈Rn×nVT∈Rn×n的作用是对最开始的坐标轴(或标准基)(BB)还原成canonical basis(B~B~)。所以VTVT的作用是将坐标轴由BB转变成B~B~。
由左下角到右下角：经过ΣΣ矩阵变换后从RnRn空间转换到了RmRm空间。上图是从二维空间变成了三维空间，即增加了z轴。当然维度也可以减少。此外单位圆还是处在[e1,e2][e1,e2]空间内(即x,yx,y轴组成的空间内)，而且还会根据奇异值的大小做相应比例的伸缩。
右下角到右上角: 矩阵UU继续对[e1,e2][e1,e2]基做变换，增加的那个维度(z轴)方向不做变化。

下图更加形象地展示了奇异值分解的作用，变换过程和上面一样，故不再赘述：

本小节内容不证明SVD的存在性。

在介绍SVD如何计算之前，首先回顾一下【Math for ML】矩阵分解(Matrix Decompositions) （下）中介绍过任何对称矩阵都能对角化，其公式如下：

S=ST=PDPTS=ST=PDPT

所以一个对称矩阵的奇异值分解是十分相似的，即

S=UΣVTS=UΣVT

对比之后可知有U=P,V=P,Σ=DU=P,V=P,Σ=D

另外我们还需要知道的是对于任意矩阵A∈Rm×nA∈Rm×n,其转置矩阵和其本身相乘之后得到的矩阵都是对称矩阵，即ATA∈Rn×nATA∈Rn×n和AAT∈Rm×mAAT∈Rm×m均为对称矩阵。(证明略)

接下来结合SVD公式给出对任意矩阵A∈Rm×nA∈Rm×nSVD计算的推导过程：

已知ATAATA可作如下对角化运算，且其特征值λi≥0λi≥0

ATA=PDPT=Pλ1⋮0⋯⋱⋯0⋮λnPT(1.3.1)(1.3.1)ATA=PDPT=P[λ1⋯0⋮⋱⋮0⋯λn]PT

因为任何矩阵都可做奇异值分解，故有

ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT(1.3.2)(1.3.2)ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT

因为UU为正交矩阵，所以UTU=IUTU=I,所以(1.3.2)式进一步简化可得

ATA=VΣTΣVT=Vσ21⋮0⋯⋱⋯0⋮σ2nVT(1.3.3)(1.3.3)ATA=VΣTΣVT=V[σ12⋯0⋮⋱⋮0⋯σn2]VT

由(1.3.1)和(1.3.3)可得

V=Pσ2i=λi(1.3.4)(1.3.4)V=Pσi2=λi

所以任意矩阵AA的右奇异矩阵VV是ATAATA的特征矩阵PP。

和求VV类似，这里不再赘述。UU即为AATAAT的特征矩阵。

注意上面两步中已经求出了σ2iσi2,接下来要做的就是把上面所求出的σ2iσi2从大到小排序并开根号，且ΣΣ要与AA的维度保持一致

下面对特征值分解A=PDP−1A=PDP−1和奇异值分解A=UΣVTA=UΣVT作如下总结和对比：

SVD对于任意矩阵都存在；而EVD只能在n阶方阵的基础上才能被定义，而且只有当方阵满秩，即有n个独立的特征向量条件下才可以做特征值分解；
特征值分解后得到的矩阵PP不必须是正交矩阵，也就是说PP可以起到伸缩和旋转的作用；而SVD中的U,VU,V矩阵都必须是正交矩阵，所以这两个矩阵只能起到旋转变换的作用，起伸缩变换作用的是矩阵ΣΣ。
特征值分解和奇异值分解都由以下三个线性映射步骤组成：
1.Change of basis in the domain
2.Independent scaling of each new basis vector and mapping from domain to co-domain
3.Change of basis in the co-domain