java.lang.Object java.util.Collections简介
此类仅包含操作或返回集合的静态方法。
它包含多样的对集合进行操作的算法,“包装器”,返回由指定集合支持的新集合,以及其他一些细碎功能。
如果提供给它们的集合或类对象为null,则此类的方法都抛出NullPointerException
该类中包含的多态算法的文档通常包括实现的简要说明 。 这些描述应被视为实现说明 ,而不是说明的一部分 。 只要规范本身得到遵守,实现者就可以随意替代其算法。 (例如,sort使用的算法不一定是一个mergesort,但它必须是稳定的 算法)
如果集合不支持适当的突变原语,例如set方法,则该类中包含的“破坏性”算法,即修改其操作的集合的算法被指定为抛出UnsupportedOperationException。 如果调用对集合没有影响,这些算法可能但不是必须抛出此异常。 例如,在已经排序的不可修改列表上调用sort方法可以抛出UnsupportedOperationException
Collections的sort方法代码:

一

二
<T extends Comparable<? super T>> 表示该方法中传递的泛型参数必须实现了Comparable中的compareTo(T o)方法,否则进行不了sort排序
其sort方法实现都委托给了java.util.List接口的默认实现的sort方法

方法细节奏:
(1)将list转换成一个Object数组
(2)将这个Object数组传递给Arrays类的sort方法(也就是说Collections的sort本质是调用了Arrays.sort)
(3)完成排序之后,再一个一个地,把Arrays的元素复制到List中
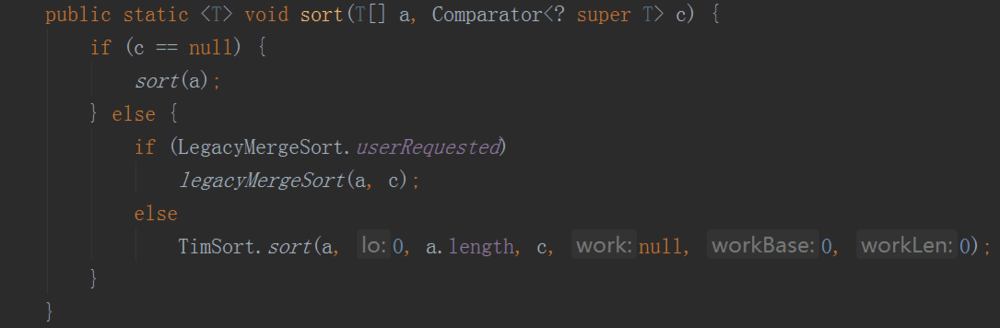
注意到sort有一个条件判断,
当
LegacyMergeSort.userRequested==true,采用legacyMergeSort否则采用ComparableTimSort
LegacyMergeSort.userRequested的字面意思大概就是“用户请求传统归并排序”,这个分支调用的是与jdk5相同的方法来实现功能。
ComparableTimSort是改进后的归并排序,对归并排序在已经反向排好序的输入时表现为O(n^2)的特点做了特别优化。对已经正向排好序的输入减少回溯。对两种情况(一会升序,一会降序)的输入处理比较好(摘自百度百科)。
legacyMergeSort代码:
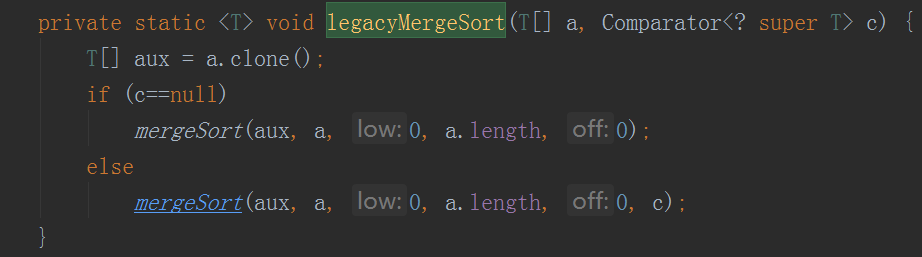
泛型版
mergeSort代码

①:对dest[]排序,传递过来的List<T> list也就排好了序,src[]数组用做中介,即后面的方法需要调用,这里有个判断条件为length < INSERTIONSORT_THRESHOLDINSERTIONSORT_THRESHOLD为Arrays的一个常量7,它定义了如果数组元素小于7用插入排序
②:当数组元素不小于7,先将数组拆分成低区间和高区间
再调用两个递归对区间元素排序。在递归时注意还会判断已划分区间元素是否还不少于7,如果不小于7继续划分成两个区间,这样循环递归调用
特别注意src[]和dest[]的参数位置,调用递归时,是将src[]数组作为排序对象进行排序,src[]排序后,在通过③或④方法将dest[]数组依据src进行排序。最终达到List<T> list排序的结果。
③:如果初始元素个数不小于7进过②方法后,只有两种情况:两个排好序的低区间和高区间。这个方法作用是:
如果低区间列表中的最高元素小于高区间列表中的最低元素,则表明该次递归循环的区间段已经排好序,然后将这段数据复制到dest[]数组中。
反之则进入方法④
④:进入该方法表明该次递归循环的左区间最大元素大于右区间最小元素,也就是说左区间的数组元素值都大于高区间的数组元素值,因此将src中的高区间元素和低区间元素调换放入dest数组中。这样一次递归循环就调用完毕,如果还有循环就继续排序下去,否则排序就已经完成。
TimSort.sort()
/*
* The next method (package private and static) constitutes the
* entire API of this class.
*/
/**
* Sorts the given range, using the given workspace array slice
* for temp storage when possible. This method is designed to be
* invoked from public methods (in class Arrays) after performing
* any necessary array bounds checks and expanding parameters into
* the required forms.
*
* @param a the array to be sorted
* @param lo the index of the first element, inclusive, to be sorted
* @param hi the index of the last element, exclusive, to be sorted
* @param c the comparator to use
* @param work a workspace array (slice)
* @param workBase origin of usable space in work array
* @param workLen usable size of work array
* @since 1.8
*/
static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
T[] work, int workBase, int workLen) { assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length; int nRemaining = hi - lo; if (nRemaining < 2) return; // Arrays of size 0 and 1 are always sorted
//待排序的个数如果小于32(MIN_MERGE),使用不归并的迷你版timsort二分排序
if (nRemaining < MIN_MERGE) { int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
binarySort(a, lo, hi, lo + initRunLen, c); return;
} /**
* March over the array once, left to right, finding natural runs,
* extending short natural runs to minRun elements, and merging runs
* to maintain stack invariant.
*/
TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen); int minRun = minRunLength(nRemaining); do { // Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi, c); // If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) { int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen, c); // 对[lo,lo+force]排好序了,当然下次的 run length 长度是force
runLen = force;
} // 把这次run的基点位置和长度压栈,必要时合并
ts.pushRun(lo, runLen); // TimSort持有数组a,根据区间来合并,从而达到排序
ts.mergeCollapse(); // Advance to find next run 准备下一轮的部分排序
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0); // Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse(); assert ts.stackSize == 1;
}(1)传入的待排序数组若小于阈值MIN_MERGE(Java实现中为32,Python实现中为64),则调用 binarySort,这是一个不包含合并操作的 mini-TimSort。
a) 从数组开始处找到一组连接升序或严格降序(找到后翻转)的数
b) Binary Sort:使用二分查找的方法将后续的数插入之前的已排序数组,binarySort对数组a[lo:hi]进行排序,并且a[lo:start]是已经排好序的。算法的思路是对a[start:hi]中的元素,每次使用binarySearch为它在a[lo:start]中找到相应位置,并插入。
(2)开始真正的TimSort过程:
(2.1) 选取minRun大小,之后待排序数组将被分成以minRun大小为区块的一块块子数组
a) 如果数组大小为2的N次幂,则返回16(MIN_MERGE / 2)
b) 其他情况下,逐位向右位移(即除以2),直到找到介于16和32间的一个数
minRun
private static int minRunLength(int n) {
assert n >= 0;
int r = 0; // Becomes 1 if any 1 bits are shifted off
while (n >= MIN_MERGE) {
r |= (n & 1);
n >>= 1;
}
return n + r;
}这个函数根据 n 计算出对应的 natural run 的最小长度。MIN_MERGE 默认为32,如果n小于此值,那么返回n 本身。否则会将 n 不断地右移,直到少于 MIN_MERGE,同时记录一个 r 值,r 代表最后一次移位n时,n最低位是0还是1。 最后返回 n + r,这也意味着只保留最高的 5 位,再加上第六位。
(2.2)do-while
(2.2.1)找到初始的一组升序数列,countRunAndMakeAscending 会找到一个run ,这个run 必须是已经排序的,并且函数会保证它为升序,也就是说,如果找到的是一个降序的,会对其进行翻转。
(2.2.2)若这组区块大小小于minRun,则将后续的数补足,利用binarySort 对 run 进行扩展,并且扩展后,run 仍然是有序的。
(2.2.3)当前的 run 位于 a[lo:runLen] ,将其入栈ts.pushRun(lo, runLen);//为后续merge各区块作准备:记录当前已排序的各区块的大小
(2.2.4)对当前的各区块进行merge,merge会满足以下原则(假设X,Y,Z为相邻的三个区块):
a) 只对相邻的区块merge
b) 若当前区块数仅为2,If X<=Y,将X和Y merge
b) 若当前区块数>=3,If X<=Y+Z,将X和Y merge,直到同时满足X>Y+Z和Y>Z
由于要合并的两个
run是已经排序的,所以合并的时候,有会特别的技巧。假设两个run是run1,run2,先用gallopRight在run1里使用binarySearch查找run2 首元素的位置k, 那么run1中k前面的元素就是合并后最小的那些元素。然后,在run2中查找run1 尾元素的位置len2,那么run2中len2后面的那些元素就是合并后最大的那些元素。最后,根据len1与len2大小,调用mergeLo或者mergeHi将剩余元素合并。
(2.2.5) 重复2.2.1 ~ 2.2.4,直到将待排序数组排序完
(2.2.6) Final Merge:如果此时还有区块未merge,则合并它们
(3)示例
注意:为了演示方便,我将TimSort中的minRun直接设置为2,否则我不能用很小的数组演示。。。同时把MIN_MERGE也改成2(默认为32),这样避免直接进入binary sort。
初始数组为[7,5,1,2,6,8,10,12,4,3,9,11,13,15,16,14]
=> 寻找连续的降序或升序序列 (2.2.1),同时countRunAndMakeAscending函数会保证它为升序
[1,5,7] [2,6,8,10,12,4,3,9,11,13,15,16,14]=> 入栈 (2.2.3)
当前的栈区块为[3]=> 进入merge循环 (2.2.4)
do not merge因为栈大小仅为1=> 寻找连续的降序或升序序列 (2.2.1)
[1,5,7] [2,6,8,10,12] [4,3,9,11,13,15,16,14]=> 入栈 (2.2.3)
当前的栈区块为[3, 5]=> 进入merge循环 (2.2.4)
merge因为runLen[0]<=runLen[1]
gallopRight:寻找run1的第一个元素应当插入run0中哪个位置(”2”应当插入”1”之后),然后就可以忽略之前run0的元素(都比run1的第一个元素小)
gallopLeft:寻找run0的最后一个元素应当插入run1中哪个位置(”7”应当插入”8”之前),然后就可以忽略之后run1的元素(都比run0的最后一个元素大) 这样需要排序的元素就仅剩下[5,7] [2,6],然后进行mergeLow
完成之后的结果:
[1,2,5,6,7,8,10,12] [4,3,9,11,13,15,16,14]=> 入栈 (2.2.3)
当前的栈区块为[8]
退出当前merge循环因为栈中的区块仅为1=> 寻找连续的降序或升序序列 (2.2.1)
[1,2,5,6,7,8,10,12] [3,4] [9,11,13,15,16,14]
=> 入栈 (2.2.3)
当前的栈区块大小为[8,2]=> 进入merge循环 (2.2.4)
do not merge因为runLen[0]>runLen[1]=> 寻找连续的降序或升序序列 (2.2.1)
[1,2,5,6,7,8,10,12] [3,4] [9,11,13,15,16] [14]=> 入栈 (2.2.3)
当前的栈区块为[8,2,5]=>
do not merege run1与run2因为不满足runLen[0]<=runLen[1]+runLen[2]
merge run2与run3因为runLen[1]<=runLen[2]
gallopRight:发现run1和run2就已经排好序
完成之后的结果:
[1,2,5,6,7,8,10,12] [3,4,9,11,13,15,16] [14]=> 入栈 (2.2.3)
当前入栈的区块大小为[8,7]
退出merge循环因为runLen[0]>runLen[1]=> 寻找连续的降序或升序序列 (2.2.1)
最后只剩下[14]这个元素:[1,2,5,6,7,8,10,12] [3,4,9,11,13,15,16] [14]=> 入栈 (2.2.3)
当前入栈的区块大小为[8,7,1]=> 进入merge循环 (2.2.4)
merge因为runLen[0]<=runLen[1]+runLen[2]
因为runLen[0]>runLen[2],所以将run1和run2先合并。(否则将run0和run1先合并)
gallopRight & 2) gallopLeft
这样需要排序的元素剩下[13,15] [14],然后进行mergeHigh
完成之后的结果:
[1,2,5,6,7,8,10,12] [3,4,9,11,13,14,15,16] 当前入栈的区块为[8,8]=>
继续merge因为runLen[0]<=runLen[1]
gallopRight & 2) gallopLeft
需要排序的元素剩下[5,6,7,8,10,12] [3,4,9,11],然后进行mergeHigh
完成之后的结果:
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] 当前入栈的区块大小为[16]=>
不需要final merge因为当前栈大小为1=>
结束
先看看run的定义,翻译成趋向?一个run是从数组给定位置开始的最长递增或者递减序列的长度,为了得到稳定的归并排序,这里的降序中使用的“>”,不包含"=",保证stability。原注释是:

具体计算最长run长度:
private static <T> int countRunAndMakeAscending(T[] a, int lo, int hi,
Comparator<? super T> c) { assert lo < hi; int runHi = lo + 1; if (runHi == hi) return 1; // Find end of run, and reverse range if descending
if (c.compare(a[runHi++], a[lo]) < 0) { // Descending
while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) < 0)
runHi++; // 如果是递减序列,那么就得到最长的,然后逆序
reverseRange(a, lo, runHi);
} else { // Ascending
while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) >= 0)
runHi++;
} return runHi - lo; // 这个run的最大长度}举个例子吧,如下图:

排序小数组
获得初始的run长度后,调用 binarySort(a, lo, hi, lo + initRunLen, c),binarySort 当然不会浪费时间再去排序在求run长度时已经排好序的头部(lo->start),然后进行二分插入排序。
binarySort要做的就是把后续的元素依次插入到属于他们的位置,基点就是已经排好序的子数组(如果没有的子数组就是首元素),把当前操作的元素称为pivot,通过二分查找,找到自己应该插入的位置(达到的状态是left==right),找到位置后,就要为pivot的插入腾出空间,所以需要元素的移动,代码中如果移动少于两个元素就直接操作,否则调用System.arraycopy(),最后插入我们的pivot到正确的位置。
这样我想到了之前在学习排序的时候的几个算法,其中有个说法是,对于小数组的排序使用插入排序,大数组的时候使用快排,归并排序之类的。
/**
* Sorts the specified portion of the specified array using a binary
* insertion sort. This is the best method for sorting small numbers
* of elements. It requires O(n log n) compares, but O(n^2) data
* movement (worst case).
*
*/private static <T> void binarySort(T[] a, int lo, int hi, int start,
Comparator<? super T> c) { assert lo <= start && start <= hi; if (start == lo)
start++; for ( ; start < hi; start++) {
T pivot = a[start]; // Set left (and right) to the index where a[start] (pivot) belongs
int left = lo; int right = start; assert left <= right; /*
* Invariants: 排序过程的不变量
* pivot >= all in [lo, left).
* pivot < all in [right, start).
*/
while (left < right) { int mid = (left + right) >>> 1;
// 二分查找找到属于pivot的位置
if (c.compare(pivot, a[mid]) < 0)
right = mid; else
left = mid + 1;
} assert left == right; /*
* The invariants still hold: pivot >= all in [lo, left) and
* pivot < all in [left, start), so pivot belongs at left. Note
* that if there are elements equal to pivot, left points to the
* first slot after them -- that's why this sort is stable.
* Slide elements over to make room for pivot.
*/
int n = start - left; // The number of elements to move
// Switch is just an optimization for arraycopy in default case
switch (n) { // 移动元素
case 2: a[left + 2] = a[left + 1]; case 1: a[left + 1] = a[left]; break; default: System.arraycopy(a, left, a, left + 1, n);
} // 属于自己的位置
a[left] = pivot;
}
}排序大数组
接下来看如果待排序的个数>=32时的过程,首先弄明白minRunLength得到的是什么。注释很清楚,虽然理论基础不理解。
* Roughly speaking, the computation is: * * If n < MIN_MERGE, return n (it's too small to bother with fancy stuff). * Else if n is an exact power of 2, return MIN_MERGE/2.* Else return an int k, MIN_MERGE/2 <= k <= MIN_MERGE, such that n/k * is close to, but strictly less than, an exact power of 2.
如果还是很抽象的话,从32到100得到的min run length如下,可以直观的体会下:
16,17,17,18,18,19,19,20,20,21,21,22,22,23,23,24,24,25,25,26,26,27,27,28,28,29,29,30,30,31,31,32,16,17,17,17,17,18,18,18,18,19,19,19,19,20,20,20,20,21,21,21,21,22,22,22,22,23,23,23,23,24,24,24,24,25,25,25
得到 minRun 之后,取 minRun 和 nRemaining 的最小值作为这次要排序的序列,初始的有序数组和前面情况(1)的获取方式一样,然后做一次二分插入排序,现在有序序列的长度是force,这一部分排好序之后,把本次run的起始位置和长度存入一个stack中(两个数组),后续就是根据这些区间完成排序的。每次push之后就是要进行合并检查,也就是说相邻的区间能合并的就合并,具体的:
/**
* Examines the stack of runs waiting to be merged and merges adjacent runs
* until the stack invariants are reestablished:
*
* 1\. runLen[i - 3] > runLen[i - 2] + runLen[i - 1]
* 2\. runLen[i - 2] > runLen[i - 1]
*
* This method is called each time a new run is pushed onto the stack,
* so the invariants are guaranteed to hold for i < stackSize upon
* entry to the method.
*/private void mergeCollapse() { while (stackSize > 1) { int n = stackSize - 2; if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) { if (runLen[n - 1] < runLen[n + 1])
n--;
mergeAt(n);
} else if (runLen[n] <= runLen[n + 1]) {
mergeAt(n);
} else { break; // Invariant is established
}
}
}我的理解下,虽然每次run之后都能进行合并,但是为了减少合并带来的开销,找到了某种规则,可以在某些条件下避免合并。接下来看看具体合并时的动作。
合并有序区间
有一种情况是:如果前一个区间的长度小于当前区间长度,就进行merge,每个区间是一个排好序的数组,现在要合并第i和i+1个区间。
首先把 run length更新到 ruLen[i] 中,删掉 i+1 的run信息;接下来定位区间2的最小元素在有序区间1的插入位置,更新区间1的 run base 和 run length,称更新后的为区间1'; 然后查找区间1'的最大元素在区间2的正确定位;此时此刻这个数组已经得到了有效的划分,如下图,只需要合并[base1,len1]和[base2,len2]就可以了,其他段已经在正确位置。
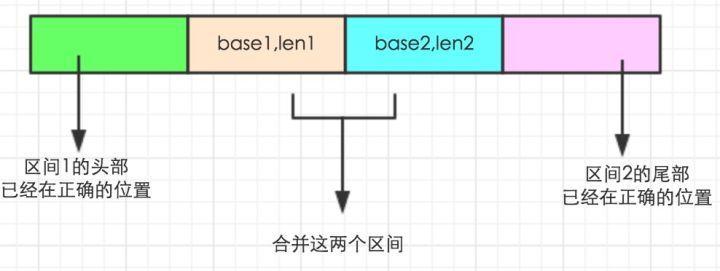
image
private void mergeAt(int i) { assert stackSize >= 2; assert i >= 0; assert i == stackSize - 2 || i == stackSize - 3; int base1 = runBase[i]; int len1 = runLen[i]; int base2 = runBase[i + 1]; int len2 = runLen[i + 1]; assert len1 > 0 && len2 > 0; assert base1 + len1 == base2; /*
* (1) 合并了 i,i+1, 把i+2的信息移动到之前i+1的位置,就是删除i+1
* Record the length of the combined runs; if i is the 3rd-last
* run now, also slide over the last run (which isn't involved
* in this merge). The current run (i+1) goes away in any case.
*/
runLen[i] = len1 + len2; if (i == stackSize - 3) {
runBase[i + 1] = runBase[i + 2];
runLen[i + 1] = runLen[i + 2];
}
stackSize--; /*
*(2)找到区间2的最小元素若插入到区间的话,正确索引位置
* Find where the first element of run2 goes in run1\. Prior elements
* in run1 can be ignored (because they're already in place).
*/
int k = gallopRight(a[base2], a, base1, len1, 0, c); assert k >= 0;
base1 += k;
len1 -= k; // 说明区间2的最小元素在区间1的末尾,所以完成两个区间的合并排序
if (len1 == 0) return; /*
* (3)查找区间1'的最大元素在区间2的正确定位
* Find where the last element of run1 goes in run2\. Subsequent elements
* in run2 can be ignored (because they're already in place).
*/
len2 = gallopLeft(a[base1 + len1 - 1], a, base2, len2, len2 - 1, c); assert len2 >= 0; // 说明区间1'的最大元素小于区间2的最小元素,所以完成排序
if (len2 == 0) return; // Merge remaining runs, using tmp array with min(len1, len2) elements
if (len1 <= len2)
mergeLo(base1, len1, base2, len2); else
mergeHi(base1, len1, base2, len2);
}为了性能,在len1<=len2的时候使用mergeLo,len1>=len2的时候使用mergeHi,通过前面的定位,到这里的时候,有a[base1]>a[base2],a[base1+len1]<a[base2+len2],合并后,最终完成了排序。
作者:芥末无疆sss
链接:https://www.jianshu.com/p/1efc3aa1507b
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。

 随时随地看视频
随时随地看视频



