一.概念
1.1贝叶斯定理:假设H[1],H[2]…,H[n]互斥且构成一个完全事件,已知它们的概率P(H[i]),i=1,2,…,n,现观察到某事件A与H[1],H[2]…,H[n]相伴随机出现,且已知条件概率P(A/H[i]),求P(H[i]/A)。即:已知某条件概率P(A|B),其交换事件P(B|A) = P(A|B)P(B)/P(A)【注:P(A|B)表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:P(A|B)=P(AB)/P(B)】
1.2朴素贝叶斯: 对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。所以程序里主要的工作就是计算出各个条件概率。
二.阶段
整个朴素贝叶斯分类分为三个阶段:
①准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
②分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
③应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
三.实现
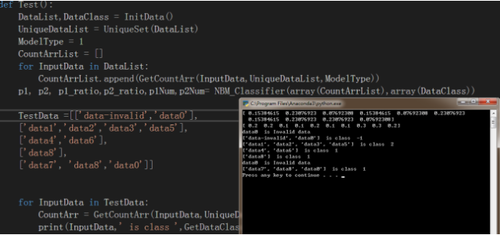
#coding=utf-8from numpy import *#初始化数据#DataList 多条样例数据#DataClass 数据对应的分类def InitData():DataList=[['data8'],['data1', 'data2', 'data3', 'data4'],['data1', 'data2', 'data5', 'data6'],['data1', 'data2', 'data4', 'data6'],['data8', 'data9'],['data7', 'data8'],['data1', 'data2'],['data-invalid']]DataClass = [1,1,2,1,2,1,2,0]return DataList,DataClass#去除重复数据#UniqueSet 无重复的数据集def UniqueSet(DataSet):UniqueSet = set([])for i in DataSet:UniqueSet = UniqueSet | set(i)#set并return list(UniqueSet)#数据状态压缩#InputData 输入数据#DataSet 数据集#ModelType 模型类别 1:只考虑存不存在 2:考虑出现次数……#CountArr 数据状态数组def GetCountArr(InputData,DataSet,ModelType):CountArr = [0] * len(DataSet)for i in InputData:if i in DataSet:if ModelType == 1:CountArr[DataSet.index(i)] = 1else:CountArr[DataSet.index(i)] += 1else:print(i,' is Invalid data')return array(CountArr)#朴素贝叶斯分类器 #CountArrList 数据状态集#DataClass 数据类别#p1 p1概率自然对数#p2 p2概率自然对数#p1_ratio 数据集p1占比#p2_ratio 数据集p2占比#p1Num 数据集影响p1的数量#p2Num 数据集影响p2的数量def NBM_Classifier(CountArrList,DataClass):ListLen = len(CountArrList)WordsLen = len(CountArrList[0])p1_ratio = (sum(DataClass==1))/float(ListLen)p2_ratio = (sum(DataClass==2))/float(ListLen)#某分类下某词项出现频次为0时,其概率也是0,#因此在计算p(w0|ci)p(w1|ci)p(w2|ci)......p(wN|ci)会因为其中某个的概率为0而全部是0。 #为了避免这样的情况发生,我们将所有词项出现的频次都初始化为1,某类所有词项数量初始化为2。p1Num = ones(WordsLen)p2Num = ones(WordsLen)p1Denom = 2.0p2Denom = 2.0for i in range(ListLen):if DataClass[i] == 1:p1Num +=CountArrList[i]p1Denom += sum(CountArrList[i])elif DataClass[i] == 2:p2Num +=CountArrList[i]p2Denom += sum(CountArrList[i])#由于p(w0|ci)p(w1|ci)p(w2|ci)......p(wN|ci)中每个因子都很小#所有因子相乘,特别是因子数量多的时候,会导致结果溢出,从而得到错误的数据 #为了避免溢出问题的发生,使用求自然对数的方法#自然对数和原本的数值同增同减,不会有任何损失,因此不会影响求得的概率结果。print(p1Num/p1Denom)print(p2Num/p2Denom)p1 = log(p1Num/p1Denom)p2 = log(p2Num/p2Denom)return p1,p2,p1_ratio,p2_ratio,p1Num-1,p2Num-1#获取数据类别#CountArr 数据状态数组#p1 p1概率自然对数#p2 p2概率自然对数#p1_ratio 数据集p1占比#p2_ratio 数据集p2占比#p1Num 数据集影响p1的数量#p2Num 数据集影响p2的数量def GetDataClass(CountArr, p1, p2, p1_ratio,p2_ratio,p1Num,p2Num):#无效数据:该数据没有影响过p1和p2if sum(CountArr*p1Num) == 0 and sum(CountArr*p2Num) == 0:return -1#数学公式:ln(a*b)=ln(a) +ln(b)is_p1 = sum(CountArr * p1) + log(p1_ratio)is_p2 = sum(CountArr * p2) + log(p2_ratio)if is_p1 > is_p2:return 1else:return 2 def Test():DataList,DataClass = InitData()UniqueDataList = UniqueSet(DataList)ModelType = 1CountArrList = []for InputData in DataList:CountArrList.append(GetCountArr(InputData,UniqueDataList,ModelType))p1, p2, p1_ratio,p2_ratio,p1Num,p2Num= NBM_Classifier(array(CountArrList),array(DataClass))TestData =[['data-invalid','data0'],['data1','data2','data3','data5'],['data4','data6'],['data8'],['data7', 'data8','data0']]for InputData in TestData:CountArr = GetCountArr(InputData,UniqueDataList,ModelType)print(InputData,' is class ',GetDataClass(CountArr,p1,p2,p1_ratio,p2_ratio,p1Num,p2Num))Test()
四.贝叶斯网络
把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
贝叶斯网络是一种概率网络,它是基于概率推理的图形化网络,而贝叶斯公式则是这个概率网络的基础。一个贝叶斯网络是一个有向无环图(Directed Acyclic Graph,DAG),由代表变量节点及连接这些节点有向边构成。节点代表随机变量,节点间的有向边代表了节点间的互相关系(由父节点指向其子节点),用条件概率进行表达关系强度,没有父节点的用先验概率进行信息表达。节点变量可以是任何问题的抽象,如:测试值,观测现象,意见征询等。适用于表达和分析不确定性和概率性的事件,应用于有条件地依赖多种控制因素的决策,可以从不完全、不精确或不确定的知识或信息中做出推理。连接两个节点的箭头代表此两个随机变量是具有因果关系(或非条件独立)。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。每个结点在给定其直接前驱时,条件独立于其非后继。
五.概率图模型
隐马尔可夫模型(HMM):马尔可夫过程与未观测到的(隐藏的)的状态的概率图模型。
通过贝叶斯网络简化形成一条链式模型,Ai+1只与Ai有关,与A1,…,Ai-1无关,称作马尔可夫链,但由于实际大多数问题都不是能够直接观察出来的,而是隐藏在可观察参数后面的未知参数。类似这样的事件马尔可夫链是不能直接解决的,于是延伸出隐马尔可夫模型。隐马尔可夫模型由被观察到的事件涉及到隐藏事件,且这些隐藏事件在概率模型中被我们认为是引导因素。
马尔可夫随机场(MRF):建立在马尔可夫模型和贝叶斯理论基础之上的概率图模型
在随机场的基础上添加马尔科夫性质,从而得到马尔可夫随机场。把马尔科夫随机场映射到无向图中,此无向图中的节点都与某个随机变量相关,连接着节点的边代表与这两个节点有关的随机变量之间的关系,所以,马尔可夫随机场其实表达出随机变量之间有些关系因素是必须要考虑的,而另外则有些是可以不用考虑的。马尔可夫随机场的某个随机变量仅仅只与其相邻的随机变量有关,与那些不相邻的随机变量无关。
条件随机场(CRF):基于遵循马尔可夫性的概率图模型。
结合了最大熵模型和隐马尔可夫模型的特点,是一种无向图模型,条件随机场是一个典型的判别式模型,其联合概率可以写成若干势函数联乘的形式,其中最常用的是线性链条件随机场。若让x=(x1,x2,…xn)表示被观察的输入数据序列,y=(y1,y2,…yn)表示一个状态序列,在给定一个输入序列的情况下,线性链的CRF模型定义状态序列的联合条件概率为
p(y|x)=exp{} (2-14)
Z(x)={} (2-15)
其中:Z是以观察序列x为条件的概率归一化因子;fj(yi-1,yi,x,i)是一个任意的特征函数;是每个特征函数的权值。
六.总结
朴素贝叶斯分类器(Naive Bayes Classifier,或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。
七.相关学习资源
http://blog.csdn.net/moxigandashu/article/details/71480251?locationNum=16&fps=1
https://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

 随时随地看视频
随时随地看视频




