【九月打卡】第10天 Python3入门机器学习

课程名称：Python3入门机器学习 经典算法与应用 入行人工智能
课程章节：8-1;8-2;8-3
主讲老师：liuyubobobo

内容导读

---

• 第一部分 多项式回归的介绍
• 第二部分 多项式代码展示

②课程详细

---

第一部分 多项式回归的介绍

有时候，在进行线性回归的时候会发现，准确率并不是那么的高，并且很难提高，不管是对数据进行怎么样的处理，或者怀疑有没有哪一步重要的没有做到，其实有时候是前提条件出错了，线性回归的前提条件是，假设数据是线性的，但有时候数据并不是线性的，比如：

从肉眼来看这个数据就是一个二次曲线，用线性的方式当然难以拟合成功
，假如使用线性回归就会变成这个样子，

所以这里就可以引入多项式回归！！
多项式回归是在数据处理前进行的，简单来说，通过对数据的升维，来达到变复杂的效果，但是升维的数据与原始数据呈一定关系，所以可以在二维层面展示拟合结果，下面展示代码，与sklearn中方便调用的方法。

第二部分 多项式代码展示

导入函数

import numpy as np
import matplotlib.pyplot as plt

创建X

X = np.random.uniform(-3, 3, size=100)
X = X.reshape(-1, 1)

创建y

y = 0.5 * X**2 + X + 2 + np.random.normal(0, 1, size=100).reshape(-1,1)

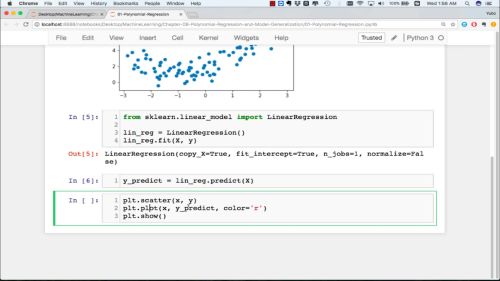
通过线性回归来拟合非线性数据并可视化
导入函数

from sklearn.linear_model import LinearRegression

lin_reg1 = LinearRegression()
lin_reg1.fit(X, y)

预测

y_predict = lin_reg1.predict(X)

可视化

plt.scatter(X, y)
plt.plot(X, y_predict, color='r')
plt.show()

拟合地确实不太好

接下来通过多项式的方式对数据进行预处理
添加一个维度，X2维X1的平方

X2 = np.concatenate([X, X**2],axis=1)
X2.shape

进行预测

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

可视化预测结果

plt.scatter(X, y)
plt.plot(np.sort(X, axis=0), y_predict2[np.argsort(X, axis=0)].reshape(-1,1), color='r')
plt.show()

是理想的结果

③课程思考

---

线性回归算法的局限性: 需要有线性关系
多项式回归对非线性数据进行处理，使用线性回归思路，为原来的数据样本添加新的特征，而得到新的特征方式是原有特征方式的多项式组合，采用这样的方式可以解决非线性问题，PCA做降维，而多项式回归则让数据集升维，添加新的数据特征，使得算法更好拟合高维度数据。
这就是这节介绍多项式回归的原因，用于处理不是线性的数据

④课程截图

---