在上一篇文章中,我们通过最小二乘法得到了线性回归问题中,最优参数的闭式解:
但是为什么在优化时使用最小二乘法呢?
从正态分布到最小二乘法
在这一小节,我们重点阐述所有推导的依据,首先要给出一个关键的定理,中心极限定理,作为后续的基础。
中心极限定理
中心极限定理说明大量的独立同分布变量共同作用的结果,会逐渐趋近一个正态分布,我们可以认为,也是假设预测值和真实值之间的误差ϵ\epsilonϵ,来源于大量的独立同分布(iid, independently identically distribution)效果的叠加,这里的独立来源于不同干扰项之间相互不影响,但是同分布的要求较为牵强,可认为是由于产生的环境都较为类似故近似认为是同分布,但是正态分布的常见性使得这个假设的适用范围很广,一般会有较好的效果。
可记

满足ϵi∼N (μ,σ2)\epsilon_i \sim \bold{N} ~(\mu, \sigma^2)ϵi∼N (μ,σ2),其中β\betaβ为真实参数。
而其中误差的均值可以通过bias调整到零,即将bias项增加μ\muμ,则ϵi=y−xiTβ−μ\epsilon_i = y-x_i^T\beta-\muϵi=y−xiTβ−μ,此时其对应的正态分布变为N(0,σ2)\bold{N}(0, \sigma^2)N(0,σ2),成功将分布中心移到原点处。。
引入了正态分布之后,可以据此进行下一步的讨论。
极大似然估计
使用乘法原理得到如下的联合分布,以描述当前数据集

可认为在类似环境下产生的数据方差一样,即认为ϵi\epsilon_iϵi独立同分布。这个iid的底气就比上面那个假设要强。
则上式取对数之后有
所以最大化上述概率值,等价于最小化∑ϵi2\sum \epsilon_i^2∑ϵi2,即等价于使用最小二乘法进行优化。
至此,我们证明了最小二乘法和正态分布之间的关系,实际上,所有使用mse作为优化指标的任务都默认一个正态分布的先验假设。
显然,ϵ\epsilonϵ和真实值之间的关系可如下表示

即在统计的视角下,给定XXX之后,YYY是一个在预测值附近波动的量,反过来说,给定了数据集即输入输出之后,预测值的出现对应一个概率值,上述的工作就是在最大化这个概率。
这也意味着,在所有的样本中,一个XXX可能对应不同的YYY。
又ϵi\epsilon_iϵi同分布,故其方差为
若YiY_iYi之间没有相关性,则
又由
当ϵi=0\epsilon_i = 0ϵi=0时,意味着输入输出的关系一一对应,否则单一预测值无法同时满足多个不同的输出,此时βls^=β\hat{\beta^{ls}} = \betaβls^=β,是一定值,所以 β^\hat{\beta}β^ 的扰动来源于XXX确定之后YYY的不确定性,有
- E(ϵ)=0E(\epsilon) = 0E(ϵ)=0
- var(x)=σ2I,var(Ax)=Aσ2IATvar(x)=\sigma^2I, var(Ax) = A\sigma^2IA^Tvar(x)=σ2I,var(Ax)=Aσ2IAT
- (XTX)−1XTσ2IX(XTX)−1T=σ2(XTX)−1XTX(XTX)−1T=(XTX)−1σ2(X^TX)^{-1}X^T\sigma^2IX(X^TX)^{-1^T}=\sigma^2(X^TX)^{-1}X^TX(X^TX)^{-1^T}=(X^TX)^{-1}\sigma^2(XTX)−1XTσ2IX(XTX)−1T=σ2(XTX)−1XTX(XTX)−1T=(XTX)−1σ2
综上有

从均方误差到平均值
当我们需要用常数去minimize一个mse时,哪一个会是最合适的数值。
简单的求导看一下。

这是一个凸函数,故令上式为0,则有
即
所以此时使用均值可以得到最小的均方误差。
进一步的,如果使用的绝对值误差,此时的常数对应数据集的中位数,这个结论可以依靠去除绝对值符号时,正号和负号数目相等得到。若存在偶数个,记为2K2K2K个样本,则顺序排列后,第KKK和第K+1K+1K+1个样本之间的任意值都可作为最优解。
进一步结合上述两个小结的内容,其实可以发现,所谓的mse、正态分布和取均值作为最优解,实际上是等价的,这一点在后文说到K-Means时会再次提到。
统计所有出现过的不同输入值XXX,记为Xunique=set(X)X_{unique}=set(X)Xunique=set(X)
遍历集合中的所有元素,则此时,前文所述MSE可改写为

即所有的输入样本,按照取值的不同,可以分为不同的子集,若一共有N=∣Xunique∣N = |X_{unique}|N=∣Xunique∣种不同取值,则一共会划分为NNN个子集。
对应的最优解是在每个子集中,将对应的均值作为预测值。对∀Xj∈Xunique\forall X_j \in X_{unique}∀Xj∈Xunique有

对应上文最小二乘法的思路,此时的概率值也最大。但需要说明的是,由于最小化的是整体的损失,这种pointwise的最优解不一定能拟合得到,由模型和数据的特点决定。
这种pointwise的求均值方式不由得使人想起K近邻算法。
以针对回归问题的K近邻模型为例,记距离输入样本XXX最近的K个样本组成集合neighbourneighbourneighbour,则
和上式相比,唯一的区别在于进行求均值的样本范围不同,线性回归使用和输入取值相同的样本,而K近邻使用输入的一个邻域范围内的样本。
则,当样本密度足够大时,即当每一个样本的位置都落入K个样本时,此时利用最小二乘法求解的线性回归和K近邻等价,最近的K个样本都落在输入样本的位置上,求均值的范围从一个邻域缩小为一个点,也即pointwise。
最大似然估计和不同的统计学派
首先,给定一个表达式

表示在β\betaβ所描述的模型中,事件XXX的概率。
当XXX是变量时,此表达式为条件概率,而β\betaβ变化时,此表达式称为似然函数,给定一组观测,其概率值随着参数的变化而变化,似然函数就是参数β\betaβ的函数。
上文中,给定了XXX,选择最佳的参数值,恰恰与此契合。
以上操作记为极大似然估计(maximum likelihood estimation(MLE)),给出由参数决定的概率值,通过调整参数取值使得当前事件的发生获得最大的概率值,即
当前一共有两种较大的统计学派,频率学派和贝叶斯学派。
-
频率学派
认为未知参数是一个固定的数值,可以进行大量重复实验进行逼近得到。但是这存在一定的局限性,这要求事件可以进行重复实验,一来可能没有重复的条件,二来若观测是对于未来进行预测,则实验也无法进行。
和极大似然估计结合时,由于我们认为参数值固定,需要选择一个确定的值来使得观测到的事件发生的概率最大,这个使得似然函数值最大的参数最有可能是真实的参数值。即
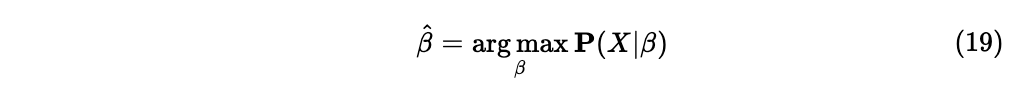
-
贝叶斯学派
贝叶斯学派则认为未知变量是一个满足某种先验分布的随机变量。
综上可知,极大似然估计是一种频率学派的算法,贝叶斯学派有其自身的贝叶斯推断。
用于解释模型的效果指标—R2R^2R2
经过上述的论证,在给定了一个列满秩的XXX和对应的YYY之后,可以利用他们求得当前使得MSE最小的参数β^ls\hat{\beta}^{ls}β^ls。
引入一个新的指标R2R^2R2
其中
接下来对R2R^2R2尝试进行理解
先来看SSTSSTSST,它描述的是所有的输出值之间的方差,即数据的散布情况。
再来看SSESSESSE,它描述的是预测值和真实值之间的差异,模型训练完毕之后,预测值y^\hat{y}y^在真实值yyy的附近发生不可控的震荡,此时SSESSESSE描述了在固定了模型中所有参数的取值之后,剩下的那部分不受控的变化。
减少的量,可理解为输出值减少了多少随机性,在多大的程度上被此时的模型解释。
故,SSTSSTSST描述了数据中输出的方差大小,而SSESSESSE描述了模型训练完毕之后,有多少方差被保留,相应的R2R^2R2实际描述了此模型可以消除,即可以解释多少方差,显然,这个指标越大越好。
还有另一个思路:
当只得到了数据集而未训练得到模型时,若采用mse指标,可使用数据集的均值作为每一个样本的预测值,故此时的方差实际也是对此时预测误差大小的描述。
对应的,式21中的SSE即为模型对每一个样本进行预测所产生的误差之和。
那么R2R^2R2实际也描述了当前模型可以减少多少预测误差,体现了模型的预测能力。
再给出一个在计量统计中常见的统计量
β^ls\hat{\beta}^{ls}β^ls使得凸函数SSE最小,即一阶导数为0,则若记
则有
进一步有
其中intersection
由式25、26,有
又y¯\bar{y}y¯为常数,故
故式27有
因此有

 随时随地看视频
随时随地看视频




