- 优点
- 解决回归问题
- 思想简单,实现容易
- 许多强大的非线性模型的基础(多项式回归,逻辑回归,SVM)
- 结果具有很好的可解释性
- 蕴含机器学习中的很多重要思想
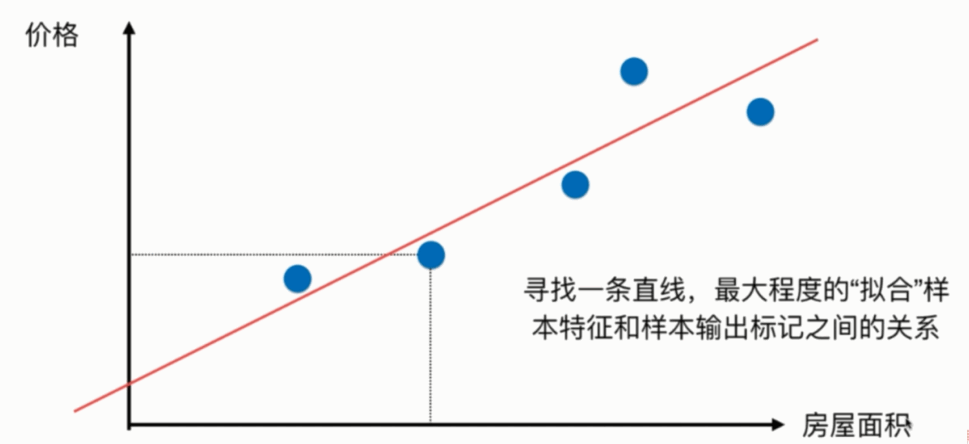
- 上一篇讲K近邻算法时,分类二维平面图横轴纵轴都是样本的特征
- 上图只有横轴是样本的特征,纵轴是样本的输出标记
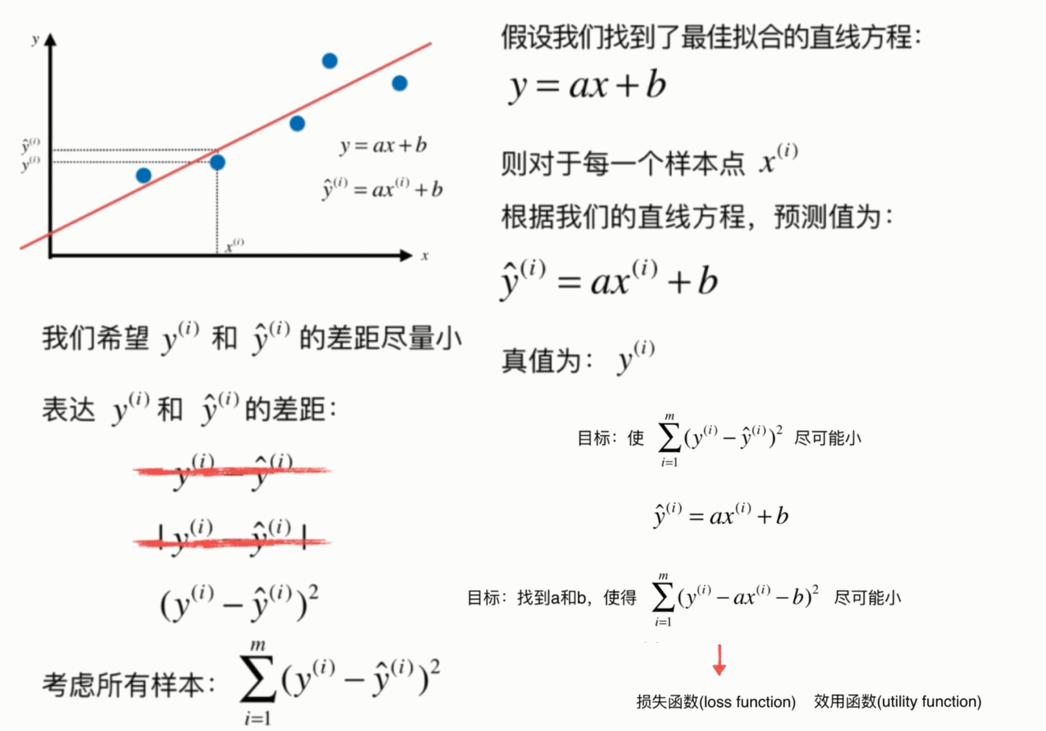
- 通过分析问题,确定问题的损失函数或者效用函数;
- 通过最优化损失函数或者效用函数,获得机器学习的模型。
- 近乎所有参数学习算法都是这样的套路(多项式回归,逻辑回归,SVM,神经网络)->学科:最优化原理->分支:凸优化
最小二乘法
典型的最小二乘法问题:最小化误差的平方

- 简单来说,就是求函数的极值,对函数各个未知分量求导,让导数等于零

向量化
提升大概五十倍的性能
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = 0.0
d = 0.0
for x,y in zip(x_train,y_train):
num += (x-x_mean) * (y - y_mean)
d += (x - x_mean) ** 2
self.a_ = num /d
self.b_ = y_mean - self.a_*x_mean
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = (x_train - x_mean).dot(y_train - y_mean)
d = (x_train - x_mean).dot(x_train - x_mean)
d = 0.0
self.a_ = num /d
self.b_ = y_mean - self.a_*x_mean
衡量指标 MSE,RMS,MAE


最好的指标 R Squared


多元线性回归



- 问题:时间复杂度高:O(n3)(优化O(n2.4)
- 优点:不需要对数据做归一化处理




 随时随地看视频
随时随地看视频




