前面探讨的各种二叉树,使用一个键值在树中导航以执行必要的操作,二叉树中每个节点都有唯一的一个key值,通过key我们可以组织二叉查找树、平衡树、自适应树、堆等,从某种意义上讲,这是一维的二叉树。假如我们现在要研究二维平面上n个点的性质,怎么将它们组织成二叉树呢?如果是3维空间或者k维空间呢?对于一个节点来说,它不仅仅只有一个key值,如果它处于k维空间,那么会有k个key值。我们必须探讨出一种二叉树,可以组织k维空间上的节点。这就是kd二叉树,全称是k-dimension二叉树,k维二叉树。
本文以3维空间为例来探讨kd二叉树的创建、查找、添加、删除。
假设某3维空间上存在7个点,分别是(x1,y2,z3)、(x2,y3,z1)、(x3,y1,z2)、(x4,y4,z4)、(x5,y6,z7)、(x6,y7,z5)、(x7,y5,z6)。其中x(n)<x(n+1),y(n)<y(n+1),z(n)<z(n+1)
创建
如果使用一维二叉查找树来组织以上7个节点,我们可以使用x坐标作为键值(也可以使用y或者z),判断在哪里插入这个点,从而存储所有的点。为了能够独立地使用3个键值,我们组建kd二叉树时可以交替使用x,y,z。在第一层,用x坐标作为识别符号,在第二层,使用y坐标,在第三层,使用z坐标,在第四层继续使用x,以此类推,循环使用3个key值。最终的kd二叉查找树可能是下面这样的:
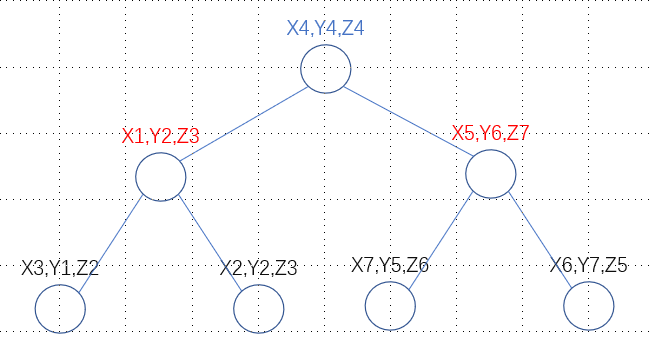
其中,蓝色的是x层,红色的是y层,黑色的是z层。对于x层中的节点P来讲,左子树中任一节点的x的值都小于P节点的x值,右子树中任一节点的x的值都大于P节点的x值。y层和z层同理。
以上的kd二叉查找树是完美平衡的。类似一维二叉查找树,相同的数据流,可以构造出各种各样的二叉查找树。我们希望构造出来的二叉查找树尽可能平衡,平衡意味着在查找数据时可以跳过更多的节点,更加有效率的查找。一维二叉查找树是怎么创建的呢?可以看数据结构与算法-二叉查找树(DSW)。类比其中的创建逻辑,可以探讨出kd二叉树的创建逻辑。
首先,我们决定按照x->y->z的顺序创建kd树,根节点处于x层,那我们将当前7个节点按照x的大小进行排序:
(x1,y2,z3)<(x2,y3,z1)<(x3,y1,z2)<(x4,y4,z4)<(x5,y6,z7)<(x6,y7,z5)<(x7,y5,z6)
取出中间节点(x4,y4,z4)作为根节点,这样做的好处是保证根节点的左右子树节点个数相差不大于1。
第二层是根据节点的y值排序,左子树节点排序如下:
(x3,y1,z2)<(x1,y2,z3)<(x2,y3,z1)
取出中间节点(x1,y2,z3)作为左子树的根节点。
以此类推,可以将右子树以及剩余的节点安插到kd树中,最终,kd树是高度平衡的。
伪代码如下:
def kd_tree(points, depth): if len(points) == 0: return None j = depth mod k 将points数组中节点按照j维度大小排序 获取数组中间节点下标medium_index node = Node(points[medium_index]) node.left = kd_tree(points[:medium_index], depth + 1) node.right = kd_tree(points[medium + 1:], depth +1) return node
伪代码中使用递归来简化逻辑,易于理解,实践中不建议使用。
查找
查找的逻辑比较简单、直观。如果查找(x7,y5,z6),逐层进行比较即可,核心逻辑在于不同层次比较的key值不同。动态图如下:
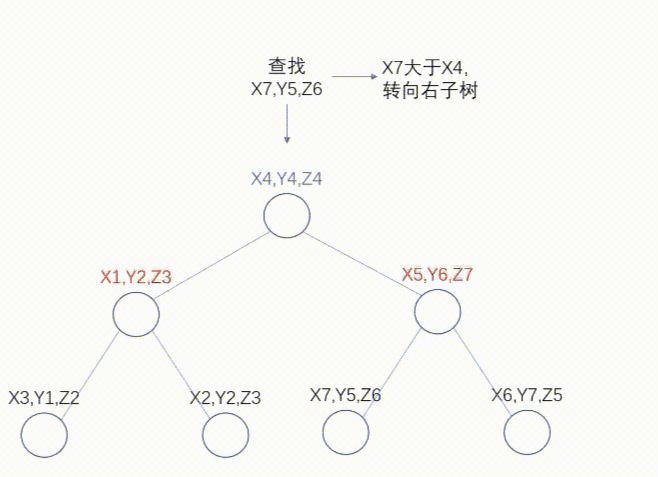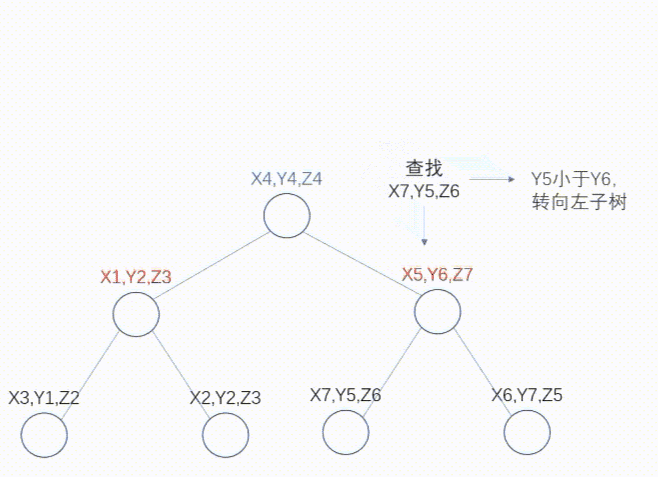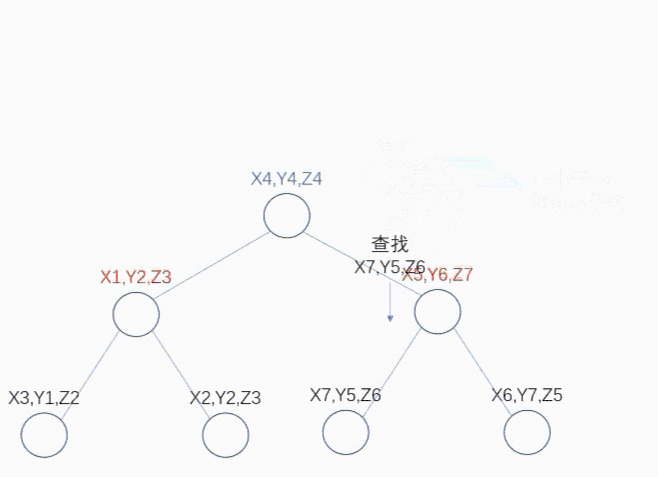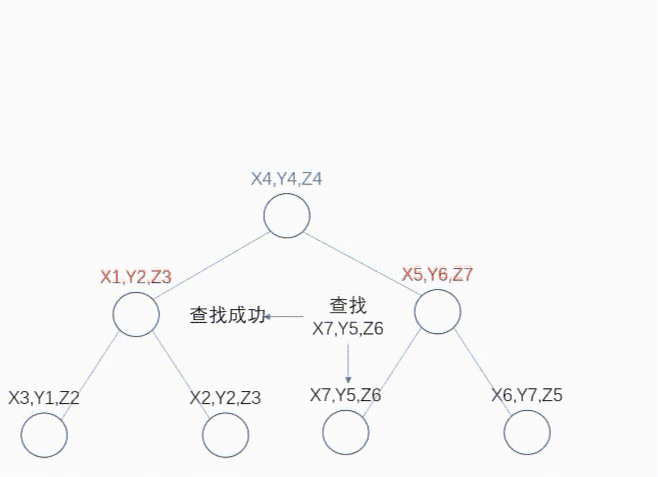
添加
添加的的逻辑也是相当直观,就像查找一样,这里就不多说了。
删除
无论是一维的二叉查找树还是kd二叉查找树,删除逻辑都是比较复杂的。一维二叉查找树删除看这里数据结构与算法-二叉查找树。类比一维二叉查找树的删除,从最直观的角度出发,我们将kd树删除分成3种情况来考察。
1、删除叶子节点
毫无疑问,删除叶子节点直接释放叶子节点空间即可,因为叶子节点没有子树需要处理,所以直接删除。
2、删除度为1的节点
在一维二叉查找树中,删除度为1的节点也是比较简单的,直接将唯一的子树提升到被删除节点层次即可。但是在kd树中,这样处理是不行的。因为被删除节点以及子树处于不同的层次,提升子树到被删除节点的层次是不可行的。假如现在有被删除节点P,子树根节点为Q,Q存在子节点R,其中,P层比较x值,Q层比较y值,如果节点Q是节点P的左节点,那么x(Q)<x(P),节点R是节点Q的左节点,那么y(R)<y(Q)。假设删除P之后,提升Q节点到P原有的位置,需要保证x(R)<x(Q),但是我们只能保证y(R)<y(Q),所以直接提升子树的层次是不可行的。
3、删除度为2的节点
类比一维二叉查找树中度为2节点的删除逻辑,无非是合并删除或者复制删除,其中合并删除明显是不可行的,原因也是子树合并之后依然要提升子树到被删除节点的层次,这是不可行的。复制删除可以吗?假设被删除节点为P,左子树为Q,右子树为R。复制删除的核心逻辑是在Q中找到最大的节点替换P或者在R中找到最小的节点替换P。本质是,能够替换P的节点要大于Q中任意节点,小于R中任意节点。将其扩展到kd二叉查找树,什么样的节点可以替换被删除节点呢?
假设被删除节点为P,我们将以P节点为根的子树截取出来,问题就转化为如何删除kd二叉查找树的根节点。当前的难点在于找到一个什么样的节点来替换根节点,这就需要观察根节点的特性了。还记得插入节点的逻辑吗?假设插入新节点Q,首先将Q节点的x维度的值和根节点x维度的值比较,大于则转向右子树,小于则转向左子树,在此过程中,其他维度的值不起作用。也就是说,根节点的x维度的值大于左子树中任意节点的x维度的值,小于右子树中任意节点的x维度的值,其他维度的值大小没有要求。那么答案就显而易见了,能够替换根节点的只有两个,首先是左子树中x维度值最大的节点,其次是右子树中x维度值最小的节点。怎么找呢?没什么好的办法,因为这两个可替换节点的位置没有固定的规律,只能遍历所有节点来寻找。就算找到了,如果该节点也是度为2的节点,那么删除它的逻辑和上面是一样的,依然要遍历寻找可替换的节点,直到找到叶子节点,才可以直接删除。
删除度为1的节点和删除度为2的节点逻辑是一样的,找到可替换节点才行。
伪代码如下:
假设q节点是被删除节点右子树的根节点,下面是查找q子树中i维度值最小节点的逻辑
smallest(q, i) {
min = q;
if q->left != 0
lt = smallest(q->left, i);
if min->el.keys[i] >= lt->el.keys[i]
min = lt;
if q->right != 0
rt = smallest(q->right, i);
if min->el.keys[i] >= rt->el.keys[i]
min = rt;
return min;
}伪代码的逻辑是使用递归,逐个比较每个节点的x维度值的大小。显然,这种方式不够优秀,我们还可以继续改进。改进点在于,如果我们知道某节点R是比较x维度的值,那我们就不用遍历R节点的右子树了,因为R节点的左子树任意节点的x维度的值小于R节点x维度的值,而R节点x维度的值是小于R节点右子树任意节点x维度值的。所以,如果我们检测到当前比较节点比较的是x维度的值,直接选择它的左子树即可。
伪代码如下:
假设q节点是被删除节点右子树的根节点,下面是查找q子树中i维度值最小节点的逻辑
smallest(q, i, j) {
min = q;
if i == j
if q->left != 0
min = q = q->left;
j = j + 1
else
return q;
if q->left != 0
lt = smallest(q->left, i, (j + 1) mode k);
if min->el.keys[i] >= lt->el.keys[i]
min = lt;
if q->right != 0
rt = smallest(q->right, i, (j + 1) mode k);
if min->el.keys[i] >= rt->el.keys[i]
min = rt;
return min;
}到此为止,我们已经介绍了kd二叉查找树的创建、查找、添加、删除算法。但是我们依然有很多困惑没有解决,比如说添加或者删除会破坏kd树的平衡,怎么处理?删除算法复杂且效率不高,怎么改进?kd二叉查找树有哪些应用?等等,这些问题在下一篇文章进行探讨。

 随时随地看视频
随时随地看视频




