时间序列 - 识别方波型信号的方法

Question

我正在尝试寻找一种方法来过滤掉具有如下所示模式的信号。

该模式可以描述为具有方波，通常在多个时间段内具有恒定的波动值+-1、+-2 或+-0。信号通常会瞬间下降到 5-100 标准差，然后在很短的时间内保持恒定速率，然后再次回升。这些类型的信号可以具有单个或多个不同长度的方波，但信号中始终呈现方波。

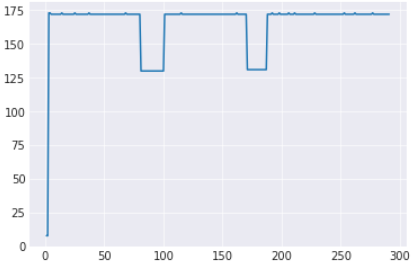
我需要找到一种方法，可以帮助我从大约 3000 个信号中聚类出或过滤掉这些信号。我尝试了以下方法并得到了非常复杂的结果：

• 使用 TSLearn 和 DTW python 包对数字方差相关特征进行单变量时间序列聚类（混合结果）

• 使用 K-Means、KNN 等进行多元聚类（通常可以为单个信号分配多个聚类。规则是一个信号对应一个桶，而不是多个桶）

• 在数组中查找子序列的条件逻辑，希望找到方波（我对此无能为力，因为良好信号的一半长度可以等于信号重要部分的长度的一半；方波）

• 核分布估计（我有其他信号与该信号具有相同的分布，因此我无法根据系数的排名/聚类过滤掉这些信号）

您能否推荐其他方法来帮助我从一组其他信号中识别此类信号？如果您的方法是傅里叶变换，您能否提供一个示例，说明我如何使用它从一组其他信号中过滤掉该信号？

Answer 1

这将做到这一点：def first_der(df):&nbsp; y = df.NREVS.values&nbsp; x = df.cum_int.values&nbsp; dy=np.diff(y,1)&nbsp; dx=np.diff(x,1)&nbsp; yfirst=dy/dx&nbsp; return yfirstdef zero_runs(yfirst):&nbsp; &nbsp; # Create an array that is 1 where a is 0, and pad each end with an extra 0.&nbsp; &nbsp; iszero = np.concatenate(([0], np.equal(a, 0).view(np.int8), [0]))&nbsp; &nbsp; absdiff = np.abs(np.diff(iszero))&nbsp; &nbsp; # Runs start and end where absdiff is 1.&nbsp; &nbsp; ranges = np.where(absdiff == 1)[0].reshape(-1,2)&nbsp; &nbsp; return yind&nbsp;&nbsp;def square_finder(yfirst, yind, df):&nbsp; xmax = yind.shape[0]&nbsp; #max value in first position where y_first can be indexed&nbsp; ymax = yind.shape[1] #max value in second position&nbsp; thresh = 4&nbsp; for i in range(0,xmax):&nbsp; &nbsp; if yind[i][1] < len(yfirst):&nbsp; &nbsp; &nbsp; if ((yfirst[yind[i][1]] > 5) | (yfirst[yind[i][1]] < -5)):&nbsp; &nbsp; &nbsp; &nbsp; #if ((yfirst[yind[i-1][1]+1] > 3) | (yfirst[yind[i-1][1]+1] < -3)):&nbsp; &nbsp; &nbsp; &nbsp; zeros = yind[i][1] - yind[i-1][1] - 2&nbsp; &nbsp; &nbsp; &nbsp; if zeros >= thresh:&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; df['category'] = 'square'&nbsp; &nbsp; &nbsp; &nbsp; else:&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; pass&nbsp; &nbsp; &nbsp; else:&nbsp; &nbsp; &nbsp; &nbsp; pass&nbsp; &nbsp; else:&nbsp; &nbsp; &nbsp; pass&nbsp; return df