Sympy 乘以答案改变它并使其错误

Question

我试图找到矩阵的逆矩阵，但是 sympy 总是将最终答案乘以 4，从而使答案错误。当我使用因子函数时，也会发生这种乘法。

这是我要更改的矩阵

import sympy as sy

z = sy.symbols('z')

t = sy.Matrix([[z, -1], [sy.Rational(1,4), z + 1]])

t.inv()

这是它给出的“错误”答案 

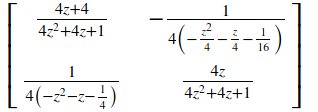
真正的答案是相同的，只是不乘以 4。为什么 sympy 会这样相乘答案呢？

为了隔离问题，我们可以尝试分解行列式。

如果我们分解行列式，我期望答案为(z+1/2)**2 但这是我得到的答案，它除以 4 和 ，乘以 2。期望的答案必须恰好是 (z+ 1/2)^2 不是乘法版本 sympy 输出。

d = t.det()

print("I want to factor this")

display(d)

print("After factoring")

display(sy.factor(d))

print(" \n The right answer I was expecting")

display((z+sy.Rational(1,2))**2)

我正在解决的问题是 Z 变换的演变，而因子的乘法导致最终答案错误。因子或极点必须准确无误，无需任何乘法，即答案必须准确为 (z+1/2)^2

有没有办法让 sympy 给我确切的因素？

Answer 1

小心你的措辞：你得到的答案没有任何“错误”。您希望以不同的形式得到答案，这很好，但给出的答案是正确的。如果您考虑高斯有理数，您可以得到您想要的形式：In [41]: e = z**2 + z + Rational(1, 4)                                                                                                         In [42]: e                                                                                                                                     Out[42]:  2       1z  + z + ─         4In [43]: factor(e)                                                                                                                             Out[43]:          2(2⋅z + 1) ──────────    4     In [44]: factor(e, gaussian=True)                                                                                                                Out[44]:          2(z + 1/2) In [45]: t.inv()                                                                                                                               Out[45]: ⎡    4⋅z + 4              -1        ⎤⎢ ──────────────   ─────────────────⎥⎢    2               ⎛   2         ⎞⎥⎢ 4⋅z  + 4⋅z + 1     ⎜  z    z   1 ⎟⎥⎢                  4⋅⎜- ── - ─ - ──⎟⎥⎢                    ⎝  4    4   16⎠⎥⎢                                   ⎥⎢       1                4⋅z        ⎥⎢────────────────   ──────────────  ⎥⎢  ⎛   2       1⎞      2            ⎥⎢4⋅⎜- z  - z - ─⎟   4⋅z  + 4⋅z + 1  ⎥⎣  ⎝           4⎠                   ⎦In [46]: t.inv().applyfunc(lambda e: factor(e, gaussian=True))                                                                                   Out[46]: ⎡   z + 1          1     ⎤⎢ ──────────   ──────────⎥⎢          2            2⎥⎢ (z + 1/2)    (z + 1/2) ⎥⎢                        ⎥⎢    -1            z     ⎥⎢────────────  ──────────⎥⎢           2           2⎥⎣4⋅(z + 1/2)   (z + 1/2) ⎦