具有两种背包尺寸的多维成本 0-1 背包问题
我正在研究在leetcode上找到的这个问题的解决方案。
问题指出:
给定一个数组 ,其字符串仅由0和1
strs组成。还有两个整数和。mn
m现在你的任务是找到给定的0 和n1可以组成的最大字符串数。每个0和1最多只能使用一次。
输入:
strs = ["10","0001","111001","1","0"],m = 5,n = 3输出:
4
解释:用5个0和3个1可以组成4个字符串,分别是“10”、“0001”、“1”、“0”。
用于解决该问题的算法如下:
def findMaxForm(strs, m, n):
dp = [[0] * (n + 1) for _ in range(m +1)]
for s in strs:
zeros, ones = s.count('0'), s.count('1')
for i in range(m, zeros - 1, -1):
for j in range(n, ones -1, - 1):
# dp[i][j] indicates it has i zeros ans j ones,
# can this string be formed with those ?
dp[i][j] = max( 1 + dp[i - zeros][j - ones], dp[i][j])
# print(dp)
return dp[-1][-1]
问题的混乱部分是dp[i][j] = max( 1 + dp[i - zeros][j - ones], dp[i][j]). 我不确定这里发生了什么。为什么我们从 0 中减去 i,从 1 中减去 j?
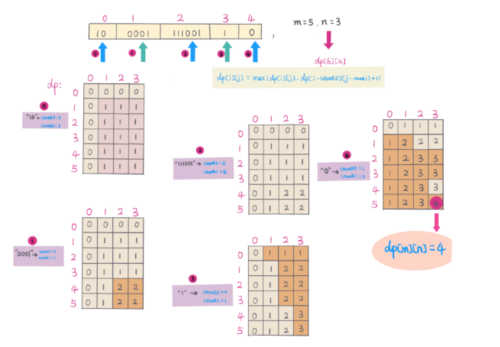
我还找到了一张图表,解释了 dp 表应该如何查找数组中的所有元素。
我的问题:
第一张表代表什么?x 和 y 轴?为什么有这么多
1的。我想如果我理解了这一部分,可能会有所作为。如果有人浏览图表,我将不胜感激为什么这种方式给了我们可以形成的最大数量的
0'和1'?我想我对这部分仍然感到困惑dp[i][j] = max( 1 + dp[i - zeros][j - ones], dp[i][j])。该解决方案还被描述为“针对 2D 空间优化的 3d-DP:dp[j][k]:i 维度经过优化以就地使用。” 这意味着什么?
 LEATH
LEATH1回答
-

HUWWW
遇到字符串时s,基本上有两种选择。它要么属于最大解,要么不属于。如果这样做,集合的大小会增加 1,但剩下的 1 和 0 会减少。如果您不使用它,集合的大小将保持不变,但如果保留 1 和 0,则数字也会保持不变。该表dp代表了到目前为止您可以获得的最大此类集合,用于“左”的不同数量的 1 和 0。例如。dp[m][n]表示到目前为止您可以使用m0 和n1 获得的最佳值。同样,对于dp[2][3]其余字符串,您可以使用 2 个零和 3 个一。让我们把它包装在一起:对于一些给定数量的零 ( i) 留下来使用,一些零 ( j) 留下来使用,以及一个字符串s:1 + dp[i - zeros][j - ones]表示如果您决定添加到集合中的最大集合s(并且您只剩下更少的 1 和 0)dp[i][j]意味着你没有接受这个元素,继续前进。当您调用max()这两个值时,您基本上是在说:我想要这两个选项中更好的一个。我希望这能回答前两个问题,即为什么它是最大的以及 dp 线的含义。该解决方案还被描述为“针对 2D 空间优化的 3d-DP:dp[j][k]:i 维度经过优化以就地使用。” 这意味着什么?在这里,你有 3d 问题:你迭代的字符串本身 - 但你没有数组的另一个维度。您将其优化为就地,因为您始终只需要前一个字符串,而不需要比它“更旧”的字符串,从而节省了宝贵的空间。
 随时随地看视频慕课网APP
随时随地看视频慕课网APP
相关分类

 Python
Python