参考线与折线的连续点之间的正交距离

Question

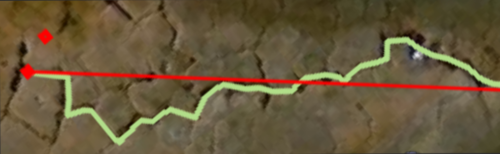
该图像显示 (1) 一条我称之为参考线的红线，以及 (2) 一条黄色多段线。每个线要素由数千个 x,y 坐标对点组成。我想沿着红色参考线逐步移动，并计算到黄色折线的每个坐标对点的正交距离（相对于红线）。我在 python 3中工作。

以下是红色参考线的前 25 个坐标对：

以下是黄色折线的前 25 个坐标对：

我一直在尝试一些基于here、here和here的方法。我正在测试在最后一个超链接中讨论的答案以尝试构建工作流程：

import numpy as np

from shapely.geometry import LineString, Point

x1 = 457508.40746964136

x2 = 457508.5456318401

y1 = 8872649.617776532

y2 = 8872649.773129418

dist = np.sqrt((x2 - x1)**2 + (y2 - y1)**2)

centerX = (x2 - x1) / 2 + x1

centerY = (y2 - y1) / 2 + y1

test_x = centerX - dist/4

test_y = centerY + dist

line = LineString([(x1, y1), (x2, y2)])  

print(list(line.coords))

p = Point(test_x,test_y)  

print(list(p.coords))

print(p.distance(line))

p.distance(line) 返回：0.17780 ...这是此特定测试的图像：

黑点是红色参考线上的两个连续坐标对。红点是测试坐标对，用于计算黑点到淡蓝色线段的正交距离。在我看来，上面给出的 p.distance 结果对于正交距离来说太短了。如果能帮助我在这个问题上取得进展，我将不胜感激。提前致谢。

Answer 1

从点(test_x,test_y)到线的正交距离(x1,y1)-(x2,y2)可以用向量代数计算orthodistance = abs((y2 - y1)*test_x - (x2 - x1)*test_y + x2*y1 - y2*x1) / dist)这个表达式给出了0.176你的数据，所以结果看起来很接近。请注意，您的图像比例并不完美 - 图在 X 方向上被拉伸，这就是您可能会怀疑的原因。