将记忆化应用于硬币更换问题

Question

我正在尝试解决以下问题（来自CodeRust 3.0）：

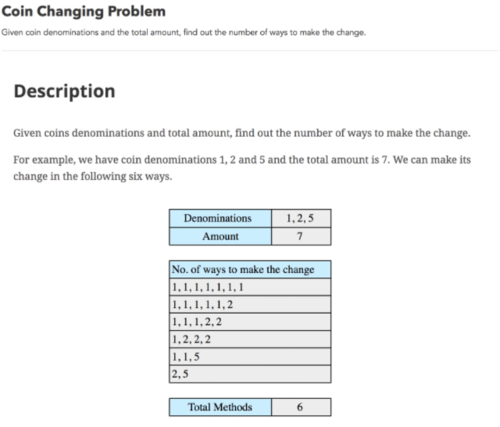
我想我会利用以下递归关系：在这个例子中，用面额制作 7(1, 2, 5)的方法数是0, 1, ..., 7用面额制作的方法数的总和(2, 5)（即，对较小的一组的递归调用第一枚硬币数量的每个选择的面额，1）。

为了应用记忆，我想我会使用functools.lru_cache(). 到目前为止，这是我的解决方案（包括pytest单元测试）：

import pytest

import functools

@functools.lru_cache()

def solve_coin_change_dp(denominations, amount):

    if amount == 0:

        return 1

    if amount < 0:

        return 0

    if not denominations:

        return 0

    return sum(

        solve_coin_change_dp(

            denominations[1:],

            amount - i * denominations[0])

        for i in range(amount // denominations[0] + 1))

@pytest.fixture

def denominations():

    return (1, 2, 5)

def test_trivial():

    assert solve_coin_change_dp((1,), 1) == 1

def test_1(denominations):

    assert solve_coin_change_dp(denominations, 1) == 1

def test_2(denominations):

    assert solve_coin_change_dp(denominations, 2) == 2

def test_3(denominations):

    assert solve_coin_change_dp(denominations, 3) == 2

def test_4(denominations):

    assert solve_coin_change_dp(denominations, 4) == 3

def test_5(denominations):

    assert solve_coin_change_dp(denominations, 5) == 4

def test_7(denominations):

    assert solve_coin_change_dp(denominations, 7) == 6

def test_big_amount(denominations):

    solve_coin_change_dp(denominations, 1000)

if __name__ == "__main__":

    pytest.main([__file__, '--duration', '1'])