关于红包总金额问题
来源:6-9 红包算法-先洗牌算法设计和编程实践

misaki_rain
2019-03-07 16:48
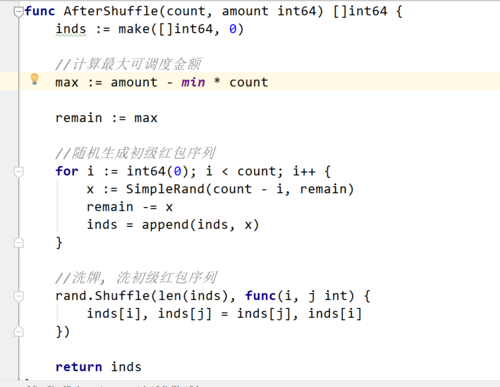
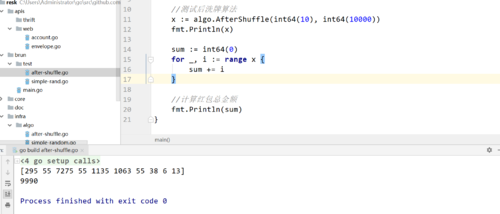
后洗牌算法产生的红包序列总额( 9990 )跟发红包的总金额(10000)不一致 , 是因为在计算最大可调度金额时减去 min * count , 导致红包金额总小于总金额 有没有大神解释一下这是为什么?
写回答
关注
3回答
-

- 枫荇
- 2019-03-07 21:43:28
@misaki_rain 很认真的一位同学,实际上通过这个bug,也可以更深刻的理解最小金额的意义。除了生成序列还进一步对生成的结果做了一些验证,这些思考和验证方法可以进一步使用自动化测试来验证,实际上后洗牌算法在课程中没有编写自动化测试来验证,没有测试就有bug,也说了测试的重要性。非常感谢@misaki_rain的问题,非常棒!???
-

- 慕婉清5328337
- 2019-04-19 12:17:54
func AfterShuffle(count,amount int64) []int64 { var ( inds []int64 remain int64 ) //计算最大可调度金额 //max := amount-min*count remain = amount for i:=int64(0);i<count;i++{ x := SimpleRand(count-i,remain) remain -=x inds = append(inds,x) } .... 总结以上盆友,已在"简单随机算法SimpleRand"计算了最大可调度金额,故:此处再计算max,已属画蛇添足了; -

- misaki_rain
- 2019-03-07 17:44:17
在aftershuffle中 inds = append(inds, x)应该改为inds = append(inds, x + min) 总金额就一样的了 图中代码一个bug 打扰了
3小时极简春节抢红包之Go的实战
【毕业设计】春节抢红包业务资金交易秒杀系统的架构设计和Golang实战
12271 学习 · 32 问题
相似问题

