-

- Mrsls 2019-07-25
大型神经网络
-
截图0赞 · 0采集
-

- Mrsls 2019-07-25
加入矩阵维度
-
截图0赞 · 1采集
-

- Mrsls 2019-07-25
输入->隐含->输出->结果值
-
截图0赞 · 0采集
-

- R6S猿 2018-11-25
大型神经网络结构概念式
-
截图0赞 · 0采集
-

- R6S猿 2018-11-25
向量化之后的最后表达式
-
截图0赞 · 0采集
-

- R6S猿 2018-11-25
网格向量化具体过程
-
截图0赞 · 0采集
-

- R6S猿 2018-11-25
W、B要把X转变为a这中维度
-
截图0赞 · 0采集
-

- R6S猿 2018-11-25
网络向量化
-
截图0赞 · 0采集
-

- 李爱菊 2018-10-06
为了反向调整w、b的值,修改正向传播的计算公式:
-
截图0赞 · 0采集
-

- 李爱菊 2018-10-06
z = wT*x+b
输入几个x,w的第一纬就是几;比如这里有3个x,则w就是3行;
该层有几个细胞,w的第二维就是几;比如这里隐含层有4个细胞,则w就是4列。
然后,w转置后,与x相乘;
该层有几个细胞,b的第一维就是几;这里b是4行1列。
输出层,也是,一个细胞,四个输入;则w是4行1列,b是1行1列。
-
截图0赞 · 0采集
-

- 明天也爱你 2018-07-21
神经网络的网络向量化
神经网络的向前传播、运算、预测——神经网络的网络向量化,对向量化进行计算的过程


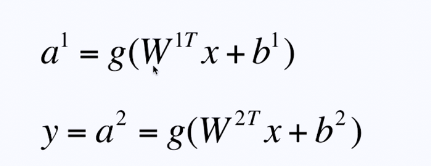

- 0赞 · 0采集
-

- 慕先生0302488 2018-06-01
x = a ^n-1
-
截图0赞 · 0采集
-

- 慕先生0302488 2018-06-01
結果顯示:
-
截图0赞 · 0采集
-

- 慕先生0302488 2018-06-01
逻辑回归关系(线性组合W与b、激活函数g)
-
截图0赞 · 0采集
-

- 慕先生0302488 2018-06-01
向點結果a
-
截图0赞 · 0采集
-

- 顺反异构小宇宙 2018-05-12
对各层而言处理W和b的自身格式不同,其处理过程相似都可以归纳为
注:这里的x可以为输入,也可以为上一层的输出a n-1
-
截图0赞 · 0采集
-

- 顺反异构小宇宙 2018-05-12
可以将上述过程总结为
-
截图0赞 · 0采集
-

- 顺反异构小宇宙 2018-05-12
各层之间都存在的逻辑回归关系(线性组合W与b、激活函数g),各层间的W和b需满足一定格式来实现矩阵维度的变化,如截图所示
-
截图0赞 · 0采集
-

- 顺反异构小宇宙 2018-05-12
网络向量化:
也叫 神经网络向前传播/神经网络的预测
对于一个单隐藏层神经网络(如图1),其各层的输入输出可以表示为(见截图),x1、x2、x3表示输入层的输入,a11~a41表示隐藏层的4个输出,a2表示输出层的输出
-
截图0赞 · 0采集
-

- Mr天旭 2018-05-11
就是神经网络图形化设计转化为向量表示的公式化
- 1赞 · 0采集
-

- Ian_Morris 2018-03-25
网络向量化推广的表达式
-
截图0赞 · 0采集
-

- Ian_Morris 2018-03-25
网络向量化=神经网络向前传播=神经网络的预测
-
截图0赞 · 0采集
-

- 发奋的大西瓜霜 2018-03-01
- 网络向量化
-
截图0赞 · 0采集
-

- 霜花似雪 2017-12-25
- 网络向量化公式
-
截图0赞 · 2采集
-

- 霜花似雪 2017-12-25
- 网络向量化
-
截图0赞 · 1采集
数据加载中...









