deepth

broadf

doing edge

prim算法是：假设从顶点A开始， 先选距离A最近的顶点（比如F），然后把把F点放入已涉及顶点集合当中，A-F边放入已选边的集合中。之后将A和F看作一个整体，再去找理这个整体最近的点和边。

kruskal算法是：先把所有的边找到，每一次都去找所有边中最短的那一条。不断的把顶点连接起来，直到所有的顶点都放入顶点集合中 并且通过边形成同一个集合为止。

2种算法都要在选边的过程中不断判断选择的边是否会和已有边形成闭环，如果形成闭环就要舍弃

Prim算法：

选了F点后：

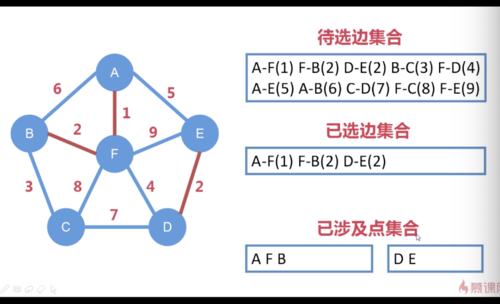
Kruskal算法：（最先选最小的边，再选次笑的边，前提是选边后不要造成闭环）

因为选的边没有交集，所以点集合分为两个集合

图的遍历：深度搜索（前序遍历）和广度搜索

深度搜索（前序遍历）：

广度搜索（较好理解，一层一层地搜索）

不同的搜索方式得到的生成树不同，上述较为简单，未涉及到权的问题。

若有权：最小生成树

两种算法：Prim算法 & Kruskal算法

最小生成树：1.所有的店都必须在一个集合中

2.中间不能形成闭合通路

3.关系值最优

克鲁斯卡尔算法：

    待选边集合，已选边集合，已涉及点集合

    从待选边中选一条权最小的边，将该边加入已选边集合，将这条边连接的两个点加入到已涉及点集合；然后再从待选边中选一条去掉已选边集合中的边的权值最小的边，（判断改边是否会让已选边集合构成圈），如果不构成边则将该边加入到已选边集合中，并将涉及的点加入到已涉及点集合中，依此类题~

普里姆算法：

    一个顶点集，一个边集，一个待选边集

    从某个点开始，这个点连接的所有边加入待选边集合，选择权最小的一条边加入到边集，将这条变连接的另一个点加入到顶点集，然后将这个点连接的所有边加入到待选边集合，以此类推...  每选择一条边的时候需要判断当前边的加入是否形成环。

最小生成树算法：

【图的遍历】深度优先搜索（前序遍历）、广度优先搜索（一层一层搜索）

【最小生成树】普里姆Prim算法、克鲁斯卡尔Kruskal算法

1、Prim算法

• 点集合

• 边集合

• 待选边集合

2、Kruskal算法

• 待选边集合

• 已选边集合

• 已涉及点集合