-

- 单挑谁怕谁 2025-12-21
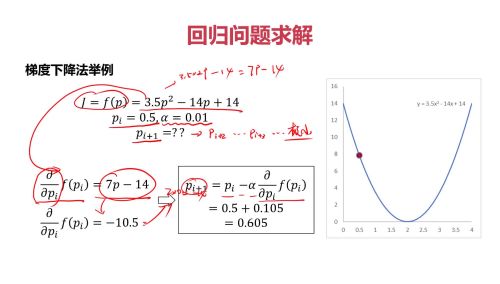
梯度下降法

- 0赞 · 0采集
-

- Keyro 2025-08-24
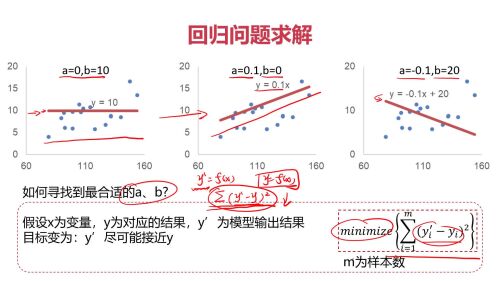 回归问题求解
回归问题求解- 0赞 · 0采集
-

- Keyro 2025-08-24
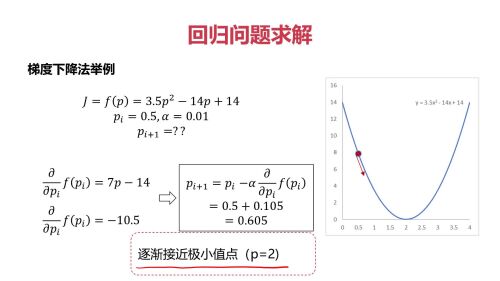 回归问题求解
回归问题求解- 0赞 · 0采集
-

- Keyro 2025-08-24
 梯度下降法
梯度下降法- 0赞 · 0采集
-

- 崔华乐 2024-04-16
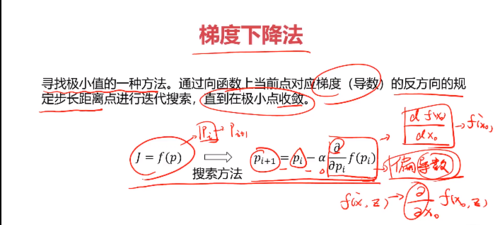
一、梯度下降法 (梯度即导数)
寻找极小值的一种方法。通过向函数上当前点对应梯度(导数)的反方向的规定步长距离点进行迭代搜索,直到在极小点收敛。
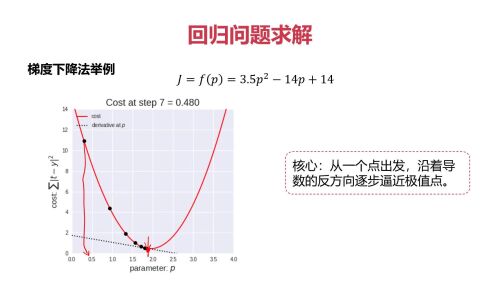
核心:从一个点出发,沿着导数的反方向逐步逼近极值点。
- 0赞 · 0采集
-

- 慕少7339756 2023-11-23
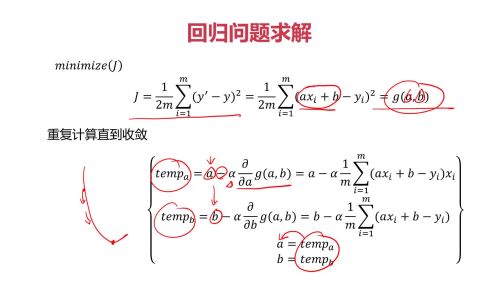
梯度下降法:

梯度下降举例:求极小值点
例子2:回归问题
例子2:回归问题:如何找合适a,b?方差(损失函数)最小
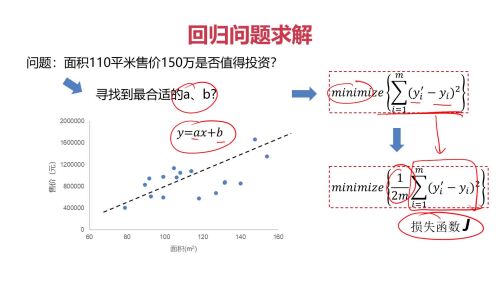
例子2:回归问题:如何找下一个点
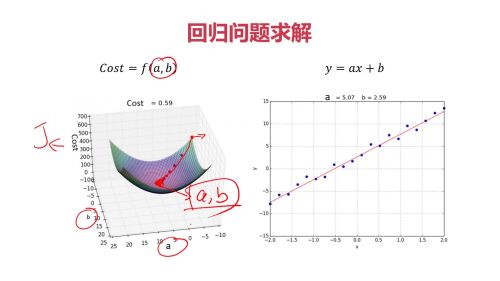
例子2:回归问题:求解效果
- 0赞 · 0采集
-

- 洲帅 2023-05-18
 梯度下降法
梯度下降法- 0赞 · 0采集
-

- 莱旺多夫斯基 2022-04-01
梯度下降法

梯度下降法举例
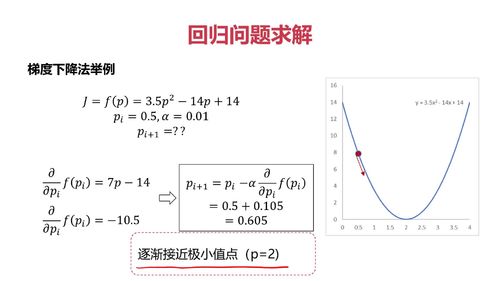
核心:从一个点出发,沿着导数的反方向逐步逼近极值点
回归问题求解



- 0赞 · 0采集
-

- 慕桂英7589197 2021-10-05


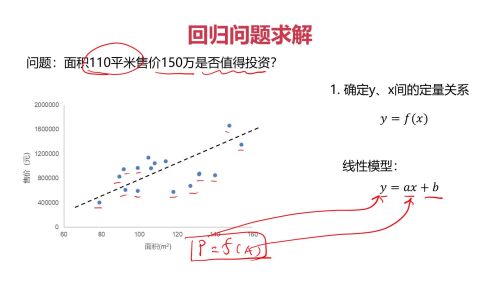
回归问题求解:
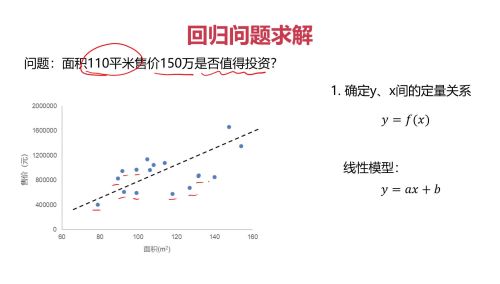
建立模型得到面积和房价的关系
先假设存在一个线性关系,y=ax+b,查找合理的a和b的过程

通过人眼来看,如何计算机寻找合适的a和b的核心思路。
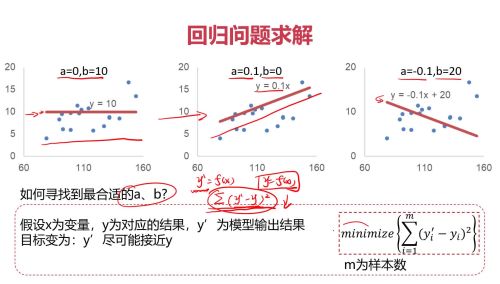
距离的平方之和最小。
梯度下降法,能够找到极值点

能实现上面最小的时候,下面的式子也是最小的。

慢慢寻找极小值对应的a和b的值。

- 0赞 · 0采集
-

- 亦是随心 2020-11-28
梯度下降法

-
截图0赞 · 0采集
-

- 1561147120 2020-08-28
模型求解(AI相关的模型)与梯度下降法

偏导数,用于两个或以上的自变量的情况
寻找适合的a 和 b 值
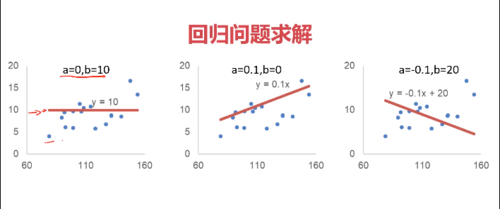
目标:尽可能使模型模拟出来的y值接近实际的y值,使两者差值的平方最小化

引入损失函数,使导数后的平方抵消,由于存在m个样品,也除以m
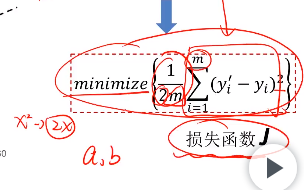
应用梯度下降法来计算收敛

最后获得一条最优解
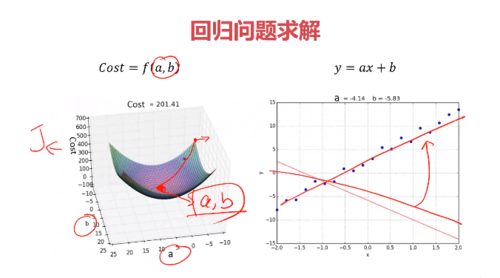
- 1赞 · 2采集
数据加载中...

















