-

- Keyro 2025-08-25
 混淆矩阵
混淆矩阵- 0赞 · 0采集
-

- Keyro 2025-08-25
 使用准确率进行模型评估的局限性
使用准确率进行模型评估的局限性- 0赞 · 0采集
-

- Keyro 2025-08-25
 逻辑回归模型
逻辑回归模型- 0赞 · 0采集
-

- 扶云归 2024-09-10

1
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26

混淆矩阵指标的特点和选择指标的介绍
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26
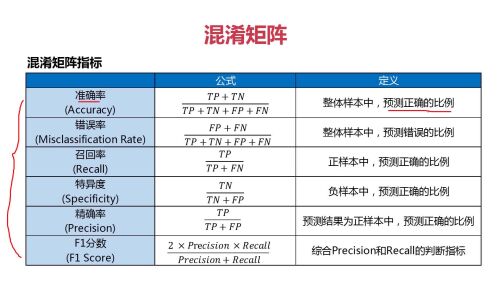
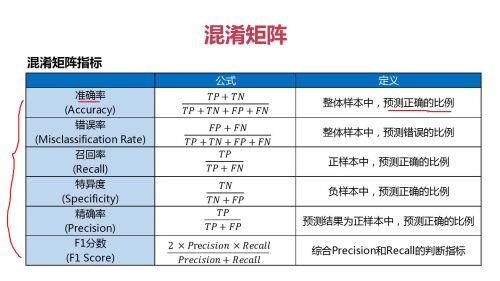
混淆矩阵的主要指标
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26
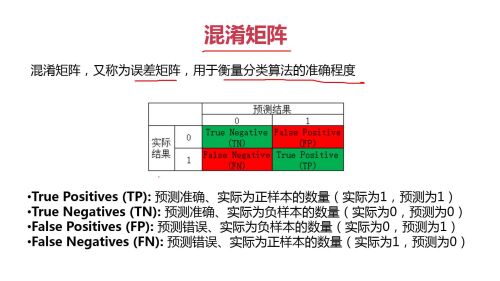
介绍了混淆矩阵的作用
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26
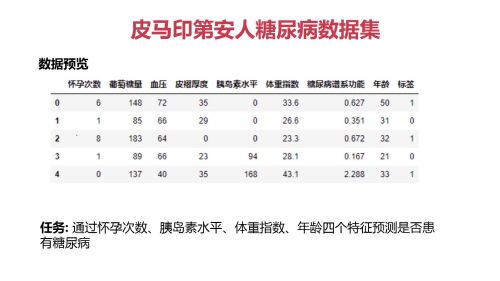
介绍任务
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26

数据集大致介绍
- 0赞 · 0采集
-

- 慕斯卡6411321 2023-11-26
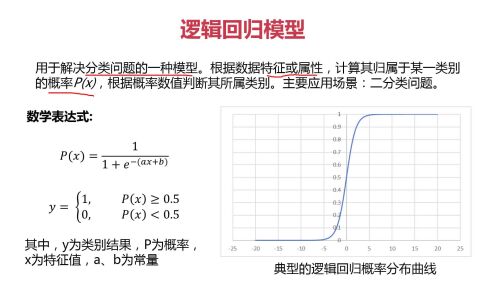
这是回归模型的数学表达式及模型展示
- 0赞 · 0采集
-

- 洲帅 2023-05-11
 2
2- 0赞 · 0采集
-

- 洲帅 2023-05-11
 1
1- 0赞 · 0采集
-

- 慕婉清7089129 2021-11-30
使用准确率模型评估,有很大的局限性(无法真实反映内部实际分布情况)
混淆矩阵
垃圾邮件识别
1)准确率
2)召回率
- 0赞 · 0采集
-

- shuidiyoushu 2020-12-23
 混淆矩阵的指标
混淆矩阵的指标- 0赞 · 0采集
-

- qq_钻石星泪_0 2020-10-02
使用准确率进行模型评估的局限性

- 0赞 · 1采集
-

- 小小程序员一枚 2020-07-14
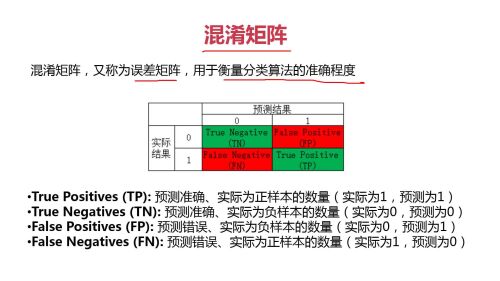
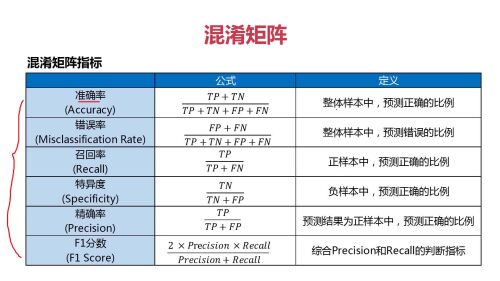
# True Positives(TP):预测准确、实际为正样本的数量(实际为1,预测为1) # True Negatives(TN):预测准确、实际为负样本的数量(实际为0,预测为0) # False Positives(FP):预则错误、实际为负样本的数量(实际为0,预测为1) # False Negatives(FN):预测错误、实际为正样本的数量(实际为1,预测为0) # 准确率 (TP+TN)/(TP+TN+FP+FN) 整体样本中,预测正确的比例 # 错误率 (FP+FN)/(TP+TN+FP+FN) 整体样本中,预测错误的比例 # 召回率 TP/(TP+FN) 正样本中,预测正确的比例 # 特异度 TN/(TN+FP) 负样本中,预测正确的比例 # 精确率 TP/(TP+FP) 预测结果为正样本中,预测正确的比例 # F1分数 2*精确率*召回率/(精确率+召回率) 综合精确率和召回率的指标
-
截图0赞 · 1采集
-

- 小小程序员一枚 2020-07-14
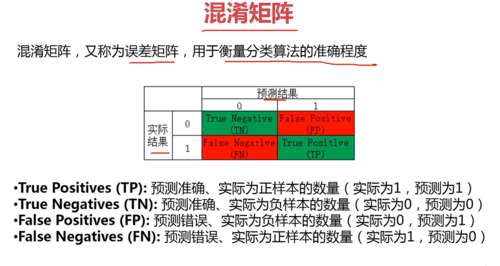
# 泥淆矩阵,又称为误差矩阵,用于衡量分类算法的准确程度 # --------------------预测结果--------------------------------- # 0 1 # 实际 0 True Negatives(TN) False Positives(FP) # 结果 1 False Negatives(FN) True Positives(TP) # ------------------------------------------------------------ # True Positives(TP):预测准确、实际为正样本的数量(实际为1,预测为1) # True Negatives(TN):预测准确、实际为负样本的数量(实际为0,预测为0) # False Positives(FP):预则错误、实际为负样本的数量(实际为0,预测为1) # False Negatives(FN):预测错误、实际为正样本的数量(实际为1,预测为0)
- 0赞 · 0采集
-

- Lady_Eva14 2020-07-13
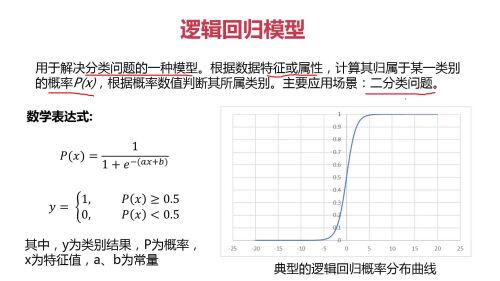
逻辑回归:计算概率判断类别,应用场景 二分类问题
准确率预测的局限性:准确度存在空准确率的问题(直接丢掉了负样本,只关注正样本)、没有体现实际分布情况、没有体现模型错误预测类型
混淆矩阵:又称为误差矩阵,衡量分类算法的准确程度,含6个指标
- 0赞 · 0采集
-

- weixin_慕慕249459 2020-03-25
准确率 (TP+TN)/(TP+TN+FP+FN)
错误率 (FP+FN)/(TP+TN+FP+FN)
召回率 TP/(TP+FN)
特异度 TN/(TN+FP)
精确率 TP/(TP+FP)
F1分数 2*精确率*召回率/(精确率+召回率)
-
截图0赞 · 0采集
-

- weixin_慕慕249459 2020-03-25
混淆矩阵,用于衡量分类算法的准确程度
True Positives(TP):预测准确、实际为正样本的数量(实际为1,预测为1)
True Negatives(TN):预测准确,实际为负样本的数量(实际为0,预测为0)
False Positive(FP):预测错误、实际为负样本的数量(实际为0,预测为1)
FalseNegatives(FN):预测错误、实际为正样本的数量(实际为1,预测为0)
-
截图0赞 · 0采集
-

- weixin_慕慕249459 2020-03-24
逻辑回归模型:计算数据归属于某一类别的概率P,根据概率数值判断其类别。主要应用于二分类问题
-
截图0赞 · 1采集
-

- weixin_慕慕249459 2020-03-24
逻辑回归模型:在二分类问题中使用更加广泛
使用准确率进行模型评估的局限性
混淆矩阵、模型衡量指标及其意义
-
截图0赞 · 1采集
-

- jingleYao 2020-02-16
匹马印第安人数据集
数据来源:
Pima Indians Diabetes dataset
-
截图0赞 · 1采集
-

- jingleYao 2020-02-15
混淆矩阵的应用举例
-
截图1赞 · 1采集
-

- jingleYao 2020-02-15
混淆矩阵的指标
-
截图1赞 · 1采集
-

- jingleYao 2020-02-15
混淆矩阵的定义
-
截图1赞 · 1采集
-

- jingleYao 2020-02-15
使用准确率进行模型评估的局限性
不能体系那数据的实际分布情况
没有体现模型错误预测的类型
空准确率的概念
-
截图0赞 · 1采集
-

- jingleYao 2020-02-15
逻辑回归模型
准确率进行模型评估有其局限性,只能看到整体,而不知细节。
比如1000个数据(900个1,100个0),全部预测为1 ,整体准确率是90%,而实际上0全部预测为1,错误率100%,而1的准确率是100%
逻辑回归模型主要应用场景就是二分类问题:比如是不是垃圾邮件,是猫还是狗
神经网络模型也是基于此原理实现的
-
截图0赞 · 0采集










