-
 xiao_li_hua
2024-05-02
xiao_li_hua
2024-05-02
- 好可惜,好可惜
不可惜不可惜
- 1回答·218浏览
-
 Linusu
2020-09-28
Linusu
2020-09-28
- CMap.exe 已触发了一个断点
这个还少了个/吧
- 1回答·854浏览
-
 qq_慕神4556126
2020-09-08
qq_慕神4556126
2020-09-08
- VS2019莫名其妙跳过了写的设置输出节点为已访问这个语句
没有贴代码!无法知道你是什么原因导致地死循环
- 1回答·1011浏览
-
 weixin_慕仙449830
2020-08-27
weixin_慕仙449830
2020-08-27
- 是否没考虑到闭合的问题
视频一开始就提及了关于是否可以纳入已选边集合的条件:判断现有边是否已经形成闭环,如果是则舍弃。
- 1回答·753浏览
-
 慕神6053403
2020-02-12
慕神6053403
2020-02-12
- Edge.h Edge.cpp里面是啥
醉了,我怎么直接看的kruskal
- 1回答·1052浏览
-
 慕慕9573698
2020-02-10
慕慕9573698
2020-02-10
- 最小边的点集合问题
这是克鲁斯卡尔算法的原理啊
在邻接矩阵里取出所有边后找出最小边
最小边对应的点不在集合中则添加进去
一个在的话则把另一个添加到该点集合中
两个都在同一个点集合中,只能抛弃这条边,为什么呢?因为会形成回环。例如:有一个点集合为{A,B,C},要找的边为AC,对应两个点都在,再选AC这条边的话A-B,B-C,A-C就形成回环,所以在程序里continue跳过
两个点在不同的点集合中,说明这两个点集合代表的边可以通过当前这条边连接起来,对应程序里的处理就是拼接两个vector
- 1回答·1055浏览
-
 慕慕9573698
2020-02-10
慕慕9573698
2020-02-10
- linux下出现段错误
这样大家没法判断你出的是什么错呀朋友,这句代码本身没有错的。
- 1回答·904浏览
-
 慕慕9573698
2020-02-09
慕慕9573698
2020-02-09
- 为什么我在linux下运行代码会出现段错误,代码和老师的一样
段错误一般都是内存问题导致的。 你要检查下首先是不是内存不足,或者说你程序有没有存在内存泄漏。
- 1回答·1128浏览
-
 无职转生
2019-09-16
无职转生
2019-09-16
- 深度优先遍历解答
111
- 1回答·885浏览
-
 慕数据6161364
2019-08-30
慕数据6161364
2019-08-30
- 请教!我出现了一大堆undefined reference to错误是这么回事?
检测一下的类名有没有写正确?
- 1回答·1034浏览
-
 国宝阿宝
2019-08-15
国宝阿宝
2019-08-15
- 广度优先遍历中,老师说“当前节点中的一个节点”,又说“上一层节点当中其中一个节点”,这什么意思?
想明白了。应该以“这一层”和“下一层”的说法来说好理解一些,毕竟以“上一层”来说,是以正在查找的和preVec里的节点有连接的节点所构成的一层节点为参照点,然而这一层节点是不一定有的。
- 1回答·1040浏览
-
 慕姐7121621
2019-08-08
慕姐7121621
2019-08-08
- 矩阵数组初始化时,为什么在构造函数里面成功了,但是一出构造函数就都变成随机数了?
按道理讲,创建动态分配的数组时是不可以初始化的,只能在后续将其所有元素逐一设置为零。
所以,在构造函数中创建完矩阵数组后,是需要给数组全部元素赋值为零的。否则就是随机数。
有个便捷函数是:memset(m_pMatrix, 0, m_iCapacity *m_iCapacity * sizeof(int));。教程里面也有的。
- 2回答·1091浏览
-
 qq_慕斯卡2428267
2019-07-27
qq_慕斯卡2428267
2019-07-27
- 关于老师提到的最后一个问题
你的意思是在for (int i = 0; i < m_iCapacity; i++)前用
m_pNodeArray[temp].m_bIsVisited =true;吗?这样效果是一样的,当把点放进去时就已经用到了,等下加下一个的时候才设置为已访问有点说不过去- 1回答·944浏览
-
 qq_池鱼_4
2019-03-18
qq_池鱼_4
2019-03-18
- 为什么我的广度优先先打印了 8
这个图
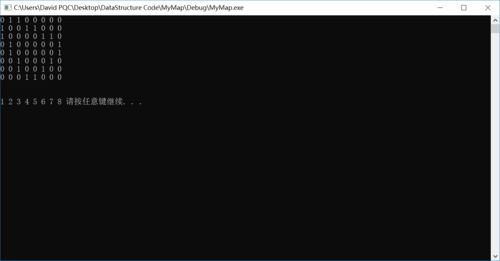
- 2回答·1135浏览
-
 慕斯卡4155732
2018-12-31
慕斯卡4155732
2018-12-31
- 深度优先遍历函数如何在搜索到F后再转到D的
想通了,递归调用实际上是一个嵌套循环,它需要一层一层的从内将每一个for循环执行完再跳出当前循环,直到跳到第一个for循环,并继续执行下去。这个时候nodeIndex=0,i=2,再在第一行寻找下一个点即D
- 1回答·1196浏览
-
 我不要我不要
2018-12-17
我不要我不要
2018-12-17
- 集合的合并问题
顶顶顶
- 1回答·1211浏览
-
 我是你的大叔啊
2018-12-04
我是你的大叔啊
2018-12-04
- 只输出一个A
m_pEdge[edgeCount] = edgeVec[edgeIndex];
edgeCount++;
不是nodeIndex
- 2回答·967浏览
-
 慕仰3095686
2018-11-29
慕仰3095686
2018-11-29
- 箭头和点的区别
箭头是指针方式,点是索引方式。这里m_pNodeArray[m_iNodeCount].m_cData=...是为数组赋值
- 2回答·1234浏览
-
 Cocoabeans
2018-08-12
Cocoabeans
2018-08-12
- 关于这种思路的局限性
- 已采纳 晴天cloude 的回答
广度优先遍历是一层一层的遍历,同层节点之间的输出顺序与矩阵的排列有关,也就是和一开始节点的输入顺序有关,但是同层节点的输出顺序并不是广度优先搜索的重点。
当然要是非按照固定的一种顺序,在输入节点的代码上写个排序就行了。
- 1回答·1636浏览
-
 阿星灬
2018-07-30
阿星灬
2018-07-30
- 为什么demo里 CMap 用new申请的内存在结束时 不需要用delete释放呢:Node也是
这是创建的对象指针,对象的周期结束后会自动释放内存
- 2回答·1357浏览
-
 就只能这样了
2018-07-26
就只能这样了
2018-07-26
- getvalue函数第三个参数是引用
引用是为了获取这个引用参数,而不是作为形参使用。
比如在其他面向对象语言中,需要一个数值,就用return value返回,
C++支持获取引用的参数,这样可以不用为了获取某种类型的值而改变方法返回参数类型
- 1回答·1522浏览
-
 慕无忌5762020
2018-07-21
慕无忌5762020
2018-07-21
- 算法编码问题
标记啊,标记哪些点被访问过,这样就遇到被访问的点会跳过,就能保证最后搜索了所有的点
//将当前点置为被访问
m_pNodeArray[nodeIndex].m_bIsVisited = true;
- 3回答·1096浏览
-
 wonder_skye
2018-07-17
wonder_skye
2018-07-17
- 普利姆算法的输出有问题,麻烦大家看看是哪里错了,谢谢!

这里应该是把nextnodeindex放进去 函数是nodevc.back(nextnodeindex) 你手误了 那样是放不进去的 这样的话 下一次还从A找 所以就错了- 1回答·1366浏览
-
 我150
2018-06-25
我150
2018-06-25
- 只学了c,能看吗
我学的Java还在看
- 2回答·1065浏览
-
 我150
2018-06-25
我150
2018-06-25
-
 qq_I個ren_0
2018-05-29
qq_I個ren_0
2018-05-29
- 克鲁斯卡尔算法的循环条件应该是看某个点集是否包含所有点吧,不应该是看边的数量吧?
看边的数量的话也是可以的,因为不形成闭环,N-1 条边是一定与N个点相连接的。
- 3回答·1607浏览
-
 慕侠3348009
2018-04-30
慕侠3348009
2018-04-30
- 形成闭环是怎么回事?
- 已采纳 qq_191_0 的回答
这个等式表明两个结点位于同一集合里。这能够得到这两个结点可以通过其他结点相连的结论,所以如果A,B再直接相连便会形成闭环
- 1回答·3003浏览
-
 小俊199641
2018-04-26
小俊199641
2018-04-26
- 请问数据结构之探险篇
- 已采纳 幕布斯9075980 的回答
void CMap::kruskalTree()
{
int value = 0;
int edgeCount = 0;
vector<vector<int>> nodeSets;
//之前一直显示vector subscript out of range,这是因为后面出现对vector直接取vec[]的语句,这是不对的
//因为vector没有分配空间,我在这里分配空间后就可以了。
nodeSets.resize(m_iCapacity*m_iCapacity);
vector<Edge>edgeVec;
for (int i = 0; i < m_iCapacity; i++)
{
for (int k = i+1; k < m_iCapacity; k++)
{
getValueFromMatrix(i, k, value);
if (value != 0)
{
Edge edge(i,k, value);
edgeVec.push_back(edge);
}
}
}
//1.找出算法结束条件
while (edgeCount < m_iCapacity -1)
{
//2从边集合中找出最小边
int minEdgeIndex = getMinEdge(edgeVec);
edgeVec[minEdgeIndex].m_bSelected = true;
//3找出连接最小边的点
int nodeAIndex = edgeVec[minEdgeIndex].m_iNodeIndexA;
int nodeBIndex = edgeVec[minEdgeIndex].m_iNodeIndexB;
//4找出点所在的点的集合
bool nodeAIsInSet = false;
bool nodeBIsInSet = false;
int nodeAInSetLabel = -1;
int nodeBInSetLabel = -1;
for (int i = 0; i < (int)nodeSets.size(); i++)
{
nodeAIsInSet = IsInset(nodeSets[i], nodeAIndex);
if (nodeAIsInSet)//点在指定的集合中
{
nodeAInSetLabel = i;//A点所在的点集合的索引
}
}
for (int i = 0; i < (int)nodeSets.size(); i++)
{
nodeBIsInSet = IsInset(nodeSets[i], nodeBIndex);
if (nodeBIsInSet)//点在指定的集合中
{
nodeBInSetLabel = i;//A点所在的点集合的索引
}
}
//5根据点所在的集合的不同做出不同的处理
if (nodeAInSetLabel == -1 && nodeBInSetLabel == -1)
{
vector<int>vec;
vec.push_back(nodeAIndex);
vec.push_back(nodeBIndex);
nodeSets.push_back(vec);
}
else
if (nodeAInSetLabel == -1 && nodeBInSetLabel != -1)//A不在任何集合中
{
nodeSets[nodeBIndex].push_back(nodeAIndex);
}
else
if (nodeAInSetLabel != -1 && nodeBInSetLabel == -1)
{
nodeSets[nodeAIndex].push_back(nodeBIndex);
}
else
if (nodeAInSetLabel != -1 && nodeBInSetLabel != -1 && nodeAInSetLabel != nodeBInSetLabel)
{
mergeNodeSet(nodeSets[nodeAIndex], nodeSets[nodeBIndex]);//把B合并到A当中,B销毁
for (int k = nodeBInSetLabel; k < (int)nodeSets.size()-1; k++)
{
nodeSets[k] = nodeSets[k + 1];
}
}
else
if (nodeAInSetLabel != -1 && nodeBInSetLabel != -1 && nodeAInSetLabel == nodeBInSetLabel)
{
continue;
}
m_pEdge[edgeCount] = edgeVec[minEdgeIndex];//保存边
edgeCount++;
cout << edgeVec[minEdgeIndex].m_iNodeIndexA << "-------------" << edgeVec[minEdgeIndex].m_iNodeIndexB << " ";
cout << edgeVec[minEdgeIndex].m_iWeightValue << endl;
}
}
- 1回答·1273浏览
-
 小俊199641
2018-04-26
小俊199641
2018-04-26
- 请问有没有图源代码
https://github.com/silenceccm/Data-structure-graph
- 2回答·1266浏览
-
 慕侠3348009
2018-04-26
慕侠3348009
2018-04-26
- 为什么还要在主对角线上赋值,第一个语句不能全部赋值吗?
主对角线的元素是顶点到自己的 自己与自己是没有连线的 上面的两个代码就是对应于无向图所说的 因为无向图隐含的就是每个顶点都有两条弧 所以就是对称矩阵 只要有连线的都要进行赋权值。
- 2回答·1328浏览























