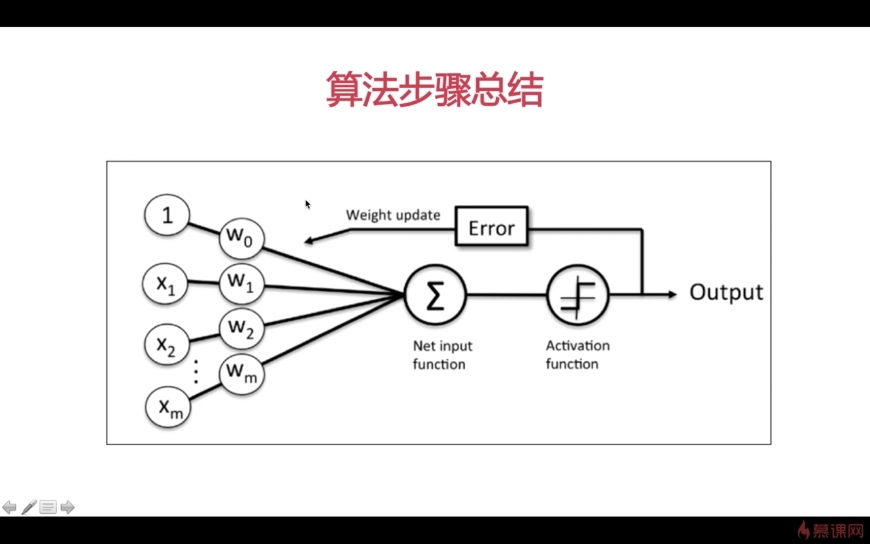
感知器分类算法叽叽叽叽叽叽

．

感知器数据分类算法步骤：

1、把权重向量W初始化为0，或把每个分量初始化为【0,1】间任意小数

2、把训练样本输入感知器，得到分类结果（-1或1）

根据分类结果更新权重向量

阈值的更新

感知器算法试用范围

权重更新算法

ada = AdalineGD(eta = 0.001, n_iter = 50)
ada.fit(x, y)
plot_decision_region(x, y, classifier = ada)
plt.title('Adaline-Gradient decent')
plt.xlabel('the length of huajing')
plt.ylabel('the length of huaban')
plt.legend(loc='upper left')
plt.show()

class AdalineGD(object):
    def __init__(self, eta, n_iter):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):
        self.w_ = np.zeros(1 + X.shape[1])
        self.cost_ []
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = y - output
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors ** 2).sum() / 2.0
            self.cost_.append(cost)
        return self
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]
    def activation(self, X):
        return self.net_input(X)
    def predict(self, X):
        return np.where(self.activation(X) >= 0, 1, -1)

η是前面提到的学习率，μ=-η。

倒数第三行，求和符号下面的是j，不是i。

对w求偏导，会得到一条切线的斜率k，当在U形图左半部的时候，k<0，增大w的值，在在右半部的时候，k>0，减小w的值，就会找到J(w)的最小值。

不断调整w0-wm，使得J(w)的值最小，对神经元的训练效果才最好。

感知器的激活函数是步调函数，输入值大于给定的阈值输出1，小于输出0。自适应线性神经元激活函数是1*w0+x1*w1+... 点积求和的计算结果与正确的结果比较

from matplotlib.colors import ListedColormap
def plot_decision_region(X, y, classifier, resolution=0.02):
    marker = ('s', 'x', 'o', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListColormap(colors[:len(np.unique(y))])
    
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max()
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max()
    
    # 将np.arange()中的向量扩展成一个矩阵
    '''
    xx1:
    a = np.arange(x1_min, x1_max, resolution) 向量元素为185个
    xx1[255, 185],将a中的元素作为一行，重复255行
    xx2:
    b = np.arange(x2_min, x2_max, resolution) 向量元素为255个
    xx2[255, 185],将b中的元素作为一列，重复185列
    '''
    xx1, xx2 = np.mesbgrid(np.arange(x1_min, x1_max, resolution),
                           np.arrange(x2_min, x2_max, resolution))

file = "iris.csv"
import pandas as pd # 数据读取类库
# header指定文件是否有表头
df = pd.read_csv(file, header = None)
# 显示文件前十行
df,head(10)
import matplotlib.pyplot as plt
import numpy as np
# 得到数据前一百行的第五列
y = df.loc[0:100, 4].values
print(y)
# 将字符串转化为数字
y = np.where(y == 'Iris-setosa', -1, 1)
# 抽取数据第0列和第2列
x = df,iloc[0:100, [0, 2]].values
# scatter散列点绘图
plt.scatter(x[:50, 0], x[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(x[50:100, 0], x[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('花瓣长度')
plt.ylabel('花茎长度')
plt.legend(loc='upper left')
plt.show()

import numpy as np
class Perceptron(object):
    def __init__(self, eta = 0.01, n_iter = 10):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):
        self.w_ = np.zero(1 + X.shape[1])
        self.error_ = []
        for _ in range(self.n_iter):
            errors = 0
            '''
            X:[[1, 2, 3], [4, 5, 6]
            y:[1, -1]
            zip(X, y):[[1, 2, 3, 1]. [4, 5, 6, -1]]
            '''
            for xi, target in zip(X, y):
                '''
                update = n * (y - y')
                '''
                update = self.eta * (target - self.predict(xi))
                '''
                xi是一个向量
                update * xi等价于
                [w1 = x1*update, w2 = x2*update, ......]
                '''
                self.w_[1:] += update * xi
                self.w_[0] += update
                errors += int(update != 0.0)
                self.errors_.append(errors)
        def net_input(self, X):
            '''
            z = w0*1 + w1*x1 + w2*x2 +.....
            np.dot()是做点积
            '''
            return np.dot(X, self.w_[1:]) + self.w_[0]
        def predict(self, X):
            return np.where(self.net_input(X) >= 0.0, 1, -1)

import numpy as np
class Perceptron(object):
    '''
    eta：学习率
    n_iter：权重向量的训练次数
    w_：神经分叉权重向量
    errors_：用于记录神经元判断出错次数
    '''
    def __init__(self, eta = 0.01, n_iter = 10);
        self.eta = eta
        self,n_iter = n_iter
    def fit(self, X, y):
        '''
        输入训练数据，培训神经元
        X是输入样本向量，y是对应的样本分类
        X:shape[n_samples, n_features]
        X:[[1, 2, 3], [4, 5, 6]]
        n_samples: 2
        n_features: 3
        y:[1, -1]
        '''
        #初始化权重向量为0，加1是因为提到的w0,即步调函数的阈值
        self.w_ = np.zero(1 + X.shape[1])
        self.errora_ = []

适用范围：预测的数据是可以进行线性分割的

感知器的隐含层是点积求和函数

权重更新算法

学习率是训练者人为设置的

右侧的关于z的函数就是感知器

感知器数据分类算法步骤

分类算法大致有两种类型：感知器；适应性的线性神经元。

算法步骤

神经网络数学概念

人工神经元

x(j)电信号

当感知器计算出错误的分类，才需要调整权重W(j)

W（j）模型自动改进

η需要使用者根据具体的使用场景，基于经验来调整

步调函数（激活）与阈值

感知器数据分类算法步骤