本文源地址http://www.fullstackyang.com/...转发请注明该地址或segmentfault地址谢谢

微信公众号发布的文章和一般门户网站的新闻文本类型有所不同通常不能用现有的文本分类器直接对这些文章进行分类不过文本分类的原理是相通的本文以微信公众号文章为对象介绍朴素贝叶斯分类器的实现过程。

文本分类的科学原理和数学证明在网上有很多这里就不做赘述本文尽量使用通熟易懂的表述方式简明扼要地梳理一下文本分类器的各个知识点。

参考了一下Github发现少有Java 8风格的实现所以这里的实现尽量利用Java 8的特性相比之前优势有很多例如stream在统计聚合等运算上比较方便代码不仅简洁而且更加语义化另外在多线程并行控制上也省去不少的工作。

本项目的地址https://github.com/fullstacky...

一、文本分类器的概述

文本分类器可以看作是一个预测函数在给定的文本时在预定的类别集合中判断该文本最可能属于哪个类。

这里需要注意两个问题

在文本中含有比较多的标点符号和停用词的是了等直接使用整段文本处理肯定会产生很多不必要的计算而且计算量也非常大因此需要把给定的文本有效地进行表示也就是选择一系列的特征词来代表这篇文本这些特征词既可以比较好地反应所属文本的内容又可以对不同文本有比较好的区分能力。
在进行文本表示之后如何对这些特征词进行预测这就是分类器的算法设计问题了比较常见的模型有朴素贝叶斯基于支持向量机SVMK-近邻KNN决策树等分类算法。这里我们选择简单易懂的朴素贝叶斯算法。在机器学习中朴素贝叶斯建模属于有监督学习因此需要收集大量的文本作为训练语料并标注分类结果

综上实现一个分类器通常分为以下几个步骤

收集并处理训练语料以及最后测试用的测试语料
在训练集上进行特征选择得到一系列的特征项词这些特征项组成了所谓的特征空间
为了表示某个特征项在不同文档中的重要程度计算该特征项的权重常用的计算方法有TF-IDF本文采用的是“经典”朴素贝叶斯模型这里不考虑特征项的权重当然一定要做也可以
训练模型对于朴素贝叶斯模型来说主要的是计算每个特征项在不同类别中的条件概率这点下面再做解释。
预测文本模型训练完成之后可以保存到文件中在预测时直接读入模型的数据进行计算。

二、准备训练语料

这里需要的语料就是微信公众号的文章我们可以抓取搜狗微信搜索网站http://weixin.sogou.com/首页上已经分类好的文章直接采用其分类结果这样也省去了标注的工作。至于如何开发爬虫去抓取文章这里就不再讨论了。

“热门”这类别下的文章不具有一般性因此不把它当作一个类别。剔除“热门”类别之后最终我们抓取了30410篇文章总共20个类别每个类别的文章数并不均衡其中最多的是“养生堂”类别有2569篇文章最少的是“军事”类别有654篇大体符合微信上文章的分布情况。在保存时我们保留了文章的标题公众号名称文章正文。

三、特征选择

如前文所述特征选择的目的是降低特征空间的维度避免维度灾难。简单地说假设我们选择了2万个特征词也就是说计算机通过学习得到了一张有2万个词的“单词表”以后它遇到的所有文本可以够用这张单词表中的词去表示其内容大意。这些特征词针对不同的类别有一定的区分能力举例来说“歼击机”可能来自“军事”“越位”可能来自“体育”“涨停”可能来自“财经”等等而通常中文词汇量要比这个数字大得多一本常见的汉语词典收录的词条数可达数十万。

常见的特征选择方法有两个信息增益法和卡方检验法。

3.1 信息增益

信息增益法的衡量标准是这个特征项可以为分类系统带来多少信息量所谓的信息增益就是该特征项包含的能够帮预测类别的信息量这里所说的信息量可以用熵来衡量计算信息增益时还需要引入条件熵的概念公式如下

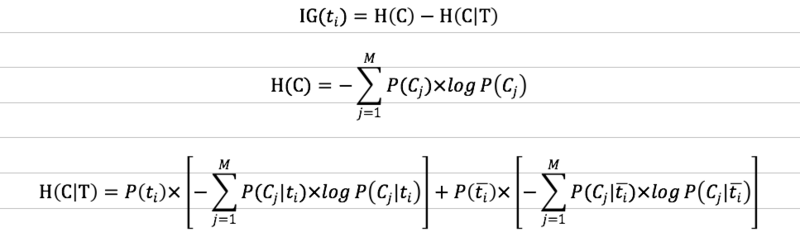
可能有些见到公式就头大的小伙伴不太友好不过这个公式虽然看起来有点复杂其实在计算中还是比较简单的解释一下

P(Cj)Cj类文档在整个语料中出现的概率

P(ti)语料中包含特征项ti的文档的概率取反就是不包含特征项ti的文档的概率

P(Cj|ti)文档包含特征项ti且属于Cj类的条件概率取反就是文档不包含特征项ti且属于Cj类的条件概率

上面几个概率值都可以比较方便地从训练语料上统计得到。若还有不明白的小伙伴推荐阅读这篇博客文本分类入门十一特征选择方法之信息增益

3.2 卡方检验

卡方检验基于χ2统计量(CHI)来衡量特征项ti和类别Cj之间的相关联程度CHI统计值越高该特征项与该类的相关性越大如果两者相互独立则CHI统计值接近零。计算时需要根据一张相依表contingency table公式也比较简单

其中N就是文档总数如果想继续讨论这个公式推荐阅读这篇博客特征选择3-卡方检验

3.3 算法实现

不论何种方式都需要对每个特征项进行估算然后根据所得的数值进行筛选通常可以设定一个阈值低于阈值的特征项可以直接从特征空间中移除另外也可以按照数值从高到低排序并指定选择前N个。这里我们采用后者总共截取前2万个特征项。

特征选择实现类的代码如下其中不同特征选择方法需实现Strategy接口以获得不同方法计算得到的估值这里在截取特征项时为了避免不必要的麻烦剔除了字符串长度为1的词。

Doc对象表示一篇文档其中包含了该文档的所属分类以及分词结果已经滤掉了停用词等即Term集合

Term对象主要包含3个字段词本身的字符串词性用于过滤词频TF

Feature表示特征项一个特征项对应一个Term对象还包含两个hashmap一个用来统计不同类别下该特征项出现的文档数量categoryDocCounter另一个用来统计不同类别下该特征项出现的频度categoryTermCounter对应朴素贝叶斯两种不同模型下文详述

统计时引入FeatureCounter对象使用stream的reduce方法进行归约。主要的思想就是把每一个文档中的Term集合映射为Term和Feature的键值对然后再和已有的Map进行合并合并时如果遇到相同的Term则调用Feature的Merge方法该方法会将双方term的词频以及categoryDocCounter和categoryTermCounter中的统计结果进行累加。最终将所有文档全部统计完成返回Feature集合。

@AllArgsConstructor public class FeatureSelection {     interface Strategy {         Feature estimate(Feature feature);     }     private final Strategy strategy;     private final static int FEATURE_SIZE = 20000;     public List<Feature> select(List<Doc> docs) {         return createFeatureSpace(docs.stream())                 .stream()                 .map(strategy::estimate)                 .filter(f -> f.getTerm().getWord().length() > 1)                 .sorted(comparing(Feature::getScore).reversed())                 .limit(FEATURE_SIZE)                 .collect(toList());     }     private Collection<Feature> createFeatureSpace(Stream<Doc> docs) {         @AllArgsConstructor         class FeatureCounter {             private final Map<Term, Feature> featureMap;             private FeatureCounter accumulate(Doc doc) {                 Map<Term, Feature> temp = doc.getTerms().parallelStream()                         .map(t -> new Feature(t, doc.getCategory()))                         .collect(toMap(Feature::getTerm, Function.identity()));                 if (!featureMap.isEmpty())                     featureMap.values().forEach(f -> temp.merge(f.getTerm(), f, Feature::merge));                 return new FeatureCounter(temp);             }             private FeatureCounter combine(FeatureCounter featureCounter) {                 Map<Term, Feature> temp = Maps.newHashMap(featureMap);                 featureCounter.featureMap.values().forEach(f -> temp.merge(f.getTerm(), f, Feature::merge));                 return new FeatureCounter(temp);             }         }         FeatureCounter counter = docs.parallel()                 .reduce(new FeatureCounter(Maps.newHashMap()),                         FeatureCounter::accumulate,                         FeatureCounter::combine);         return counter.featureMap.values();     } } public class Feature { ...     public Feature merge(Feature feature) {         if (this.term.equals(feature.getTerm())) {             this.term.setTf(this.term.getTf() + feature.getTerm().getTf());             feature.getCategoryDocCounter()                     .forEach((k, v) -> categoryDocCounter.merge(k, v, (oldValue, newValue) -> oldValue + newValue));             feature.getCategoryTermCounter()                     .forEach((k, v) -> categoryTermCounter.merge(k, v, (oldValue, newValue) -> oldValue + newValue));         }         return this;     } }

信息增益实现如下在计算条件熵时利用了stream的collect方法将包含和不包含特征项的两种情况用一个hashmap分开再进行归约。

@AllArgsConstructor public class IGStrategy implements FeatureSelection.Strategy {     private final Collection<Category> categories;     private final int total;     public Feature estimate(Feature feature) {         double totalEntropy = calcTotalEntropy();         double conditionalEntrogy = calcConditionEntropy(feature);         feature.setScore(totalEntropy - conditionalEntrogy);         return feature;     }     private double calcTotalEntropy() {         return Calculator.entropy(categories.stream().map(c -> (double) c.getDocCount() / total).collect(toList()));     }     private double calcConditionEntropy(Feature feature) {         int featureCount = feature.getFeatureCount();         double Pfeature = (double) featureCount / total;         Map<Boolean, List<Double>> Pcondition = categories.parallelStream().collect(() -> new HashMap<Boolean, List<Double>>() {{                     put(true, Lists.newArrayList());                     put(false, Lists.newArrayList());                 }}, (map, category) -> {                     int countDocWithFeature = feature.getDocCountByCategory(category);                     //出现该特征词且属于类别key的文档数量/出现该特征词的文档总数量                     map.get(true).add((double) countDocWithFeature / featureCount);                     //未出现该特征词且属于类别key的文档数量/未出现该特征词的文档总数量                     map.get(false).add((double) (category.getDocCount() - countDocWithFeature) / (total - featureCount));                 },                 (map1, map2) -> {                     map1.get(true).addAll(map2.get(true));                     map1.get(false).addAll(map2.get(false));                 }         );         return Calculator.conditionalEntrogy(Pfeature, Pcondition.get(true), Pcondition.get(false));     } }

卡方检验实现如下每个特征项要在每个类别上分别计算CHI值最终保留其最大值

@AllArgsConstructor public class ChiSquaredStrategy implements Strategy {     private final Collection<Category> categories;     private final int total;     @Override     public Feature estimate(Feature feature) {         class ContingencyTable {             private final int A, B, C, D;             private ContingencyTable(Feature feature, Category category) {                 A = feature.getDocCountByCategory(category);                 B = feature.getFeatureCount() - A;                 C = category.getDocCount() - A;                 D = total - A - B - C;             }         }         Double chisquared = categories.stream()                 .map(c -> new ContingencyTable(feature, c))                 .map(ct -> Calculator.chisquare(ct.A, ct.B, ct.C, ct.D))                 .max(Comparator.comparingDouble(Double::valueOf)).get();         feature.setScore(chisquared);         return feature;     } }

四、朴素贝叶斯模型

4.1 原理简介

朴素贝叶斯模型之所以称之“朴素”是因为其假设特征之间是相互独立的在文本分类中也就是说一篇文档中出现的词都是相互独立彼此没有关联显然文档中出现的词都是有逻辑性的这种假设在现实中几乎是不成立的但是这种假设却大大简化了计算根据贝叶斯公式文档Doc属于类别Ci的概率为

P(Ci|Doc)是所求的后验概率我们在判定分类时根据每个类别计算P(Ci|Doc)最终把P(Ci|Doc)取得最大值的那个分类作为文档的类别。其中P(Doc)对于类别Ci来说是常量在比较大小时可以不用参与计算而P(Ci)表示类别Ci出现的概率我们称之为先验概率这可以方便地从训练集中统计得出至于P(Doc|Ci)也就是类别的条件概率如果没有朴素贝叶斯的假设那么计算是非常困难的。

举例来说假设有一篇文章内容为“王者荣耀两款传说品质皮肤将优化李白最新模型海报爆料”经过特征选择文档可以表示为Doc=(王者荣耀传说品质皮肤优化李白最新模型海报爆料)那么在预测时需要计算P(王者荣耀传说品质皮肤优化李白最新模型海报爆料|Ci)这样一个条件概率是不可计算的因为第一个特征取值为“王者荣耀”第二个特征取值“传说”……第十个特征取值“爆料”的文档很可能为没有那么概率就为零而基于朴素贝叶斯的假设这个条件概率可以转化为

P(王者荣耀传说品质皮肤优化李白最新模型海报爆料|Ci)=P(王者荣耀|Ci)

P(传说|Ci)……

P(爆料|Ci)

于是我们就可以统计这些特征词在每个类别中出现的概率了在这个例子中游戏类别中“王者荣耀”这个特征项会频繁出现因此P(王者荣耀|游戏)的条件概率要明显高于其他类别这就是朴素贝叶斯模型的朴素之处粗鲁的聪明。

4.2 多项式模型与伯努利模型

在具体实现中朴素贝叶斯又可以分为两种模型多项式模型Multinomial和伯努利模型Bernoulli另外还有高斯模型主要用于处理连续型变量在文本分类中不讨论。

多项式模型和伯努利模型的区别在于对词频的考察在多项式模型中文档中特征项的频度是参与计算的这对于长文本来说是比较公平的例如上面的例子“王者荣耀”在游戏类的文档中频度会比较高而伯努利模型中所有特征词都均等地对待只要出现就记为1未出现就记为0两者公式如下

在伯努利模型计算公式中N(Doc(tj)|Ci)表示Ci类文档中特征tj出现的文档数|D|表示类别Ci的文档数P(Ci)可以用类别Ci的文档数/文档总数来计算

在多项式模型计算公式中TF(ti,Doc)是文档Doc中特征ti出现的频度TF(ti,Ci)就表示类别Ci中特征ti出现的频度|V|表示特征空间的大小也就是特征选择之后不同即去掉重复之后的特征项的总个数而P(Ci)可以用类别Ci中特征词的总数/所有特征词的总数所有特征词的总数也就是所有特征词的词频之和。

至于分子和分母都加上一定的常量这是为了防止数据稀疏而产生结果为零的现象这种操作称为拉普拉斯平滑至于背后的原理推荐阅读这篇博客贝叶斯统计观点下的拉普拉斯平滑

4.3 算法实现

这里使用了枚举类来封装两个模型并实现了分类器NaiveBayesClassifier和训练器NaiveBayesLearner中的两个接口其中Pprior和Pcondition是训练器所需的方法前者用来计算先验概率后者用来计算不同特征项在不同类别下的条件概率getConditionProbability是分类器所需的方法NaiveBayesKnowledgeBase对象是模型数据的容器它的getPconditionByWord方法就是用于查询不同特征词在不同类别下的条件概率

public enum NaiveBayesModels implements NaiveBayesClassifier.Model, NaiveBayesLearner.Model {     Bernoulli {         @Override         public double Pprior(int total, Category category) {             int Nc = category.getDocCount();             return Math.log((double) Nc / total);         }         @Override         public double Pcondition(Feature feature, Category category, double smoothing) {             int Ncf = feature.getDocCountByCategory(category);             int Nc = category.getDocCount();             return Math.log((double) (1 + Ncf) / (Nc + smoothing));         }         @Override         public List<Double> getConditionProbability(String category, List<Term> terms, final NaiveBayesKnowledgeBase knowledgeBase) {             return terms.stream().map(term -> knowledgeBase.getPconditionByWord(category, term.getWord())).collect(toList());         }     },     Multinomial {         @Override         public double Pprior(int total, Category category) {             int Nt = category.getTermCount();             return Math.log((double) Nt / total);         }         @Override         public double Pcondition(Feature feature, Category category, double smoothing) {             int Ntf = feature.getTermCountByCategory(category);             int Nt = category.getTermCount();             return Math.log((double) (1 + Ntf) / (Nt + smoothing));         }         @Override         public List<Double> getConditionProbability(String category, List<Term> terms, final NaiveBayesKnowledgeBase knowledgeBase) {             return terms.stream().map(term -> term.getTf() * knowledgeBase.getPconditionByWord(category, term.getWord())).collect(toList());         }     }; }

五、训练模型

根据朴素贝叶斯模型的定义训练模型的过程就是计算每个类的先验概率以及每个特征项在不同类别下的条件概率NaiveBayesKnowledgeBase对象将训练器在训练时得到的结果都保存起来训练完成时写入文件启动分类时从文件中读入数据交由分类器使用那么在分类时就可以直接参与到计算过程中。

训练器的实现如下

public class NaiveBayesLearner {     ……     ……     public NaiveBayesLearner statistics() {         log.info("开始统计...");         this.total = total();         log.info("total : " + total);         this.categorySet = trainSet.getCategorySet();         featureSet.forEach(f -> f.getCategoryTermCounter().forEach((category, count) -> category.setTermCount(category.getTermCount() + count)));         return this;     }     public NaiveBayesKnowledgeBase build() {         this.knowledgeBase.setCategories(createCategorySummaries(categorySet));         this.knowledgeBase.setFeatures(createFeatureSummaries(featureSet, categorySet));         return knowledgeBase;     }     private Map<String, NaiveBayesKnowledgeBase.FeatureSummary> createFeatureSummaries(final Set<Feature> featureSet, final Set<Category> categorySet) {         return featureSet.parallelStream()                 .map(f -> knowledgeBase.createFeatureSummary(f, getPconditions(f, categorySet)))                 .collect(toMap(NaiveBayesKnowledgeBase.FeatureSummary::getWord, Function.identity()));     }     private Map<String, Double> createCategorySummaries(final Set<Category> categorySet) {         return categorySet.stream().collect(toMap(Category::getName, c -> model.Pprior(total, c)));     }     private Map<String, Double> getPconditions(final Feature feature, final Set<Category> categorySet) {         final double smoothing = smoothing();         return categorySet.stream()                 .collect(toMap(Category::getName, c -> model.Pcondition(feature, c, smoothing)));     }     private int total() {         if (model == Multinomial)             return featureSet.parallelStream().map(Feature::getTerm).mapToInt(Term::getTf).sum();//总词频数         else if (model == Bernoulli)             return trainSet.getTotalDoc();//总文档数         return 0;     }     private double smoothing() {         if (model == Multinomial)             return this.featureSet.size();         else if (model == Bernoulli)             return 2.0;         return 0.0;     }     public static void main(String[] args) {         TrainSet trainSet = new TrainSet(System.getProperty("user.dir") + "/trainset/");         log.info("特征选择开始...");         FeatureSelection featureSelection = new FeatureSelection(new ChiSquaredStrategy(trainSet.getCategorySet(), trainSet.getTotalDoc()));         List<Feature> features = featureSelection.select(trainSet.getDocs());         log.info("特征选择完成,特征数:[" + features.size() + "]");         NaiveBayesModels model = NaiveBayesModels.Multinomial;         NaiveBayesLearner learner = new NaiveBayesLearner(model, trainSet, Sets.newHashSet(features));         learner.statistics().build().write(model.getModelPath());         log.info("模型文件写入完成,路径:" + model.getModelPath());     } }

在main函数中执行整个训练过程首先执行特征选择这里使用卡方检验法然后将得到特征空间朴素贝叶斯模型多项式模型以及训练集TrainSet对象作为参数初始化训练器接着训练器开始进行统计的工作事实上有一部分的统计工作在初始化训练集对象时就已经完成了例如总文档数每个类别下的文档数等这些可以直接拿过来使用最终将数据都装载到NaiveBayesKnowledgeBase对象当中去并写入文件格式为第一行是不同类别的先验概率余下每一行对应一个特征项每一列对应不同类别的条件概率值。

六测试模型

分类器预测过程就相对于比较简单了通过NaiveBayesKnowledgeBase读入数据然后将指定的文本进行分词匹配特征项然后计算在不同类别下的后验概率返回取得最大值对应的那个类别。

public class NaiveBayesClassifier {     ……     private final Model model;     private final NaiveBayesKnowledgeBase knowledgeBase;     public NaiveBayesClassifier(Model model) {         this.model = model;         this.knowledgeBase = new NaiveBayesKnowledgeBase(model.getModelPath());     }     public String predict(String content) {         Set<String> allFeatures = knowledgeBase.getFeatures().keySet();         List<Term> terms = NLPTools.instance().segment(content).stream()                 .filter(t -> allFeatures.contains(t.getWord())).distinct().collect(toList());         @AllArgsConstructor         class Result {             final String category;             final double probability;         }         Result result = knowledgeBase.getCategories().keySet().stream()                 .map(c -> new Result(c, Calculator.Ppost(knowledgeBase.getCategoryProbability(c),                         model.getConditionProbability(c, terms, knowledgeBase))))                 .max(Comparator.comparingDouble(r -> r.probability)).get();         return result.category;     } }

在实际测试时我们又单独抓取了搜狗微信搜索网站上的文章按照100篇一组一共30组进行分类的测试最终结果每一组的准确率均在90%以上最高达98%效果良好。当然正规的评测需要同时评估准确率和召回率这里就偷懒不做了。

另外还需要说明一点的是由于训练集是来源于搜狗微信搜索网站的文章类别仅限于这20个这不足以覆盖所有微信公众号文章的类别因此在测试其他来源的微信文章准确率一定会有所影响。当然如果有更加丰富的微信文章训练集的话也可以利用这个模型重新训练那么效果也会越来越好。

七、参考文献与引用

宗成庆. 统计自然语言处理[M]. 清华大学出版社, 2013.
T.M.Mitchell. 机器学习[M]. 机械工业出版社, 2003.
吴军. 数学之美[M]. 人民邮电出版社, 2012.
Raoul-Gabriel Urma, Mario Fusco, Alan Mycroft. Java 8 实战[M]. 人民邮电出版社, 2016.
Ansj中文分词器https://github.com/NLPchina/a...
HanLP中文分词器https://github.com/hankcs/HanLP

如何实现一个基本的微信文章分类器