一.概念
线性模型:就是线性的模型。

其实我在网上搜了很久,想用一句话能够简单易懂的表达出这个概念,但是确实不知道该怎么组织语言。不过相信有一些数学基础的同学应该是能明白的。
我们可以这样认为,世界上所有的问题都可以用公式表达,如果任何问题都是可以用线性模型来描述的,那么我们人人都可以预测未来,因为其模型非常的简单。但是很遗憾,大多数问题都是非线性的。
二.线性回归
线性回归(linearregression)通过学习到一个线性模型来尽可能准确地预测实值输出标记。这句话的意思就是说,训练出一个线性模型的学习器,然后用来预测实值输出。
常用的几种求解算法:
1.梯度下降法:沿梯度下降的方向求解极小值(也可以沿梯度上升方向求解极大值),算法迭代的终止条件是梯度向量的幅值接近0即可,可以设置个非常小的常数阈值。
C++代码
#include<iostream>#include<cmath>#include<ctime>using namespace std;double f(double x){ return x*x - 2 * x + 1;}double g(double x){ return 2 * x - 2;}double GradientDescent(double xs, double s){ double x = xs; double y; int i = 0; while(++i) { double grad = -1 * g(x); x += grad*s; y = f(x); cout << "i = " << i << " grad = " << grad << " x = " << x << " y = " << y << endl; if (abs(grad) < 1e-6) break; } return x;}int main(){ double xk = -5, ak = 0.1; GradientDescent(xk, ak); system("pause");}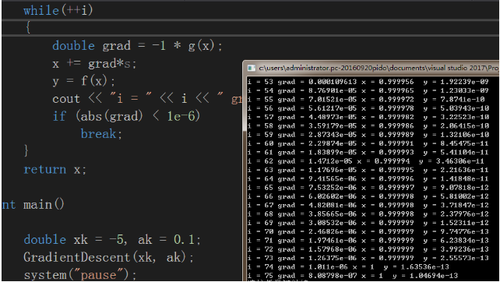
2.最小二乘法:通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
C++代码
#include<iostream>#include<cmath>using namespace std;class Point //Point类的声明{public: //外部接口 Point(float xx = 0, float yy = 0) { X = xx; Y = yy; } float GetX() { return X; } float GetY() { return Y; } friend float linefit(Point l_point[], int n_point); private: //私有数据成员 float X, Y;};float linefit(Point l_point[], int n_point) { float av_x, av_y; //声明变量 float L_xx, L_yy, L_xy; //变量初始化 av_x = 0; //X的平均值 av_y = 0; //Y的平均值 L_xx = 0; //Lxx L_yy = 0; //Lyy L_xy = 0; //Lxy for (int i = 0; i<n_point; i++) //计算X、Y的平均值 { av_x += l_point[i].X / n_point; av_y += l_point[i].Y / n_point; } for (int i = 0; i<n_point; i++) //计算Lxx、Lyy和Lxy { L_xx += (l_point[i].X - av_x)*(l_point[i].X - av_x); L_yy += (l_point[i].Y - av_y)*(l_point[i].Y - av_y); L_xy += (l_point[i].X - av_x)*(l_point[i].Y - av_y); } cout << "a=" << L_xy / L_xx << endl; //输出回归系数a cout << "b=" << av_y - L_xy*av_x / L_xx << endl; //输出回归系数b return float(L_xy / sqrt(L_xx*L_yy)); //返回相关系数r}int main(){ Point l_p[10] = { Point(208,21.6), Point(152,15.5), Point(113,10.4), Point(227,31.0), Point(137,13.0), Point(238,32.4), Point(178,19.0), Point(104,10.4), Point(191,19.0), Point(130,11.8) }; float r = linefit(l_p, 10); //进行线性回归计算 cout << "r=" << r << endl; //输出相关系数 system("pause");}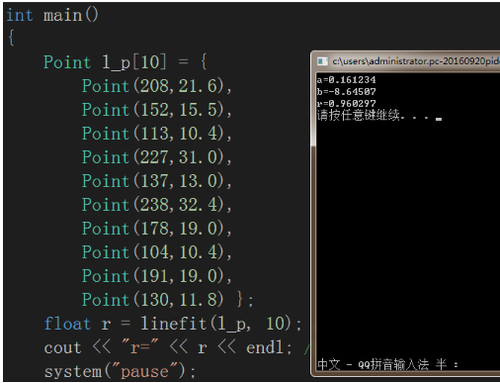
三、逻辑回归
逻辑回归(Logistic Regression, LR)其实就是在线性回归的基础上,套用了一个逻辑函数。逻辑回归是属于线性模型的,因为逻辑回归的决策边界(decision boundary)是线性的。它只是在特征到结果的映射中加入了一个sigmoid函数。即先把特征求和,然后使用非线性的函数将连续值映射到0与1之间。
逻辑回归与线性回归的差别:
1)线性回归要求变量服从正态分布,逻辑回归对变量分布没有要求。
2)线性回归要求因变量是连续性数值变量,而逻辑回归要求因变量是分类型变量。
3)线性回归要求自变量和因变量呈线性关系,而逻辑回归不要求自变量和因变量呈线性关系
4)逻辑回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
总之, 逻辑回归与线性回归实际上有很多相同之处,最大的区别就在于他们的因变量不同,其他的基本都差不多,正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalized linear model)。这一家族中的模型形式基本上都差不多,不同的就是因变量不同,如果是连续的,就是多重线性回归,如果是二项分布,就是逻辑回归。逻辑回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。所以实际中最为常用的就是二分类的逻辑回归。
四、总结
线性模型使用简单的公式通过一组数据点来查找「最优拟合」线。通过你已知的变量方程,你可以求出你想要预测的变量。为了求出预测量,我们输入已知的变量得到答案。
线性回归和逻辑回归都有着相同的缺点。两者都具有「过拟合(overfit)」的趋势,这意味着模型太适应于数据而牺牲了推广到先前未知的数据的能力。因此,这两个模型经常需要进行规范,这意味着它们有一定的惩罚(penalty)以防止过拟合。还有就是因为它们太简单了,所以往往不能预测更复杂的行为。
五、相关学习资源
https://wenku.baidu.com/view/c62809e66c85ec3a86c2c500.html
http://www.cnblogs.com/voyagflyer/p/5570446.html
http://www.sohu.com/a/128440208_465975

 随时随地看视频
随时随地看视频




