【九月打卡】第5天 Python3入门机器学习

课程名称：Python3入门机器学习 经典算法与应用 入行人工智能
课程章节：7-1
主讲老师：liuyubobobo

内容导读

---

• 第一部分 PCA简介
• 第二部分 PCA功能
• 第三部分 PCA算法实现思路
• 第四部分 代码展示

②课程详细

---

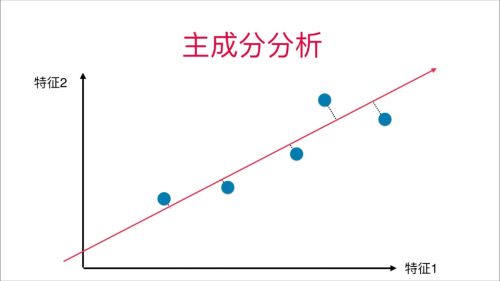
第一部分 PCA简介

PCA是为了求解一个新的空间，也就是一个新的基（坐标轴），来达到降维的目的。

第二部分 PCA功能

PCA 做的事情，就是求出了一套新的坐标轴，在新的坐标轴上，数据在每个轴上的信息含量是逐渐递减的。这样，我们就可以扔掉“靠后”的坐标轴上的信息，完成降维。

第三部分 PCA算法实现思路

波波老师这课程对数学部分并未过多介绍，主要解决思路是使用搜索的方式求解，：

目标：对X（假设4维的），要求降到2维，

1. 先对数据进行demean处理，(就是将X减去自己的平均值)(用于改变坐标轴，不影响数据分布，方便运算)
2. 找一条轴在四维空间中，能最大表现X数据的分布，记为w1，（找到了第一主成分）
3. 将原始数据X减去w1轴方向上的主成分分量，(寻找第二主成分的准备)
4. 现在X还剩下三个维度的信息，通过同样的梯度上升法找到方差最大的轴，记为w2（现在w2应该是主成分了）
5. 将原始数据X减去w2轴方向上的主成分分量.
6. 依次类推，得到，w1,w2,w3,w4,四个方向的单位向量，他们构成了一个四维空间，一个从小到大依次由最能表现X特征的四个轴组成，
7. X降到二维的话，取出单个X1，乘以w1，w2，取出单个X2，乘以w1，w2…从而得到一个二维平面，上面的数据就是，X降到二维之后特征最明显的体现。

第四部分 代码展示

导入函数

import numpy as np
import matplotlib.pyplot as plt

创造随机的数据

X = np.empty((100,2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. +np.random.normal(0,10.,size=100)

可视化数值前2维度

plt.scatter(X[:,0], X[:,1])
plt.show()

接下来就是PCA的操作过程
定义均值归一的函数，并进行均值归一，方便进行后续运算

np.mean(X, axis=0)
#array([49.74959852, 40.94159652])
#均值归零
def demean(X):
    return X - np.mean(X, axis=0)

X_demean = demean(X)

使用梯度上升法求出当前数据，最大方差的轴

def f(w, X):
    return np.sum((X.dot(w)) ** 2) / len(X)
    
def df_math(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)
    
def df_debug(w, X, epsilon=0.01):
    res = np.empty(len(w))
    for i in range(len(w)):
        w_1 = w.copy()
        w_1[i] += epsilon
        w_2 = w.copy()
        w_2[i] -=epsilon
        res[i] = (f(w_1, X) - f(w_2, X))  /(epsilon * 2)
    return res
def direction(w):
    return w / np.linalg.norm(w)

def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon = 1e-8):

    cur_iter = 0
    w = direction(initial_w)
    
    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w) 
        #对w 每次运行进行转换单位向量，用于更好的计算
        if abs(f(w, X) - f(last_w, X)) < epsilon:
            break
        cur_iter += 1
    return w

初始化数据

initial_w = np.random.random(X.shape[1])
#不能从零向量开始，应为没方向，就会一直为0
initial_w

值得一提的是（不能进行数据标准化处理，应为影响了数据的分布，从而导致最终求得得w轴方向产生偏移）
运行并可视化

w=gradient_ascent(df_math, X_demean, initial_w,eta)

plt.scatter(X_demean[:,0], X_demean[:,1])
plt.plot([0,w[0]*50],[0,w[1]*50],color='red')
plt.show()

③课程思考

---

• PCA在降维之后会天然地具有降噪地作用，假如PCA之后准确率提升，那么就说明元数据有噪点地影响
• 值得一提的是PCA在我这篇文章中使用的是机器学习中搜索的方法，找最大方差，而数学中有专门的公式可以一下子找到所有轴的方向，但是数学有点复杂，等以后再去接触。
• PCA十分地复杂，但是写一篇文章捋捋清楚，对我思路很有帮助。

④课程截图