现在通过一个综合实例,完整地讲述模型的评估与选择。
数据介绍
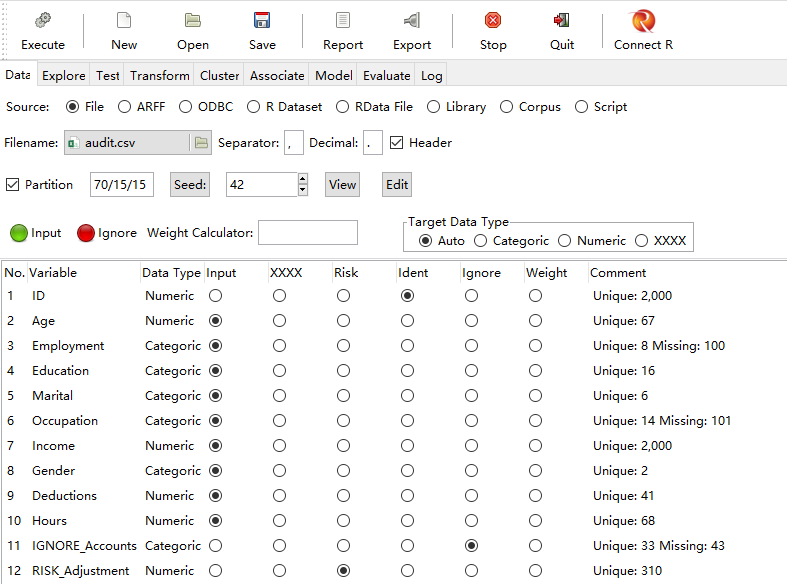
这个案例选择的数据来源于Rattle程序包中关于审计的"audit.csv"数据集,在data选项中,单击“Execute”,这时会弹出是否加载默认数据集的提示,点击“是”,然后在“Filename”中选择“audit.csv”文件,再单击“Execute”,这时就将审计的数据集加载进来了。
读入数据后,切换至Explore选项,对数据集进行描述性分析,选择“Summary”类型,单击“Execute”。
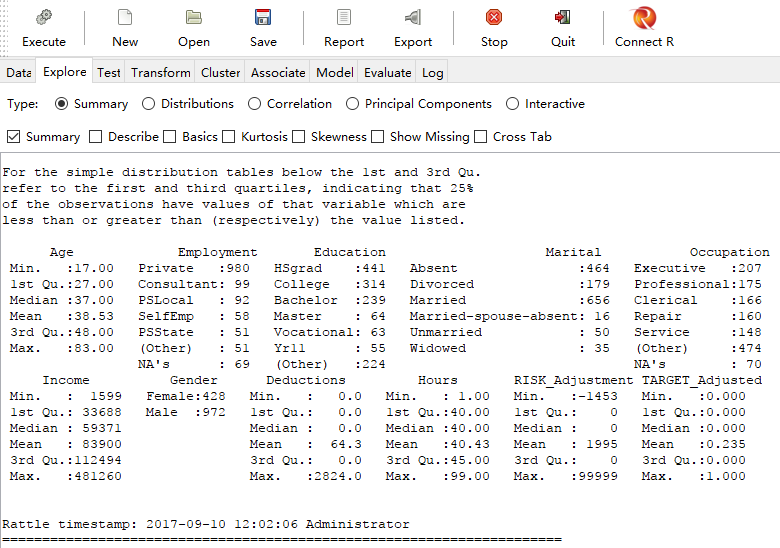
执行结果列出了数据集中所包含的变量,以及变量的最小值、最大值、中位数、众数、均值、四分位数,对于定性变来那个,描述分析图中列出了每个类别的数量。
模型建立
对数据进行了简单分析之后,我们切换至Model选项,选择Forest建立随机森林模型,选择参数,建立500棵决策树,每一节点上利用的大专变量个数为3个,单击“Execute”。
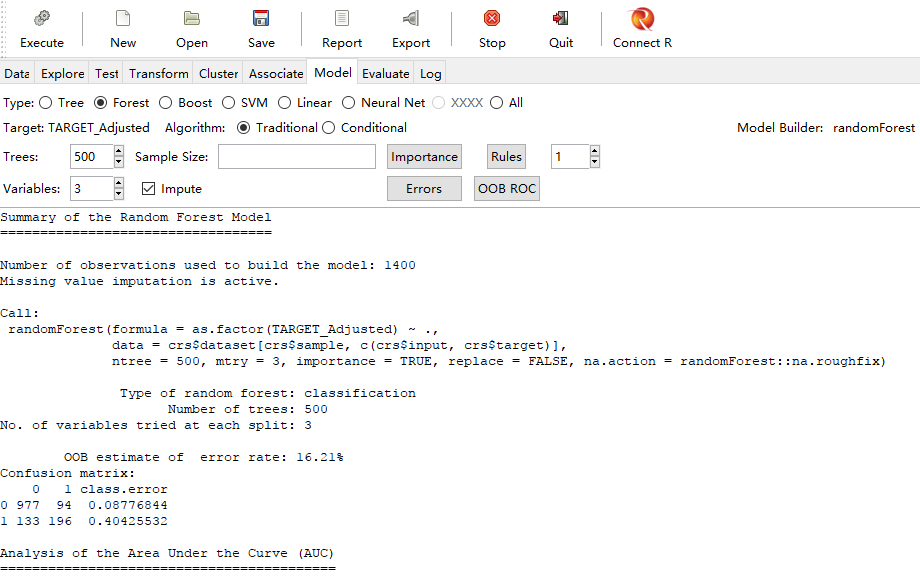
从执行结果我们可以看到,随机森林模型中含有1400个训练集样本,并利用随机森林模型原理对缺失值进行插值。模型利用数据集中的TARGET-Adjusted为响应变量。
模型结果分析
对随机森林模型的结果分析,主要有随机森林的重要值分析、模型之间的混淆矩阵对比分析和模型之间的风险图分析。
1、随机森林重要值分析
随机森林方法的一个重要特征是能够计算每个变量的重要值,Rattle提供两种基本的重要值,一种是采用精度平均减少值作为度量标准,另一种是采用节点不纯度的平均减少值作为度量标准。模型变量重要值的结果分析如下图:
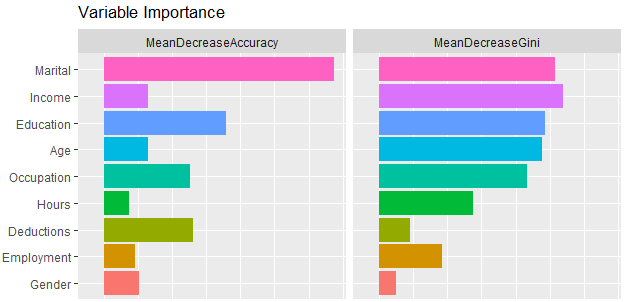
按照第一种标准(MeanDecreaseAccuracy)分析,自变量Marital对于模型的预测能力是最重要的,自变量Income在第一种标准下仅仅属于中等重要程度。然而在第二种判断标准(MeanDecreaseGini)下,自变量Income对于模型的预测能力时非常重要的,而自变量Marital的重要性仅排在第二位。
2、不同模型之间的混淆矩阵对比情况
模型之间的混淆矩阵对比如下图所示:
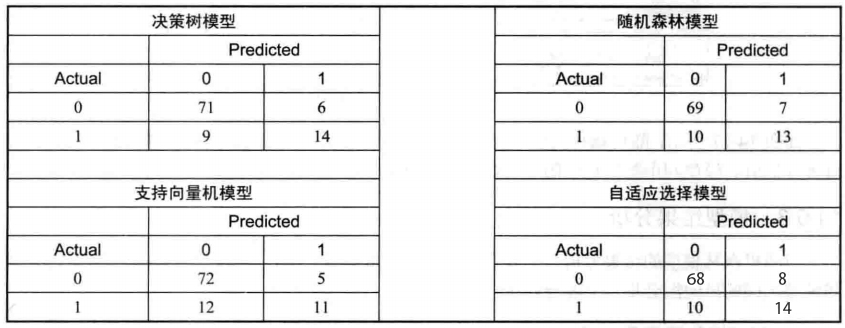
从上图中可以知道:
决策树模型的预测误差为(6+9)/(71+6+9+14)=15%,即将6%的真实结果为0的样本错误地预测为1的类别,将9%的真实结果为1的样本错误地预测为0的类别;
随机森林模型的预测误差为17%,即将7%的真实结果为0的样本错误地预测为1的类别,将10%的真实结果为1的样本错误地预测为0的类别;
支持向量机模型的预测误差为17%,即将5%的真实结果为0的样本错误地预测为1的类别,将12%的真实结果为1的样本错误地预测为0的类别;
自适应选择模型的预测误差为18%,即将8%的真实结果为0的样本错误地预测为1的类别,将10%的真实结果为1的样本错误地预测为0的类别。
单纯从预测模型的混淆矩阵进行分析可以发现,自适应选择模型的预测能力最差,误差高达18%,支持向量机模型以及随机森林模型其次,预测误差为17%,而预测能力较强的模型为决策树模型,预测误差为15%。
3、不同模型之间的风险图分析
不同模型之间的风险图分析如下:
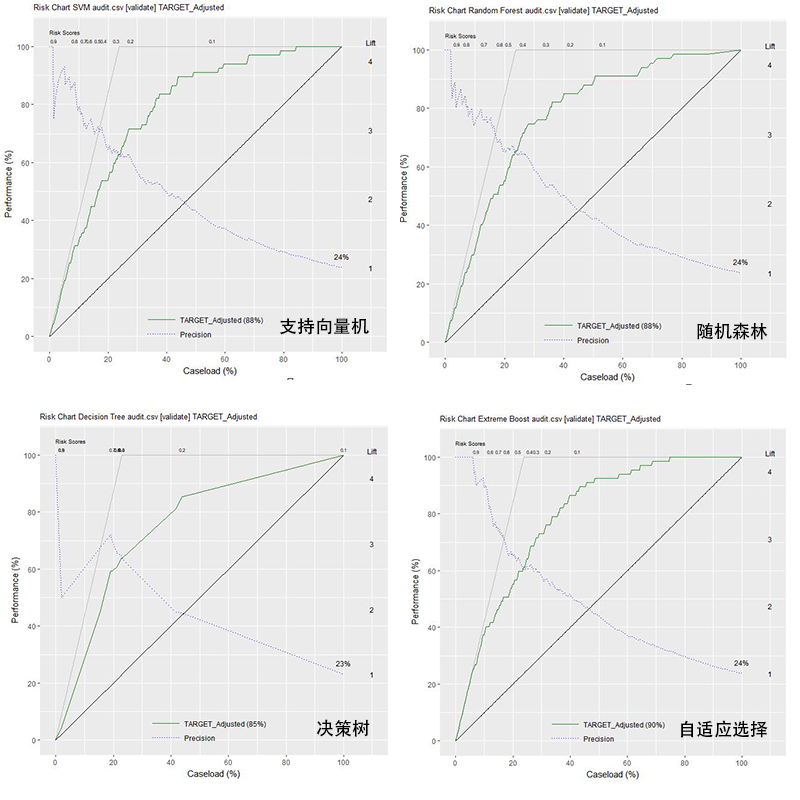
从上图可以得知,图形下方面积最大的是根据自适应选择模型绘制的风险图,该图像中有90%的面积位于Target-Adjusted线的下方,而决策树模型的Target-Adjusted线下方的面积仅为85%,随机森林和支持向量机的线下方面积为88%。
综合分析来看,决策树模型在在混淆矩阵中展现的预测误差率是最低的,预测能力最强,而在风险图分析中,决策树模型的线下方面积所占比最小;与此相反,自适应模型呈现出另一个极端:混淆矩阵中预测能力最差,风险分析中线下面积所占比最大;支持向量机模型与随机森林模型表现中庸。我们暂且先选择随机森林模型来完成下一步的分析操作。
4、模型ROC图及相关图表
模型的ROC图及相关图表如下:
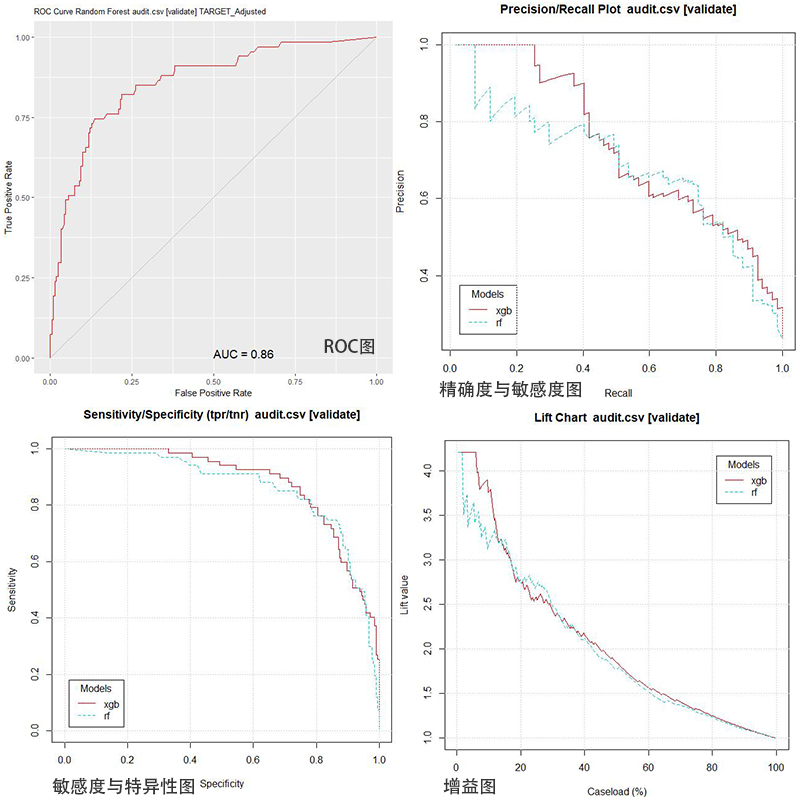
ROC图绘制的是正确肯定判断率与错误肯定判断率之间的关系图。模型正确肯定判断率与错误肯定判断率呈现正比例关系变化,且在错误肯定判断率较低时正确肯定判断率的变化幅度较大;
精确度与敏感度图中,精确度与敏感度呈现反比例变动趋势,说明在获得模型精确度的同时将不得不牺牲模型的敏感度;

 随时随地看视频
随时随地看视频




