学习笔记

记忆化递归

fib

一般实现

const fib = n => {
  if (n === 1 || n === 2) return 1
  return fib(n - 1) + fib(n - 2)
}

console.log(fib(6))
console.log(fib(7))
console.log(fib(8))
console.log(fib(50)) // 卡住了

这样的递归会在每次都计算一次, 造成多次调用多次

优化

我们考虑一下如何优化这个过程

考虑一个简化版的模型, 我们的观察一个这样的函数

当我们递归两次的时候

所以我们之前的fib时间复杂度是

这真是太糟糕了

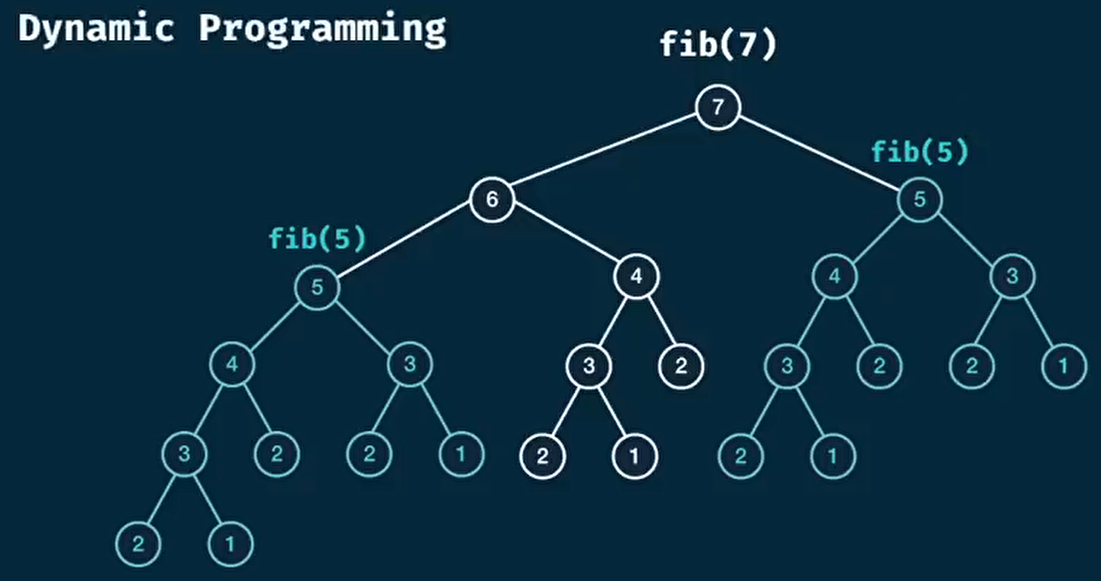
带有记忆的遍历就是dp

// memoization
// js obj, keys: arg, value returns

// 修改1 设置memo和初始值
const fib = (n, memo = {}) => {
  // 修改2 检查是否有记忆
  if (n in memo) return memo[n]
  if (n === 1 || n === 2) return 1
  // 修改3 递归的时候带上我们的引用
  memo[n] = fib(n - 1, memo) + fib(n - 2, memo)
  return memo[n]
}

console.log(fib(6))
console.log(fib(7))
console.log(fib(8))
console.log(fib(50)) // 很快就出结果了

旅行者gridTraveler

我们从极简形式开始分析

其实这也是一种边界情况

简单情况

每移动一步, 问题将会简化

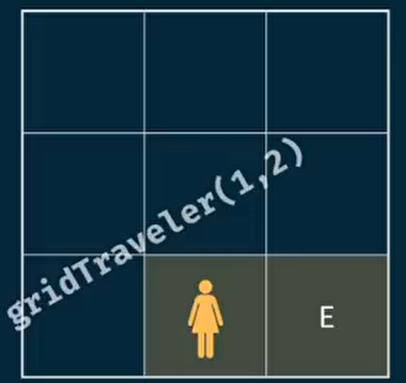
所以我们可以这样想这个问题

具象化的理解就是

递归版

const gridTraveler = (m, n) => {
  if (m === 1 && n === 1) return 1
  if (m === 0 || n === 0) return 0
  return gridTraveler(m - 1, n) + gridTraveler(m, n - 1)
}

console.log(gridTraveler(1,2))
console.log(gridTraveler(3,2))
console.log(gridTraveler(3,3))
console.log(gridTraveler(18,18))

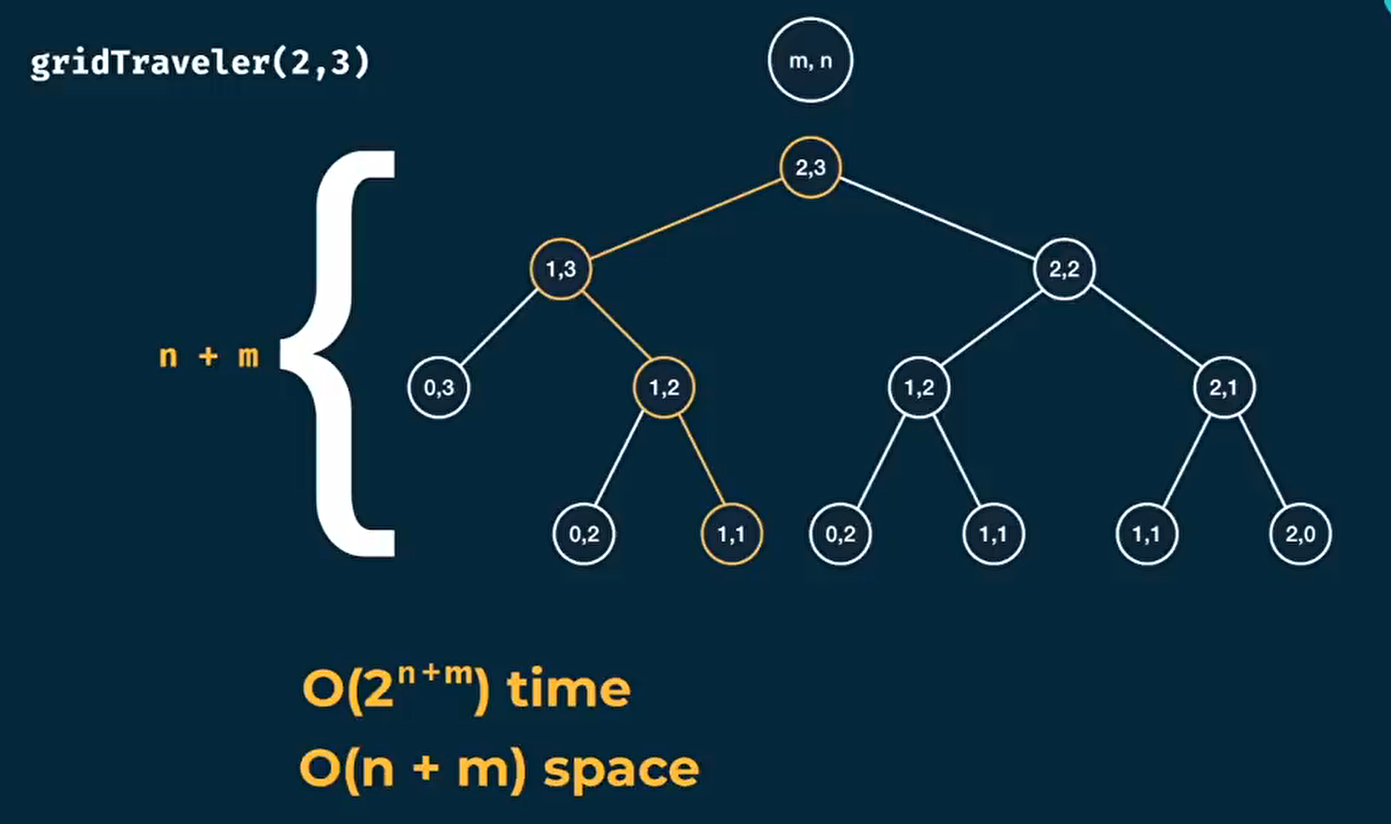
dp版

const gridTraveler = (m, n, memo = {}) => {
  const key = `${m}+${n}`
  if (key in memo) return memo[key]
  if (m === 1 && n === 1) return 1
  if (m === 0 || n === 0) return 0
  memo[key] = gridTraveler(m - 1, n, memo) + gridTraveler(m, n - 1, memo)
  return memo[key]
}

console.log(gridTraveler(1, 2))
console.log(gridTraveler(3, 2))
console.log(gridTraveler(3, 3))
console.log(gridTraveler(18, 18))

这类问题的总结

成功最小结果和失败最小结果

canSum

逆向思维: 求和到定值->使用定值遍历数组减到0

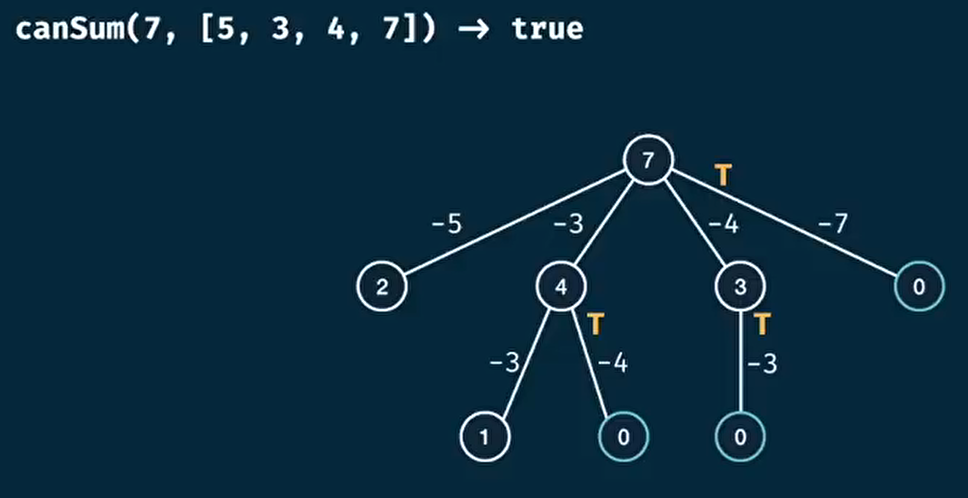
递归

我的解法

const canSum = (targetSum, numbers) => {
  if (targetSum === 0) return true
  if (targetSum < 0) return false

  let remainder
  for (let num of numbers) {
    remainder = remainder || canSum(targetSum - num, numbers)
  }
  return remainder
}

console.log(canSum(7, [3, 2]))
console.log(canSum(7, [4, 2]))
console.log(canSum(7, [5, 6, 2]))
console.log(canSum(300, [7, 14]))

视频解法

const canSum = (targetSum, numbers) => {
  if (targetSum === 0) return true
  if (targetSum < 0) return false

  for (let num of numbers) {
    if (canSum(targetSum - num, numbers)) return true
  }
  return false
}

视频解法递归次数更少

dp

const canSum = (targetSum, numbers, memo = {}) => {
  if (targetSum in memo) return memo[targetSum]
  if (targetSum === 0) return true
  if (targetSum < 0) return false

  for (const num of numbers) {
    memo[targetSum] = canSum(targetSum - num, numbers, memo)
    if (memo[targetSum]) return true
  }
  return false
}

console.log(canSum(7, [3, 2]))
console.log(canSum(7, [4, 2]))
console.log(canSum(7, [5, 6, 2]))
console.log(canSum(300, [7, 14]))

howSum

递归版

const howSum = (targetSum, numbers) => {
  if (targetSum === 0) return []
  if (targetSum < 0) return null

  for (const num of numbers) {
    const remainder = targetSum - num
    const remainderResult = howSum(remainder, numbers)
    if (remainderResult !== null) return [...remainderResult, num]
  }
  return null
}

console.log(howSum(7, [3, 2]))
console.log(howSum(7, [4, 2]))
console.log(howSum(7, [5, 6, 2]))
console.log(howSum(300, [7, 14]))

dp版

const howSum = (targetSum, numbers, memo = {}, path = []) => {
  if (targetSum in memo) return memo[targetSum]
  if (targetSum === 0) return []
  if (targetSum < 0) return null

  for (const num of numbers) {
    const remainder = targetSum - num
    const remainderResult = howSum(remainder, numbers, memo) 
    if (remainderResult !== null) {
      memo[targetSum] = [...remainderResult, num]
      return memo[targetSum]
    }
  }
  memo[targetSum] = null // 不可达也需要记录
  return memo[targetSum]
}

console.log(howSum(7, [3, 2]))
console.log(howSum(7, [4, 2]))
console.log(howSum(7, [4, 3, 2]))
console.log(howSum(7, [5, 6, 2]))
console.log(howSum(300, [7, 14]))

bestSum

tips: 使用递归的思路

想好出口, 边界条件, 失败成功条件
调用递归函数的时候要假设递归函数能获取到你想要的结果

递归版

const bestSum = (targetSum, numbers, lastBest) => {
  if (targetSum === 0) return []
  if (targetSum < 0) return null

  let shortestCombination = null

  for (const num of numbers) {
    const remainder = targetSum - num
    const remainderCombination = bestSum(remainder, numbers)
    if (remainderCombination !== null) {
      const combination = [...remainderCombination, num]
      if (
        shortestCombination === null ||
        combination.length < shortestCombination.length
      )
        shortestCombination = combination
    }
  }

  return shortestCombination
}

console.log(bestSum(7, [1, 3, 2, 7])) // [7]
console.log(bestSum(7, [1, 4, 2])) // [2,4,1]
console.log(bestSum(7, [1, 4, 3, 2])) // [3,4]
console.log(bestSum(7, [1, 5, 6, 2])) // [6, 1]
console.log(bestSum(100, [1, 2, 3, 14]))

dp版

const bestSum = (targetSum, numbers, memo = {}) => {
  if (targetSum in memo) return memo[targetSum]
  if (targetSum === 0) return []
  if (targetSum < 0) return null

  let shortestCombination = null

  for (const num of numbers) {
    const remainder = targetSum - num
    const remainderCombination = bestSum(remainder, numbers, memo)
    if (remainderCombination !== null) {
      const combination = [...remainderCombination, num]
      if (
        shortestCombination === null ||
        combination.length < shortestCombination.length
      )
        shortestCombination = combination
    }
  }

  memo[targetSum] = shortestCombination
  return memo[targetSum]
}

console.log(bestSum(7, [1, 3, 2, 7])) // [7]
console.log(bestSum(7, [1, 4, 2])) // [2,4,1]
console.log(bestSum(7, [1, 4, 3, 2])) // [3,4]
console.log(bestSum(7, [1, 5, 6, 2])) // [6, 1]
console.log(bestSum(100, [1, 2, 3, 5, 10, 40])) //[ 40, 40, 10, 10 ]

这三个问题的总结

canConstruct

很显然, 这和canSum是一类问题

寻找这个问题的边界条件, 也就是递归终止条件, 不断减少字符的长度, 直到为空即可, 失败就是剩余的字符的子字符不在wordbank里面

问题来了1. 如何存储已经匹配的字符? 如何判断当前字符已经不能再被匹配了?

递归版

我的实现(错误版)

每次成功匹配后, 就分割字符串, 依次查询取结果的和运算结果, 当字符串是空为成功结果, 循环完了没有符合条件, 有一个分割后的子串不能满足情况的是失败结果

const canConstruct = (target, wordBank) => {
  if (target === '') return true

  for (const word of wordBank) {
    if (target.indexOf(word) !== -1) {
      return target
        .split(word, 2)
        .reduce(
          (pre, targetStr) => pre && canConstruct(targetStr, wordBank),
          true
        )
    }
  }
  return false
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'Dog', 'Vs']))

仔细想一下, 这个有一个很大的问题, 就是程序匹配到第一个分割点后直接返回, 没有检查第二个分割点是否还能满足条件

console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))// 本该为true, 输出false

所以作出这样的修改

const canConstruct = (target, wordBank) => {
  if (target === '') return true
  return wordBank.reduce((pre, word) => {
    if (target.indexOf(word) !== -1) {
      return (
        pre ||
        target
          .split(word, 2)
          .reduce(
            (pre, targetStr) => pre && canConstruct(targetStr, wordBank),
            true
          )
      )
    }
    return pre
  }, false)
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))

这样就可以解决那个问题了, 但是这样又有一个不太好的地方就是, 不能见好就收, 找到pre是true的时候就可停下来了, 所以, 我们可以使用some来代替, some 在返回true的时候会停止循环, 类似的every将会在返回false的时候跳出循环.

当然还可以使用throw+trycatch完成终止循环, 但是那样太奇怪了, 很反模式, 不过我还是实现了一下

some/every优化版

const canConstruct = (target, wordBank) => {
  if (target === '') return true
  console.log(target, wordBank)
  return wordBank.some(
    word =>
      target.indexOf(word) !== -1 &&
      target.split(word, 2).every(subStr => canConstruct(subStr, wordBank))
  )
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))

try-catch版

看着就恶心

const canConstruct = (target, wordBank) => {
  if (target === '') return true
  try {
    return wordBank.reduce((pre, word) => {
      if (pre === true) throw new Error(true)
      if (target.indexOf(word) !== -1) {
        return (
          pre ||
          target
            .split(word, 2)
            .reduce(
              (pre, targetStr) => pre && canConstruct(targetStr, wordBank),
              true
            )
        )
      }
      return pre
    }, false)
  } catch (e) {
    // console.log(typeof e.message)
    // 注意这里会把boolean转成string, 直接return ture 就好了
    return true
  }
  return false
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))

视频的实现

我们可以从左到右依次检查是否是子串, 这样就可以省很多事情, 而且递归的时候可以不需要检查两边的是否都满足

这体现了一种转换的思路

const canConstruct = (target, wordBank) => {
  if (target === '') return true

  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const suffix = target.slice(word.length)
      if (canConstruct(suffix, wordBank) === true) return true
    }
  }

  return false
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))

之前忘了压力测试的用例了, 不用想, 肯定都跑不完

console.log(
  canConstruct('eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeef', [
    'e',
    'ee',
    'eee',
    'eeee'
  ])
)

我的实现(正确版)

啊这, 过压力测试用例的时候, 发现: 使用split将会把每个e都分割掉, 所以会得到['','']的结果, 所以会错

所以需要实现一个只分割一次的函数

const canConstruct = (target, wordBank) => {
  if (target === '') return true
  return wordBank.some(
    word =>
      target.indexOf(word) !== -1 &&
      splitOnce(target, word).every(subStr => canConstruct(subStr, wordBank))
  )
}

// 只分割一次的函数
const splitOnce = (str, sign) => {
  const index = str.indexOf(sign)
  if (index === -1) return [str]
  return [str.slice(0, index), str.slice(index + sign.length)]
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))
console.log(
  canConstruct('eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeef', [
    'ef',
    'eeeeeeeeeee'
  ])
)
console.log(
  canConstruct('eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeef', [
    'e',
    'ee',
    'eee',
    'eeeeeeeeeee'
  ])
)

dp版

我的实现

const canConstruct = (target, wordBank, memo = {}) => {
  if (target in memo) return memo[target]
  if (target === '') return true
  memo[target] = wordBank.some(
    word =>
      target.indexOf(word) !== -1 &&
      splitOnce(target, word).every(subStr =>
        canConstruct(subStr, wordBank, memo)
      )
  )
  return memo[target]
}

const splitOnce = (str, sign) => {
  const index = str.indexOf(sign)
  if (index === -1) return [str]
  return [str.slice(0, index), str.slice(index + sign.length)]
}

视频实现

const canConstruct = (target, wordBank, memo = {}) => {
  if (target in memo) return memo[target]
  if (target === '') return true

  memo[target] = false
  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const suffix = target.slice(word.length)
      if (canConstruct(suffix, wordBank, memo) === true){
        memo[target] = true
        return true
      }
    }
  }

  return memo[target]
}

countConstruct

递归版

我的实现

const countConstruct = (target, wordBank, counter = 0) => {
  if (target === '') return counter + 1
  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const suffix = target.slice(word.length)
      counter = countConstruct(suffix, wordBank, counter)
    }
  }

  return counter
}

视频实现

const countConstruct = (target, wordBank) => {
  if (target === '') return 1
  let counter = 0
  for (const word of wordBank)
    if (target.indexOf(word) === 0)
      counter += countConstruct(target.slice(word.length), wordBank)

  return counter
}

dp版

const countConstruct = (target, wordBank, memo = {}) => {
  if (target in memo) return memo[target]
  if (target === '') return 1
  let counter = 0
  for (const word of wordBank)
    if (target.indexOf(word) === 0)
      counter += countConstruct(target.slice(word.length), wordBank, memo)

  memo[target] = counter
  return memo[target]
}

我觉得我已经挺熟练了

allConstruct

递归版

我的实现

const allConstruct = (target, wordBank) => {
  const path = []
  helper(target, wordBank, [], path)
  return path
}

const helper = (target, wordBank, currentPath = [], path = []) => {
  if (target === '' && currentPath.length !== 0) {
    path.push([...currentPath])
  }

  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const preCur = [...currentPath] // key: 保存之前的状态, 每次获取子元素的子路径后还回去
      currentPath.push(word)
      helper(target.slice(word.length), wordBank, currentPath, path)
      currentPath = preCur
    }
  }
}

说句实话我也不知道我在写啥

视频实现

const allConstruct = (target, wordBank) => {
  if (target === '') return [[]]

  const result = []

  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const suffix = target.slice(word.length)
      const suffixWays = allConstruct(suffix, wordBank)
      const targetWays = suffixWays.map(way => [word, ...way])
      result.push(...targetWays)
    }
  }

  return result
}

dp版

const allConstruct = (target, wordBank, memo = {}) => {
  if (target in memo) return memo[target]
  if (target === '') return [[]]

  const result = []

  for (const word of wordBank) {
    if (target.indexOf(word) === 0) {
      const suffix = target.slice(word.length)
      const suffixWays = allConstruct(suffix, wordBank, memo)
      const targetWays = suffixWays.map(way => [word, ...way])
      result.push(...targetWays)
    }
  }

  memo[target] = result
  return result
}

列表化tabulation

取消递归, 使用数组记录, 研究每个之前情况对之后情况的影响

fib(nth)

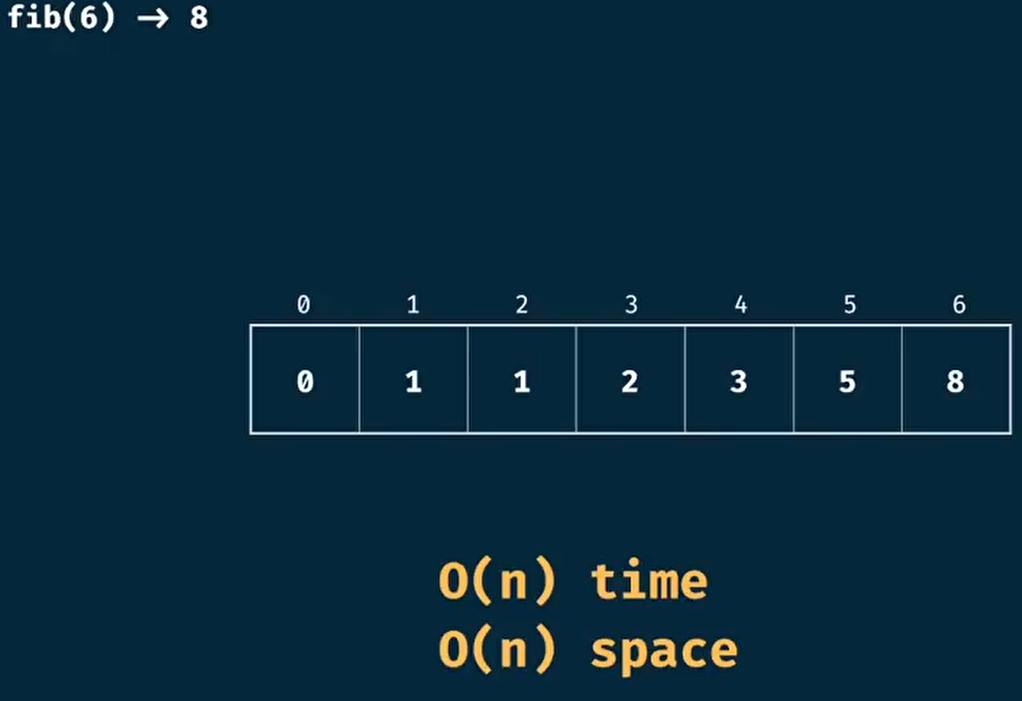
const fib = n => {
  const table = Array(n + 1).fill(0) // 初始化
  table[1] = 1 // 开始, 人工赋值
  for (let i = 0; i < n; i++) {
    // 每个格子会影响后面的两个格子
    table[i + 1] += table[i]
    table[i + 2] += table[i]
  }
  return table[n]
}

console.log(fib(6))
console.log(fib(7))
console.log(fib(8))
console.log(fib(50)) // 很快就出结果了

gridTraveler

const gridTraveler = (m, n) => {
  const table = Array(m + 1)
    .fill() //undefined 不能map
    .map(() => Array(n + 1).fill(0)) //直接full会指向相同的引用

  table[1][1] = 1

  for (let i = 0; i <= m; i++) {
    for (let j = 0; j <= n; j++) {
      if (i + 1 <= m) table[i + 1][j] += table[i][j] // 二维数组左值边界检查
      if (j + 1 <= n) table[i][j + 1] += table[i][j]
    }
  }
  return table[m][n]
}

console.log(gridTraveler(3, 2))

这类问题的总结

规划你的table记录什么
找出你的table的size , 维度
初始化table的值是多少
找到更新table的初值种子 (寻找那个和决定/随机/资源没有关系的情况一般是0/1)
迭代更新table
考察每个格子对未来的格子的影响

canSum

target是0的时候, 一定是true

const canSum = (targetSum, numbers) => {
  const table = Array(targetSum + 1).fill(false)
  table[0] = true
  for (let i = 0; i <= targetSum; i++) {
    if (table[i] === true)
    numbers.forEach(number => {
      table[number + i] = true
    })
  }
  return table[targetSum]
}

console.log(canSum(7, [3, 2]))
console.log(canSum(7, [4, 2]))
console.log(canSum(7, [5, 6, 2]))
console.log(canSum(300, [7, 14]))

小哥陷入无限循环的问题: 不要时刻判断length,这样不好

howSum

const howSum = (targetSum, numbers) => {
  const table = Array(targetSum + 1).fill(null)
  table[0] = []
  for (let i = 0; i <= targetSum; i++) {
    if (table[i] !== null)
      numbers.forEach(number => {
        table[number + i] = [...table[i], number]
      })
  }
  return table[targetSum]
}

console.log(howSum(7, [3, 2]))
console.log(howSum(7, [4, 2]))
console.log(howSum(7, [5, 6, 2]))
console.log(howSum(300, [7, 14]))

bestSum

const bestSum = (targetSum, numbers) => {
  const table = Array(targetSum + 1).fill(null)
  table[0] = []
  for (let i = 0; i <= targetSum; i++) {
    if (table[i] !== null)
      numbers.forEach(number => {
        if (!table[number + i] || table[number + i].length > table[i].length)
          // 如果是null需要给予初值
          table[number + i] = [...table[i], number]
      })
  }
  return table[targetSum]
}

console.log(bestSum(7, [3, 2]))
console.log(bestSum(7, [4, 2]))
console.log(bestSum(7, [5, 6, 2]))
console.log(bestSum(300, [7, 14]))

canConstruct

const canConstruct = (target, wordBank) => {
  const table = Array(target.length + 1).fill(false)
  table[0] = true

  for (let i = 0; i <= target.length; i++) {
    if (table[i] === true)
      wordBank.forEach(word => {
        if (target.slice(i, i + word.length) === word)
          table[i + word.length] = true
      })
  }

  return table[target.length]
}

console.log(canConstruct('', ['cat']))
console.log(canConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(canConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))
console.log(canConstruct('CatVsDog', ['Cat', 'V', 's', 'Dog']))
console.log(
  canConstruct('eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeef', [
    'ef',
    'eeeeeeeeeee'
  ])
)
console.log(
  canConstruct('eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeef', [
    'e',
    'ee',
    'eee',
    'eeeeeeeeeee'
  ])
)

countConstruct

const countSum = (target, wordBank) => {
  const table = Array(target.length + 1).fill(0)
  table[0] = 1

  for (let i = 0; i <= target.length; i++) {
    if (table[i] !== 0)
      wordBank.forEach(word => {
        if (target.slice(i, i + word.length) === word)
          table[i + word.length] += table[i]
      })
  }

  return table[target.length]
}

console.log(countSum('', ['cat']))
console.log(countSum('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(countSum('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(countSum('CatVsDog', ['Cat', 's', 'Do']))
console.log(countSum('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))
console.log(countSum('CatVsDog', ['Cat', 'V', 's', 'Vs', 'Dog']))

allConstruct

const allConstruct = (target, wordBank) => {
  const table = Array(target.length + 1)
    .fill()
    .map(() => [])

  table[0] = [[]]
  for (let i = 0; i < target.length; i++) {
    wordBank.forEach(word => {
      if (target.slice(i, i + word.length) === word) {
        // 对于当前格子的每个情况都需要进行后续单词的检查
        const newCombinations = table[i].map(subArr => [...subArr, word])
        // 增加而不是覆盖
        table[i + word.length].push(...newCombinations)
      }
    })
  }

  return table[target.length]
}

console.log(allConstruct('', ['cat']))
console.log(allConstruct('CatVsDog', ['Cat', 'Vs', 'Dog']))
console.log(allConstruct('CatVsDog', ['at', 'Vs', 'Dog']))
console.log(allConstruct('CatVsDog', ['Cat', 's', 'Do']))
console.log(allConstruct('CatVsDog', ['Cat', 'VsD', 'Vs', 'Dog']))
console.log(allConstruct('CatVsDog', ['Cat', 'V', 's', 'Vs', 'Dog']))

总结

遇见dp问题:

注意到重叠的子问题
决定什么是最小的输入
想一下记忆化递归
想一下列表化问题
画一个策略, 树或者数组

Keep curious, keep learning

【Jeff 在写代码】有关代码的一切的一切

【油管最火的Js动态规划讲解】学习笔记

记忆化递归

fib

一般实现

优化

旅行者gridTraveler

递归版

dp版

这类问题的总结

canSum

递归

dp

howSum

递归版

dp版

bestSum

tips: 使用递归的思路

递归版

dp版

这三个问题的总结

canConstruct

递归版

我的实现(错误版)

视频的实现

我的实现(正确版)

dp版

我的实现

视频实现

countConstruct

递归版

我的实现

视频实现

dp版

allConstruct

递归版

我的实现

视频实现

dp版

列表化tabulation

fib(nth)

gridTraveler

这类问题的总结

canSum

howSum

bestSum

canConstruct

countConstruct

allConstruct

总结