「扫盲」数据结构 - 二叉树入门

🔥 什么是二叉树❔

有一个根节点 🔴 向下扩展两个子节点 🔴 两个子节点又可以向下扩展。类似于这样的结构成为二叉树

上面这种就够就是二叉树，当然有二叉树就有三叉树、四叉树。

树中相应节点的概念

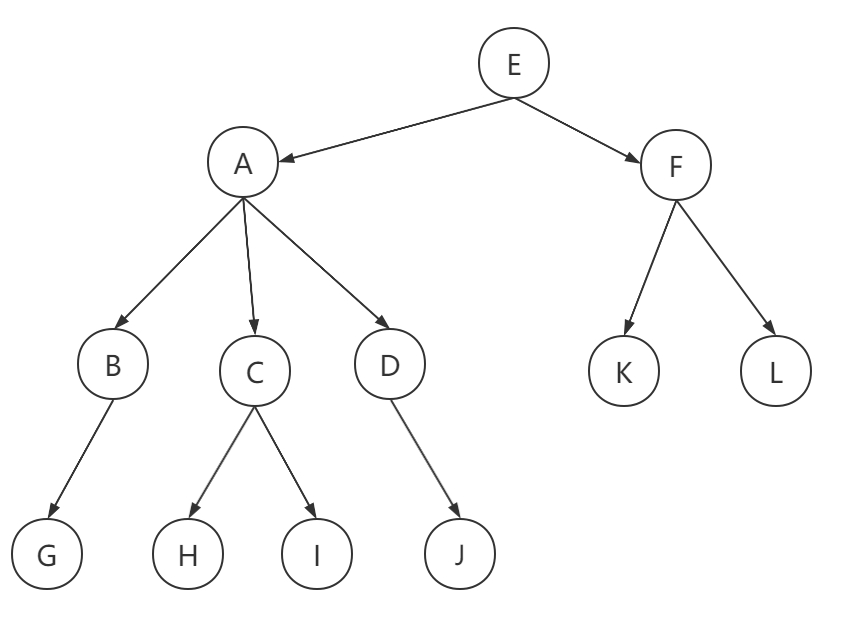
• A 节点是 B 节点的【父节点】
• B 节点是 A 节点的【子节点】
• B、C、D 这三个节点的父亲节点是同一个节点，所以他们之间互称为【兄弟节点】
• E 节点没有父亲节点，所以我们把它称为【根节点】
• G、H、I、J、K、L 没有子节点，所以我们把它称为【叶子节点】
• 节点的高度：节点到叶子节点的最长路径
• 节点的深度：根节点到这个节点所经历的节点个数
• 节点的层数：节点的深度 + 1

二叉树的种类

在二叉树之上，具备各种各样的其他属性，就会衍生出其他的树结构。

• 满二叉树

  

  叶子节点全都在最底层，除叶子节点外，每个节点都有两个子节点，这种二叉树叫做【满二叉树】。

• 完全二叉树

  

  叶子节点都在最底下两层，最后一次的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做【完全二叉树】

• 二分搜索树

  

  若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；

  若任意节点的右子树不为空，则右子树上所有节点的值均大于或等于它的根节点的值；

  任何左子树或右子树也都为二分搜索树。

• 堆

  

  堆就是用数组实现的二叉树，所以它没有使用父指针或子指针。堆根据堆属性来排序。

  堆的常用方法

  构建优先队列、支持堆排序、支持找出一个集合中最小值（或者最大值）

  堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式。

  在最大堆中，父节点的值每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立。

• AVL

• 红黑树

• 线段树

• 字典树

• 并查集

树的遍历

• 前序 根左右

• 中序 左根有

• 后序 左右根

• DFS 深度优先遍历

  代码模板（递归写法）

  visited = set() 
  
  def dfs(node, visited):
      if node in visited: # terminator
      	# already visited 
      	return 
  
  	visited.add(node) 
  
  	# process current node here. 
  	...
  	for next_node in node.children(): 
  		if next_node not in visited: 
  			dfs(next_node, visited)
  

  非递归写法

  def DFS(self, tree): 
  
  	if tree.root is None: 
  		return [] 
  
  	visited, stack = [], [tree.root]
  
  	while stack: 
  		node = stack.pop() 
  		visited.add(node)
  
  		process (node) 
  		nodes = generate_related_nodes(node) 
  		stack.push(nodes) 
  
  	# other processing work 
  	...
  

• BFS 广度优先遍历（层序遍历）

  代码模板

  def BFS(graph, start, end):
      visited = set()
  	queue = [] 
  	queue.append([start]) 
  
  	while queue: 
  		node = queue.pop() 
  		visited.add(node)
  
  		process(node) 
  		nodes = generate_related_nodes(node) 
  		queue.push(nodes)
  
  	# other processing work 
  	...
  

开源项目推荐

[SCHEDULE-BILIBILI]github.com/xiaoxiunique/schedule-bilibili)

只有 Js 能干点啥，JS 和 Github Actions 实现哔哩哔哩每日自动签到、投币、领取奖励。🐄 🍺

[IDEA-TopTips]github.com/xiaoxiunique/tool-tips

IDEA 宇宙最强操作技巧，错误此项目 后悔一生。🐄 🍺