56. 合并区间
题目
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
解题思路
思路:贪心算法
首先需要对题意进行理解(以示例 1,示例 2 为例):
示例 1:
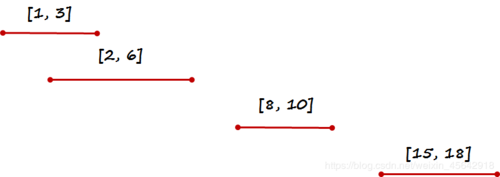
示例 2:
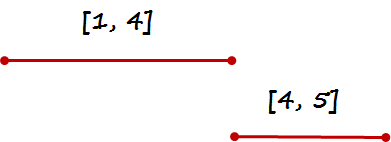
上面示图中,线段比例并非准确的比例,这里仅当做辅助理解。
结合上面的图以及示例输出的结果可看出: 对区间进行合并,那么两个区间之间必然会有交集的部分。再看示例 2,这里交集的部分也可以是一个点。
同样需要注意的地方是: 这里有个前提,就是需要区间要按照左端点进行升序排序。
对给定的列表进行排序后,同时添加结果集,结合两者进行判断是否有交集,从而决定是否要合并区间。
具体的算法:
- 对区间进行排序,以区间左端点为准进行升序排序,然后进行遍历;
- 如果遍历的区间左端点 > 结果集最后一个区间的右端点,那么表示没有交集,这里直接将区间添加到结果集即可;
- 如果遍历的区间左端点 <= 结果集中最后一个区间的右端点,那么说明有交集,这里需要对区间进行合并。具体的做法:对结果集中最后一个区间的右端点进行更新(这里取两个区间的大值)
对于上面产生交集的情况,将最后一个区间的右端点进行更新为最大,达到合并更多区间的结果,这就是贪心策略。
具体实现的代码如下:
代码实现
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
# 对数组进行升序,以数组元素区间左端为准
intervals.sort(key=lambda x: x[0])
# 定义返回数组
ret = []
# 这里合并的依据是区间一定是有交集的
# 即是一个区间左端点 <= 另一个区间右端点
# 反之则没有交集,则不需要合并
# 此时,一个区间的左端点 > 另一个区间的右端点
# 这里主要比较的是排序后的数组区间与返回数组的最后一个区间
for interval in intervals:
# 返回数组为空时,先直接将第一个添加到数组
# 当返回数组不为空时,则根据上面的依据进行区分
# 先看返回数组为空,或者区间没有交集的情况
if not ret or interval[0] > ret[-1][1]:
ret.append(interval)
# 返回数组不为空,有交集的情况,合并区间
# 更新返回数组最后一个区间的右端点,取两区间的大值
else:
ret[-1][1] = max(ret[-1][1], interval[1])
return ret
实现结果
以上就是使用贪心算法的思路,判断区间是否可以合并,需要先对区间进行排序,确定区间之间是否有交集,以此为依据更新结果集,进而解决《56. 合并区间》问题的主要内容。

 随时随地看视频
随时随地看视频




