面试题 01.07. 旋转矩阵
题目
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
解题思路
思路:通过翻转替代旋转
先看示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
题目要求选择旋转 90 度,逐行看旋转之后,每个元素对应的坐标如何变化。
第一行旋转之后的变化:
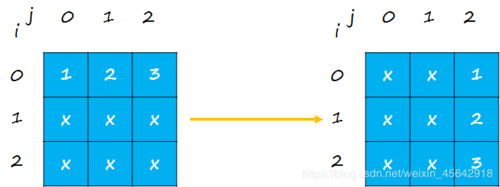
在这里,可以看到,第一行的第 n 个元素,旋转之后变为倒数第一列的第 n 个元素。
第二行旋转之后的变化:
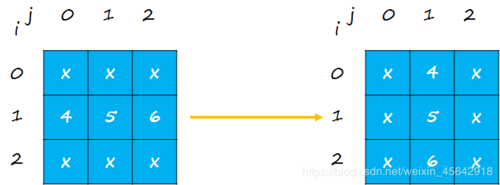
同样,第二行的第 n 个元素,选择之后,是倒数第二列的第 n 个元素。
第三行同理。那么可以得出结论:
原矩阵经过旋转后,原矩阵第 i 行第 j 个元素,将会出现在倒数第 i 列第 j 个位置。
将上面的结论转换成代码,题目明确给出矩阵为 N * N,设矩阵长度为 length,可以表示为:
matrix[row][col] ⇒ matrix[col][length-row-1]
现在,则需要对矩阵进行转换,由上左边式子变为右边式子。本篇运用的是翻转的思路。
假设对原矩阵进行水平翻转,则:
matrix[row][col] ⇒ matrix[length-row-l][col]
假设对原矩阵进行主对角线翻转,则:
matrix[row][col] ⇒ matrix[col][row]
仔细对比前面结论转化的式子,将这两次翻转结合起来,先进行水平翻转,再进行主对角线翻转,则:
matrix[row][col] ⇒ matrix[length-row-1][col]
⇒ matrix[col][length-row-1]
所得出的式子与上面的式子一模一样。
那么就可以按照这个思路,对矩阵进行相应的翻转,得出最终结果。
还有一种翻转的方式,同样可以达到最终效果,如下:
对原矩阵进行主对角线翻转,则:
matrix[row][col] ⇒ matrix[col][row]
对原矩阵进行垂直翻转,则:
matrix[row][col] ⇒ matrix[row][length-col-1]
同样,将两个翻转形式结合起来,先进行主对角线翻转,再进行垂直翻转,可得:
matrix[row][col] ⇒ matrix[col][row]
⇒ matrix[col][length-row-1]
与上面结论中的式子相比,得出的结论同样一致。
具体的代码如下,采用第二种翻转方式。
代码实现
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
length = len(matrix)
# 进行主对角线翻转
for i in range(length):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# 进行垂直翻转
for i in range(length):
for j in range(length // 2):
matrix[i][j], matrix[i][length-j-1] = matrix[i][length-j-1], matrix[i][j]
实现结果
以上就是通过翻转的思想代替旋转,来解决《面试题 01.07. 旋转矩阵》问题的主要内容

 随时随地看视频
随时随地看视频



