面试题62. 圆圈中最后剩下的数字
题目
0,1,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3
输出: 3
示例 2:
输入: n = 10, m = 17
输出: 2
限制:
- 1 <= n <= 10^5
- 1 <= m <= 10^6
解题思路
思路:数学解法。(逆推)
这道题目属于约瑟夫环问题。(有点像丢手绢,摊手)
针对这个题目,先说说难点:
- 数字组成是环形的结构,当数到最后个数字时,还不是需要删除的第 m 个数,需要回至数组的首位继续;
- 每次重新数的位置,都是上次删除数字的下一位。
针对第一个难点,可以考虑取模;
针对第二个难点,可以考虑将删除数字下一位,作为下次重新数的起点,剩余数字依次排列。(注意数字组成是环状的)
考虑先模拟,然后再进行逆推:
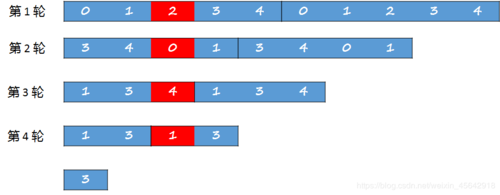
(为体现闭环,这里将数组进行复制。注意: 未得到最后 1 位数时,除第 1 轮开始 ,每一轮都是以上一轮删除数字下一位作为起点,重新数需要删除的第 m 个数)
这就是模拟之后得到的结果。
现在我们来进行逆推:
最终确定的 1 个数字,这个数字对应的索引一定是 0,逆推这个最终数字在每一轮中所处的索引位置,那么假设(n 表示数组元素个数,m 表示要删除的第 m 个数,取示例 1,n = 5, m = 3):
- n = 1 时,索引:0;
- n = 2 时,索引:(0 + m) % 2;
- n = 3 时,索引:((0 + m) % 2 + 3) % 3;
- n = 4 时,索引:(((0 + m) % 2 + 3) % 3 + m) % 4;
- n = 5 时,索引:((((0 + m) % 2 + 3) % 3 + m) % 4 + m) % 5。
大致讲下前面的逆推过程,找出剩余元素在前面每一轮所处的位置:
- 当剩下 1 个数字的时候,这个数字的索引为 0;
- 往前逆推,当剩下 2 个数字的时候,在上一轮元素索引的基础上,要补上 m 个位置,然后对数组元素个数取模,得到这一轮该元素所在的位置,代入 n,m,可得索引为 1;
- 当剩下 3 个数字时,同样补上 m 个位置,然后对数组元素个数取模(这个时候数组元素个数为 3),代入 m,n,得索引为 1;
- …
对上面的逆推过程进行总结:从最后 1 轮往前逆推时,前面一轮的元素所处的位置为,(当前索引 + m) % 前面一轮元素个数。
那么根据这个公式,用代码进行实现。
代码实现
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
ans = 0
# 最后 1 位为最终保留数字
# 往前逆推,从元素个数为 2 开始
for i in range(2, n + 1):
# 逆推公式
ans = (ans + m) % i
return ans
实现结果
以上就是通过数学解法进行逆推,进而解决《面试题62. 圆圈中最后剩下的数字》问题的主要内容。

 随时随地看视频
随时随地看视频




