上一次我们说完了用 HashSet 来进行计数了。我们可以发现,如果我们估计有N个数,那么我们至少需要N*32bit(按照int在32位操作系统下占用32个bit)的空间来进行存储,这太费钱了。有没有办法进行改进呢?这就引出了一个新的数据结构 - BitMap。
这时候看到一张图代表了一个存储int的字节bit信息。
我们可以发现,每一个bit都有自己的值,比如一个int的空间除了作为int类型的数字外,是否还可以做其他的利用?数字可以表示0~31位置的情况,如果我们使用bit的位置信息来存储会怎样?我们来试试看。
如果我们得到Hash的值为0,那就直接将第0位置上的bit位置为1。
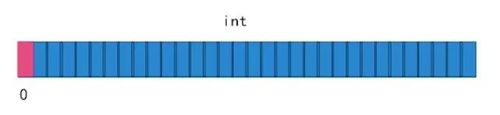
如果我们得到Hash的值为31,那就直接将第31上的bit位置为1。

如果发现位置上已经有值了,那当前的值就已经存在了,不再进行统计,这样子就可以完成超大数据量的统计啦。
这样进行存储的数据结构就叫BitMap,使用每个bit位来进行信息存储,而不是一个int数字。
那有小伙伴就有疑问了,如果超过了32个数字怎么办?可以使用数组来进行拓展,比如一个a = int[2]的数组。
a[0] 可以表示0~31位,a[1] 可以表示32~63位,以此类推,几乎可以无限大。如果数据确实非常巨大,连下标也到达int的界限了,也可以用其他的单个空间更大的数据类型来进行存储。
相比较于HashSet,BitMap 进行统计所使用的存储只需要 HashSet 的1/32。但是这个数据结构简单,相对于 HashSet 有一点小问题,就是hash在数据量巨大的情况下,碰撞会比较严重,那么统计精度会下降,需要怎么改善呢?请关注下一篇布隆过滤器。

 随时随地看视频
随时随地看视频




