Logistic Regression（逻辑回归）是机器学习中一个非常非常常见的模型，在实际生产环境中也常常被使用，是一种经典的分类模型（不是回归模型，不是回归模型，不是。虽然是叫逻辑回归，其实是分类模型。我认为这是因为逻辑回归用了和回归类似的方法来解决了分类问题）。在做分类的时候，很多人都会用逻辑回归先试下，再用复杂的。本文主要介绍了Logistic Regression（逻辑回归）模型的原理以及参数估计、公式推导方法。
模型构建
假设有一个二分类问题，输出为y∈{0,1}，而线性回归模型产生的预测值为z=wx+b是实数值，我们希望有一个理想的阶跃函数来帮我们实现z值到0/1值的转化。然而该阶跃函数是不连续，我们希望有一个单调可微的函数来供我们使用，于是便找到了Sigmoid function来替代。
Sigmoid 函数
公式：
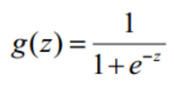
性质：自变量取值为任意实数，值域[0,1]。
解释：将任意的输入映射到了[0,1]区间。我们在线性回归中可以得到一个预测值，再将该值映射到Sigmoid 函数中这样就完成了由值到概率的转换，也就是分类任务。
预测函数：
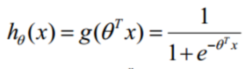
其中
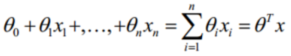
因此对于输入x分类结果为类别1和类别0的概率分别为：
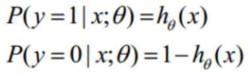
整合：
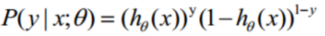
根据上式，接下来我们可以使用概率论中极大似然估计的方法去求解损失函数，取似然函数为：
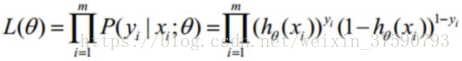
转换为对数似然：
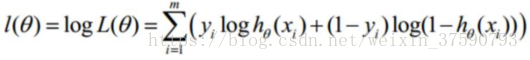
最大似然估计就是要求得使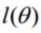
（其里面的
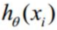和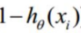
值域为[0,1]所以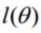是小于0的）取最大值时的 θ ，这里可以使用梯度上升法求解。我们稍微变换一下转换为梯度下降：
求偏导：
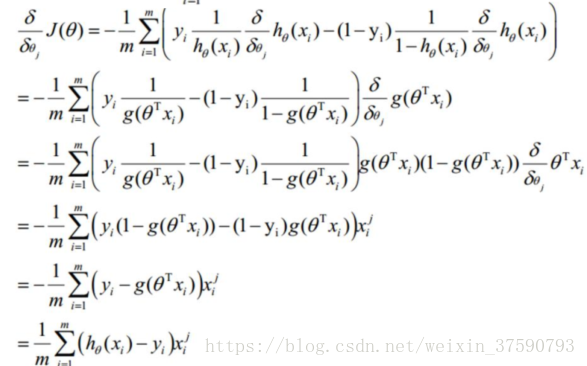
其中i表示第几个样本，j表示第几个特征。
参数更新：
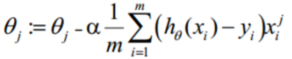
Python代码：
随时随地看视频
