3-玩转数据结构-栈和队列-原创手记-慕课网

我们会介绍两个全新的线性数据结构，栈与队列。

栈Stack

栈也是一种线性结构;相比数组，栈对应的操作是数组的子集;只能从一端添加元素，也只能从一端取出元素(这一端称之为栈顶)

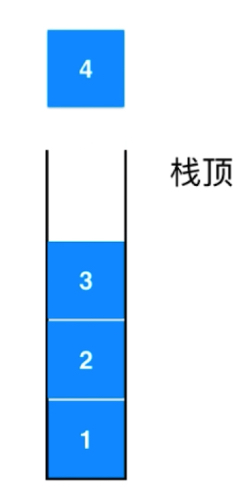
添加元素和取出元素都只能从栈顶位置开始存取。栈是一种后进先出的数据结构。Last ln First Out (LIFO);
在计算机的世界里，栈拥有着不可思议的作用

栈的应用: 无处不在的Undo操作(撤销)

比如你打字: 沉迷学习无法自拔，然后将无法打成不法。

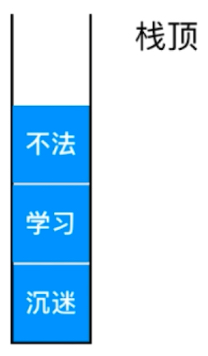
撤销就是将这个不法出栈，然后将后续的正确字都入栈。

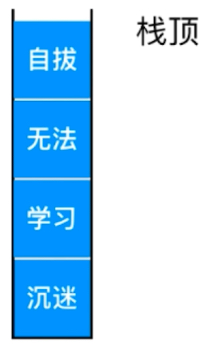
程序调用的系统栈(对于理解递归有作用)

函数A运行到一半，调用函数B; B运行到一半，调用函数C;

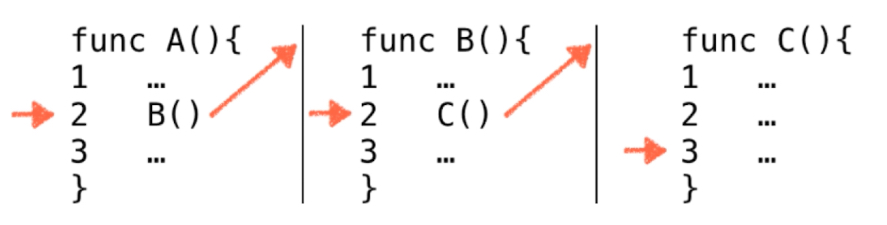
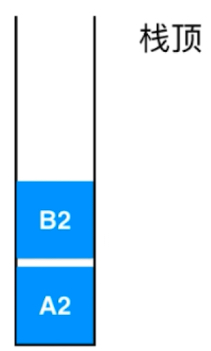
A2指函数A运行到了第二行，B2指函数B运行到了第二行。当函数C顺序执行完毕之后，该执行哪一个函数呢，拿出栈顶B2继续执行。
当B函数执行完毕之后，拿出栈顶A2，执行A函数，执行完之后，发现栈为空，整个程序执行完毕。

子过程，子逻辑的调用，对于理解递归有作用。

栈的实现

Stack<E>void push(E e);      // 向栈中加入元素E pop();           // 弹出栈顶元素E peek( );         // 查看栈顶元素int getSize();     // 获取栈中元素个数boolean isEmpty(); // 判断栈是否为空

从用户的角度看，支持这些操作就好。具体底层实现，用户不关心，实际底层有多种实现方式。

    Interface Stack<E> implement ArrayStack<E>    int getSize();    boolean isEmpty();    void push(E e);    E pop();    E peek();

将我们栈中的常用方法作为一个接口，然后让我们上次实现的动态数组来实现这个接口。

    /**
     * 获取数组最后一个元素(方便我们的栈实现)
     * 
     * @return
     */
    public E getLast(){        return  get(size-1);
    }    /**
     * 获取数组第一个元素
     * 
     * @return
     */
    public E getFirst(){        return get(0);
    }

为Array添加两个方法方便我们的栈实现。

package cn.mtianyan;public class ArrayStack<E> implements Stack<E> {
    Array<E> array;    public ArrayStack(int capacity){
        array = new Array<>(capacity);
    }    public ArrayStack() {
        array = new Array<>();
    }    public int getCapacity(){        return array.getCapacity();
    }    @Override
    public int getSize() {        return array.getSize();
    }    @Override
    public boolean isEmpty() {        return array.isEmpty();
    }    @Override
    public void push(E e) {
        array.addLast(e);
    }    @Override
    public E pop() {        return  array.removeLast();
    }    @Override
    public E peek() {        return array.getLast();
    }    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Stack ：");
        res.append("[ ");        for (int i = 0; i < array.getSize(); i++) {
            res.append(array.get(i));            if (i != array.getSize()-1){
                res.append(", ");
            }
        }
        res.append("] top");        return  res.toString();
    }

}

栈的设计中，用户只关注栈顶元素存取和栈长度。因此不需要提供其他对外方法。

package cn.mtianyan;public class ArrayStackTest {    public static void main(String[] args) {
        ArrayStack<Integer> arrayStack = new ArrayStack<>();        for (int i = 0; i < 5; i++) {
            arrayStack.push(i);
            System.out.println(arrayStack);
        }
        arrayStack.pop();
        System.out.println(arrayStack);
    }

}

运行结果:

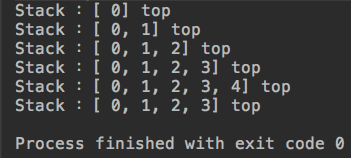
栈的复杂度分析

ArrayStack<E>void push(E e)      // O(1) 均摊E pop()             // O(1) 均摊E peek()            // O(1)int getSize()       // O(1)boolean isEmpty()   // O(1)

这里的push和pop操作在最后面进行，有可能触发resize，但均摊来算是O(1)的。

栈的应用

undo操作-编辑器; 系统调用栈-操作系统;

应用: 括号匹配 - 编译器 LeetCode 问题(leetcode-cn.com) 美版的功能更丰富

https://leetcode-cn.com/problems/valid-parentheses/description/

许多公司真实的面试题。

栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素

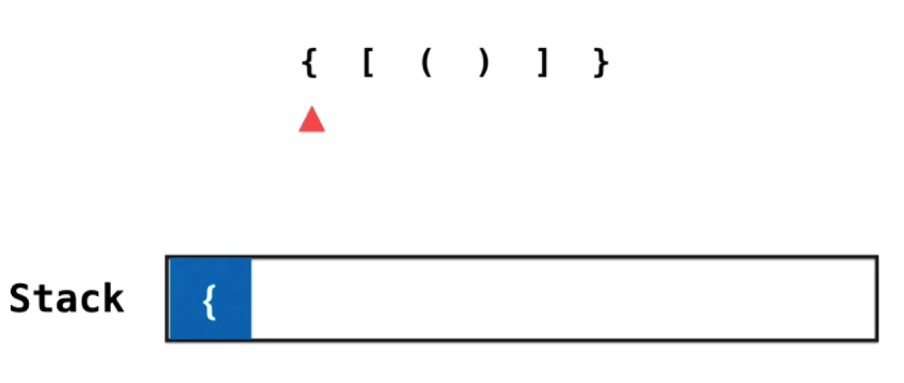
只要是左侧的括号，就压入栈内。

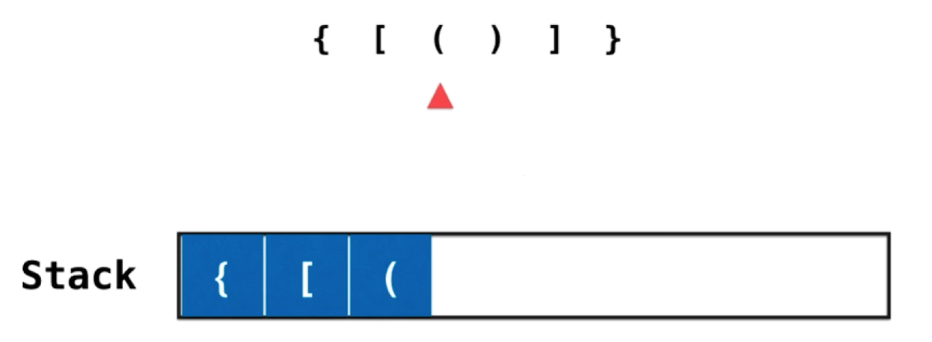
如上图所示，只要是左侧就压入栈。面对字符时右括号，开始查看当前栈顶元素是否可以和该右括号匹配，匹配则出栈。

直到所有字符扫描完毕，栈为空则匹配成功。

失败的例子:

左侧括号全部入栈后，遇到的右括号无法和栈顶匹配,匹配失败。Leetcode会生成相应的语言的答题模板

class Solution {    public boolean isValid(String s) {
        
    }
}

这一小节我们使用import java.util.Stack;,但实际我们自己编写的Stack和java中的这个接口是一致的，下节课教大家在LeetCode用我们自己编写的Stack。

package cn.mtianyan;import java.util.Stack;class Solution {    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();        for (int i = 0; i < s.length(); i++) {            char c = s.charAt(i); // String中的第i个字符
            if (c == '(' || c == '[' || c == '{'){
                stack.push(c);
            }else{                if (stack.isEmpty())                    return false;                char topChar = stack.pop();                if (c ==')' && topChar !='(')                    return false;                if (c ==']' && topChar !='[')                    return false;                if (c=='}' && topChar != '{')                    return false;
            }
        }        return stack.isEmpty();
    }
}

注意topChar时的pop操作，完成了取出栈顶元素和保存栈顶元素两个操作。

附加Python版本实现:

class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = []        for c in s:            if(c=='(' or c=='[' or c=='{'):
                stack.append(c)            else:                if(len(stack) == 0):                    return False
                top_c = stack.pop()                if (c ==')' and top_c != '('):                    return False
                if (c ==']' and top_c !='['):                    return False
                if (c=='}' and top_c != '{'):                    return False
        return len(stack)==0;

if __name__ == '__main__':
    s = Solution()
    print(s.isValid("(]"))

Python版实现要注意list没有push方法，应该使用append方法代替; 注意栈为空(没有待匹配字符直接return False) Python中False是大写，python中获取长度使用len()方法。pop方法还是一样的。

关于LeetCode的更多说明

本地测试,Java版直接添加main函数

public static void main(String[] args) {
        System.out.println(new Solution().isValid("()[]{}"));
        System.out.println(new Solution().isValid("([)]"));
    }

运行结果:

提交时即使添加了main函数也不会报错的。但是请注意不要将自己Package的语句也加入，会报错。

方法必须是public的，因为它会在类外创建自己的Main使用你的方法。

如果我们本地有自己的类接口等，我们可以通过内部类(可以使public也可以是private)来在LeetCode上使用。

class Stack(object):
    """栈"""    def __init__(self):        self.items = []    def is_empty(self):
        """判断是否为空"""
        return self.items == []    def push(self, item):
        """加入元素"""
        self.items.append(item)

    def pop(self):
        """弹出栈顶元素"""
        return self.items.pop()

    def peek(self):
        """返回栈顶元素"""
        return self.items[len(self.items) - 1]

    def size(self):
        """返回栈的大小"""
        return len(self.items)class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = Stack()        for c in s:            if c == '(' or c == '[' or c == '{':
                stack.push(c)            else:                if stack.size() == 0:                    return False
                top_c = stack.pop()                if c == ')' and top_c != '(':                    return False                if c == ']' and top_c != '[':                    return False                if c == '}' and top_c != '{':                    return False        return stack.size() == 0if __name__ == '__main__':
    s = Solution()
    print(s.isValid("(]"))
    print(s.isValid("()"))

Python中不能使用内部类，而是应该该类与class Solution并列。这种提交方式，既可以检验我们的解题，对于我们自己编写的Array Stack也进行检验，值得推荐。

可以看到LeetCode的相关话题。点击可以找到栈相关的题目，可以进行专项练习。

学习方法的疑问:

强烈推荐bobo老师的学习方法指导: https://zhuanlan.zhihu.com/p/35878826

一个课程知识学好几遍，而不是硬扛着一遍强行看完。不懂的先留着，比如我就有一个自己的胡思乱想笔记，记录自己每个阶段遗留问题，日后这些遗留问题在自己学到更深度的知识的时候自然会解决。

这39个问题看看自己感兴趣的，大概了解一下栈能解决什么问题。不是非得把问题做完，才能开始下一节。

不要完美主义。掌握好“度”;学习本着自己的目标去。

对于这个课程，大家的首要目标，是了解各个数据结构的底层实现原理,以及应用。学习到后面，再回头来看。

队列 Queue

队列也是一种线性数据结构; 相比数组，队列对应的操作是数组的子集

只能从一端 (队尾) 添加元素，只能从另一端 (队首) 取出元素

就像一个银行的柜台，从队尾进入元素，在队首有柜台处理，处理了就可以出队。

出队从队首出队，1然后2。

队列是一种先进先出的数据结构(先到先得); First In First Out (FIFO)

Queue<E>void enqueue(E e); // 入队E dequeue();       // 出队E getFront();      // 获取队首元素int getSize();      // 获取队列元素多少boolean isEmpty();  // 是否为空

Interface Queue<E> implement ArrayQueue<E>void enqueue(E e); // 入队E dequeue();       // 出队E getFront();      // 获取队首元素int getSize();      // 获取队列元素多少boolean isEmpty();  // 是否为空

package cn.mtianyan;public interface Queue<E> {    void enqueue(E e); // 入队
    E dequeue();       // 出队
    E getFront();      // 获取队首元素
    int getSize();      // 获取队列元素多少
    boolean isEmpty();  // 是否为空}

package cn.mtianyan;public class ArrayQueue<E> implements Queue<E> {    private Array<E> array;    public ArrayQueue(int capacity) {        this.array = new Array<>(capacity);
    }    public ArrayQueue() {        this.array = new Array<>();
    }    public int getCapacity(){        return array.getCapacity();
    }    @Override
    public void enqueue(E e) {
        array.addLast(e);
    }    @Override
    public E dequeue() {        return array.removeFirst();
    }    /**
     * 获取队首元素
     *
     * @return
     */
    @Override
    public E getFront() {        return array.getFirst();
    }    @Override
    public int getSize() {        return array.getSize();
    }    @Override
    public boolean isEmpty() {        return array.isEmpty();
    }    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Queue ：");
        res.append("front [ ");        for (int i = 0; i < array.getSize(); i++) {
            res.append(array.get(i));            if (i != array.getSize()-1){
                res.append(", ");
            }
        }
        res.append("] tail");        return  res.toString();
    }    public static void main(String[] args) {
        ArrayQueue<Integer> queue = new ArrayQueue<>();        for (int i = 0; i < 5; i++) {
            queue.enqueue(i);
            System.out.println(queue);
        }
        queue.dequeue();
        System.out.println(queue);
    }
}

运行结果:

数组队列的复杂度分析

ArrayQueue<E>void enqueue(E e); // 入队 O(1) 均摊E dequeue();       // 出队 O(n)E getFront();      // 获取队首元素 O(1)int getSize();      // 获取队列元素多少 O(1)boolean isEmpty();  // 是否为空 O(1)

这里入队是从队尾，有可能触发resize，因此均摊下来是O(1)。出队是在队首，数组实现每次都要挪动所有元素,O(n)。

获取队首元素，get(0)，O(1)。剩下两个也是常数级别完成，O(1); 使用循环队列实现即可。

作者：天涯明月笙
链接：https://www.jianshu.com/p/67b262d60bf3