问题内容:
对于平面上给定的N个点,求出所有点对的最短距离,并且标记出这两个点。即,输入是平面上的N个点,输出是N点中具有最短距离的两点。以及其距离。(N大于等于2,0个点或1个点的距离不存在)

算法思想
分治法的解法,就是对于一个规模较大的问题,将其分解为好多个规模较小的子问题,这些子问题的求解不会互相影响,并且与原问题形式相同。 然后递归地去求解解这些子问题,然后将各子问题的解,进行合并,得到原问题的解。
比如,我要在三副装在盒子的乱序扑克里面找到全部的A,问题就可以分解成三个子问题,每个子问题都是一样的,在自己分到的这堆扑克里面找到4张A。然后把这个三个子问题的解合并,就是在三副扑克里面找到全部的A。

求解思路
想要运用分治法,最关键的是找到这个最小的子问题。也就是说,我们不要一下子去想这个大的问题怎么解,我们从0开始,一步步找到一个可以往上拓展进行合并的小规模解。
因为在划分小规模过程中,可能会出现超出题目定义域的情况,因此我们还是从0开始考虑问题。
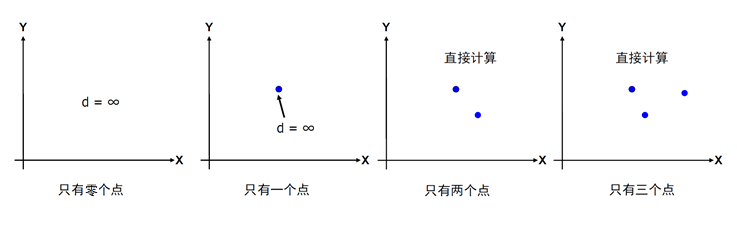
很容易发现,当点数比较少的时候,我们是应该直接进行点的计算的。也就是所谓的穷举,逐个计算两两之间的点距离,找到最小那个就可以的。
取点数为S,当 S<=3 时,可以直接进行求解。
接下来,我们就要考虑当 S>3 时,点数超过3的情况了。
我们的目标是分解大规模问题变成已知的简单小规模问题,因此,很多个点的时候,我们就需要把这些点进行划分,划分成若干个点数比较少的点集,这样就变成上面同样求解的问题了。
那么要如何划分呢? 因为题目中是要求最短距离,所以划分出来的点集肯定是互相靠近的,不然划分出很远的点计算求解出来也是没有意义的。所以我们不妨就从反推的角度,简单的把两个点数小于3的小点集放在一起好了。
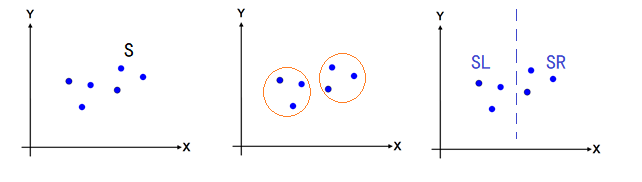
那么我们要把左边这样一堆的点集,划分成右边这样的两个内部互相靠近的小点集,最简单的方法是什么呢? 那当然就是一刀切,找一个位置沿着轴向切一刀,比如这里就可以找到点集合的中点,竖着切一刀,划分成SL和SR两个子点集。
两个递归调用,分别求出SL和SR中的最短距离为dl和dr,再进行比较,取 d=min{dl,dr} 就可以得出一个最短距离了。
看似很完美,那么得到的结果合并的时候会不会有问题呢?
当然有,因为我们只是单独去计算了边界左右两边点集的最小距离,但是对于跨边界的两个点是没有计算过的呀,比如遇到下面这个情况,就会计算得到不准确的结果
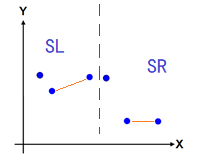
因此,我们还需要去找到跨边界的情况,有没有比当前计算出的左右最小距离更小的情况。既然是要求找更小的,所以我们取当前计算出来两个左右点集最小的距离d, 在直线L两边分别扩展d,得到一个边界区域
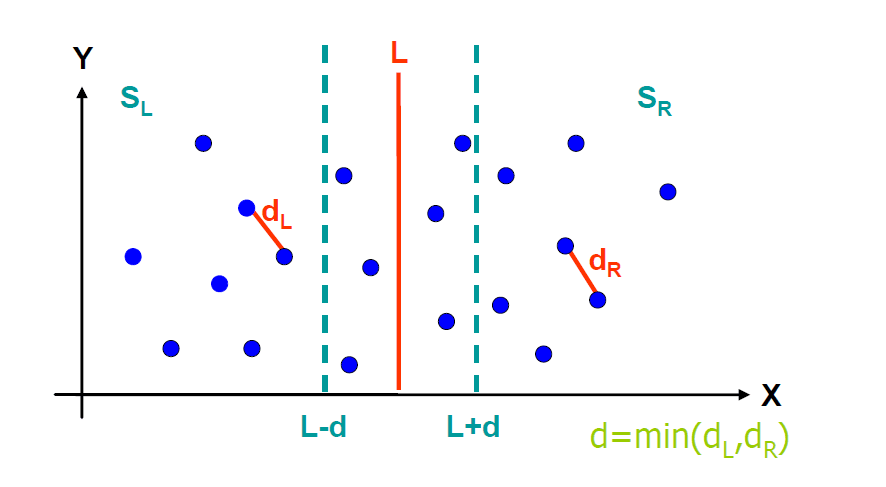
根据已经找到的最小距离d,我们沿着边界mid,分别向左向右开辟一个最小距离d的空间。如果左空间里的某个点,存在连接到右空间更小距离的点,那根据几何原理,这个右空间的点必然落在已左空间某点为圆心,d为半径的一个圆内。
因此,假设左空间的点叫PL,那么对应的右空间的点PR必定满足,在x方向上有 PR[x]<PL[x]+d,在y方向上,PR[y]<PL[y]+d 并且 PR[y]>PL[y]-d , 因为在y方向上,有很明显的排除性,所以可以提前把两个点集按照y方向排序,如果同样y较小的点已经不满足,就不需要再去比较更大的y了。
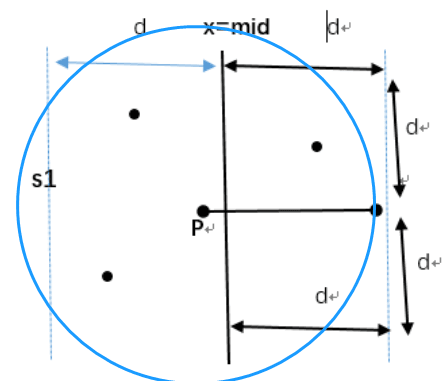
所以,我们再遍历一次在这个圆里的点,如果找到有更小的,我们就修正一下得到的结果值。
因此我们每递归计算出左右两边的最小距离之后,就进行一次这个跨边界的结果修正,一步步就完成全部的计算啦。
具体实现
首先定义点集的数据结构,令点集为一个数组,数组内元素为一个个的点。每个点也用一个数组来表示,第一个元素表示x,第二个元素表示y。x和y默认取值为0到10000。创建对象时,默认生成100个点的点集,生成点集的函数如下。

这个最小距离的线段,是一个对象,里面有两个端点的序号和点本身。(点就是一个数组),以及他们两个点所构成的最短距离。

下面详细说明一下分治法的流程。
首先,需要输入参数作为进行寻找的点集,如果没有,那就默认取对象内自己生成的点集合。
然后对分治法的思维就是,化大为小,使其变成同类型的小规模异界问题。因此我们先来考虑点数少的的情况。
当点的数量小于3的时候,相当于是一个小规模,能够使用最蛮力的方法来进行求解。再细分具体的情况,当数量为0和1,也就是点集切分空或切分只有一个点,这时候是不存在两点之间距离的,我们定义一个很大的长度生成一条无意义line。这样避免对后面找到的小长度段产生影响

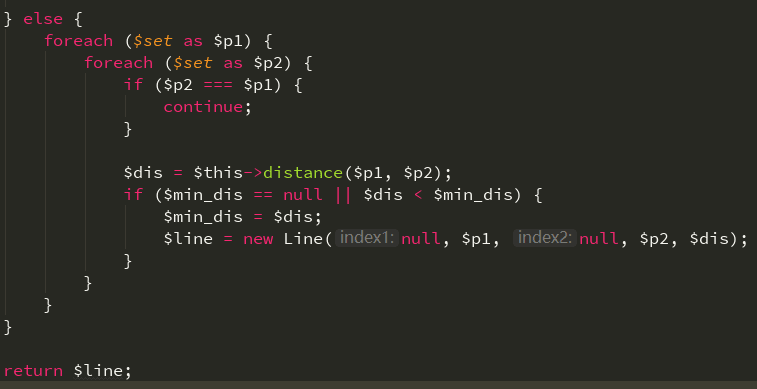
当点集数量大小较小的时候,就直接使用蛮力进行计算即可,遍历点集合求出最小的距离
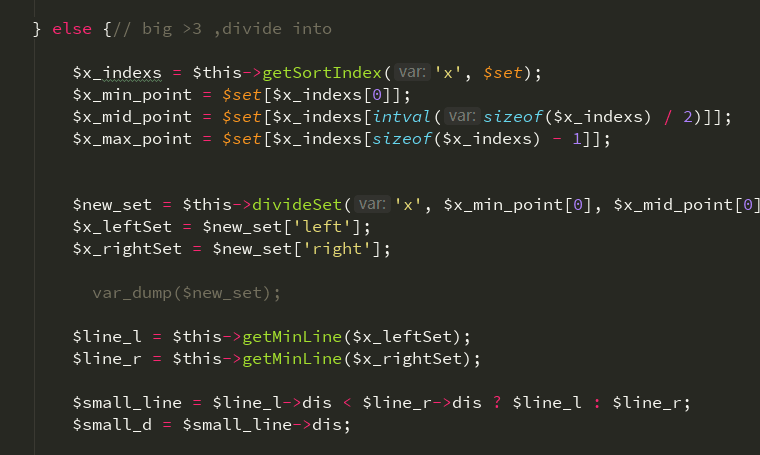
如果点集数量比较大,就需要进行一系列的操作了。为了更方便的获取x方向的中点x mid , 首先根据x进行排序,获取一个点序号的数组,并且用来确定划分点集这个x的范围。
根据点集的变量范围,遍历点集里的点,将其放入不同的数组中进行划分,得到两个更小的点集 leftSet 和 rightSet,并且对两个点集继续递归,划分出更小的点集。
取出两个递归结果中的最小值,也就是初步得到的一个最小距离结果和最小的那个line对象
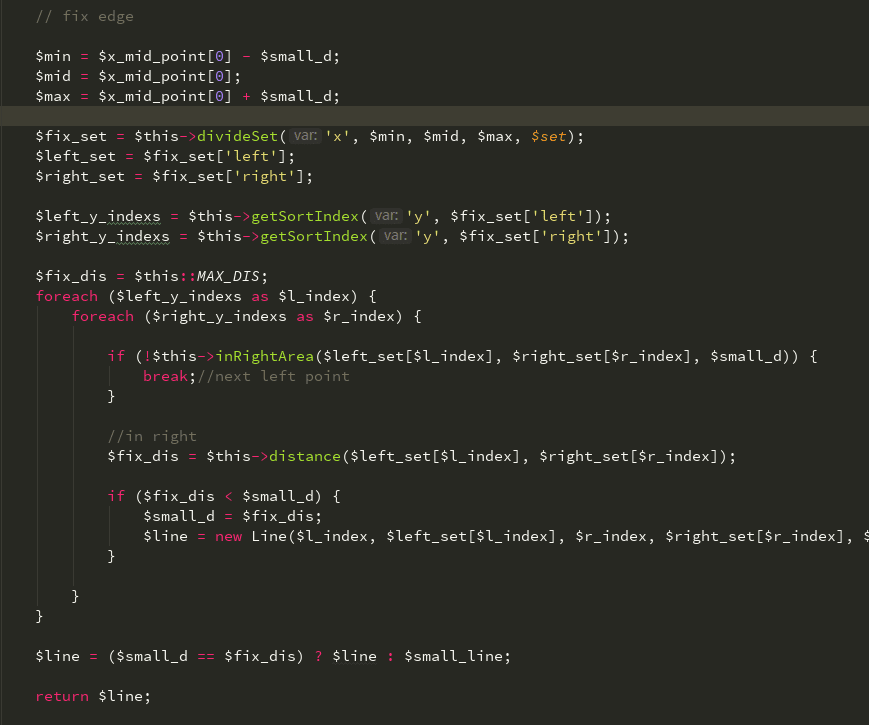
因为这个分治法只是计算了划分区域中的点,对于跨边界的点,每次划分之后还需要做一个单独的修正。
先进行fixset的划分,开辟左右两个区域。因为在y方向上,有很明显的排除性,所以可以提前把两个点集按照y方向排序,如果同样y较小的点已经不满足,就不需要再去比较更大的y了。
对y进行排序得到排序数组。接着从y方向分别遍历两个空间,如果右点不满足条件,就直接break,进行下一个左点的判断。找到更短的距离就进一步更新。最后返回对应的line对象。
由于篇幅所限,图里省略了一些子函数的具体内容太,这里就不贴上全部的代码了。有兴趣的同学可以前往我的Github查看具体的代码。
我把内容封装成了一个 PointSet 类,具体代码请点击右方 【PointSet 类】,查看里面第166行到263行的 public function getMinLine(array $set = null) 函数。




 随时随地看视频
随时随地看视频



