二分搜索树

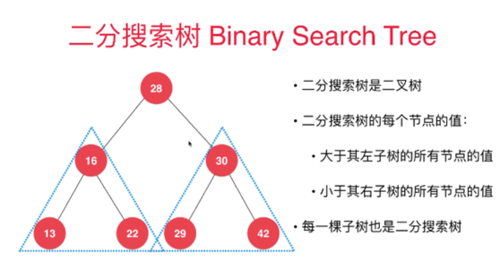
向二分搜索树添加元素

我们把null 也理解为一个数的话，我们就不需要考虑null这个特殊的情况。如果我们插入的node为空，我们插入新元素之后就会产生新的节点，就是new node(e)，之后就是比较。小于0插入左子树，大于0插入右子树。等于0什么都不干，无论向那插入元素，我们都会重新复制左子树和又子树。

public  void add(E e){
   root=add(root,e);
 }
 //递归函数
 private Node add(Node node,E e){
     //首先看递归终止条件
     if(node==null){
         size++;
         return new Node(e);
     }
     //递归调用
     if(e.compareTo(node.e)<0){
        node.left=add(node.left,e);
     }else if (e.compareTo(node.e)>0){
        node.right= add(node.right,e);
     }
     return node;
 }

二分搜索树的前序遍历

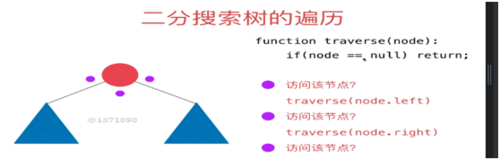
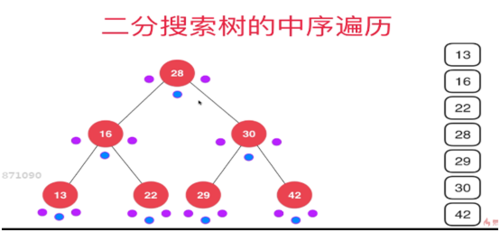
二分搜索树前序遍历的非递归实现

又叫做深度优先遍历-----利用数据结构栈

又称为广度优先遍历----利用数据结构队列

删除而分搜索树的任意元素

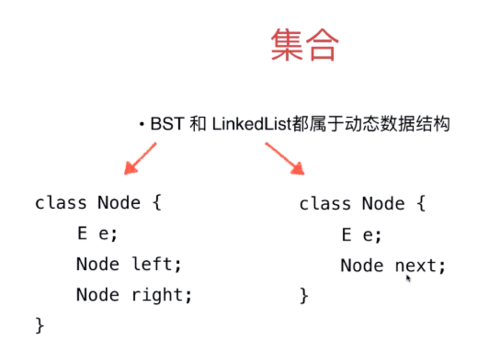
集合基础和基于二分搜索树的集合实现

映射基础（map）

堆

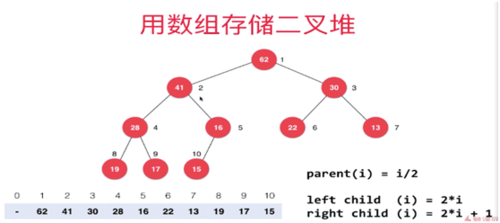
想堆中添加元素和Sift up

首先在数组最后的位置添加一个元素，现在不满足堆定义，所以需要调整，只需要从新添加节点，向上比较就可以了。

从堆中取出元素和sift down

取元素是取堆顶的元素，之后将数组最后一个元素放到堆顶，此时不符合堆的定义，所以要将新放入堆顶元素和他的孩子节点比较（那个大和那个比）

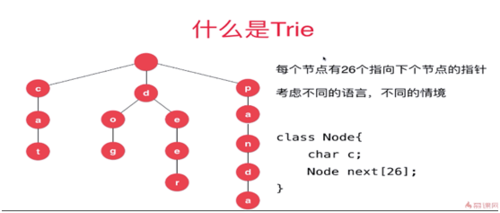
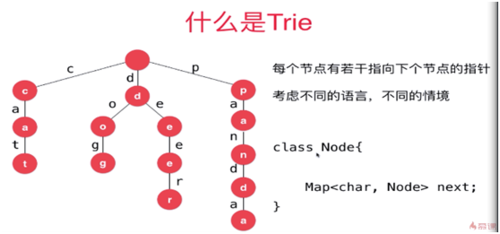
Trie 字典树（多叉树）

平衡树和AVL

标注高度：2节点是叶子节点高度为1 4节点左子树高度为2，3节点高度为3，7节点高度为1.

平衡因子就是左子树高度减右子树高度，2因为是叶子节点，所以平衡因子是0,4节点左子树高度是1，右子树是0 所以平衡因子是1,5节点做子树高度是2，右子树高度是1，所以平衡因子是1.

检查二分搜索树性质和平衡性

旋转操作的基本原理

将相当于将y这个节点顺时针的向右旋转。这样得到新的树既满足二分搜索树又满足平衡树。

左旋转和右旋转的实现

LR和RL

从AVL树中删除元素

// 删除以node为根的二分搜索树中值为e的节点，递归算法
 //返回删除节点删除后新的二分搜索树的根
 private Node remove(Node node, K key) {
     //递归到底
     if(node==null){
         return null;
     }
     Node retNode;
     if(key.compareTo(node.key)<0){
         node.left= remove(node.left,key);
         retNode=node;
     }else if (key.compareTo(node.key)>0){
         node.right= remove(node.left,key);
         retNode=node;
     }else {
         if(node.left==null){
             Node rightNode=node.right;
             node.right=null;
             size--;
             retNode=rightNode;
         }
         else if (node.right==null){
             Node leftNode=node.left;
             node.left=null;
             size--;
             retNode=leftNode;
         }else {
             //待删除节点左右子树军不为null
             //找到比待删除节点大的最小节点，级待删除节点右子树的最小节点
             //用这个节点顶替待删除节点的位置
             Node successor=minimun(node.right);
             successor.right=remove(node.right,successor.key);
             successor.left=node.left;
             node.left=node.right=null;
             retNode=successor;
         }
         
     }
     
     if(retNode==null){
         return null;
     }
 
     //更新height  就是1+左右子树最大height值
     retNode.height=1+Math.(getHeight(retNode.left),getHeight(retNode.right));
 
     //计算平衡因子
     int balanceFactor=getBalanceFactor(retNode);
 
     //平衡的维护
     //LL
     if(balanceFactor>1&& getBalanceFactor(retNode.left)>0){//需要进行右选装
         return rightRotate(retNode);
     }
     //RR
     if (balanceFactor<-1&&getBalanceFactor(retNode.right)<=0) //就是右子树比左子树高，并且高度差比一大，对于节点来说 他的右子树平衡因子是小于等于0的（就是向右倾斜）
     {
         return leftRoate(retNode);
     }
     //LR
     if(balanceFactor>1&&getBalanceFactor(retNode.left)<0){
         //对当前节点左孩子进行左旋转
         retNode.left= leftRoate(retNode.left);
         return rightRotate(retNode);
     }
     //RL
     if(balanceFactor<-1&&getBalanceFactor(retNode.right)>0){
         //对当前节点左孩子进行左旋转
         retNode.right= rightRotate(retNode.right);
         return leftRoate(retNode);
     }
     return retNode;
 
 }

红黑树与2-3树

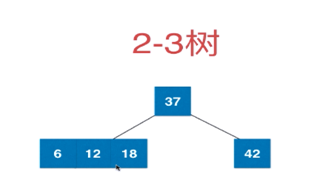
2-3树

树的绝对平衡性

添加节点：从根节点出发添加节点，2-3树添加节点永远不会添加到空的位置。首先添加42节点，再添加37，根据二分搜索树特性，37小于42所以应该添加到左子树中，但是左子树为空，所以新节点应该融合到最后的叶子结点（现在就是42这个节点），42本省是2节点，经过融合变成了3节点，在添加12节点，因为12小于37所以应该添加到37左子树中，但由于左子树为空，所以找最后一个叶子节点融合，12,37,42 此时就变成4节点了，但2-3不存在4节点，所以，此时需要分裂。如下图

此时添加18，从根节点开始，18小于37，所在看左子树，18大于12，所以应该放到12的

右子树中，但右子树为空，所以进行融合，再添加节点6，有需要融合形成4节点，在进行分裂，

如果和根节点分裂一样，那么此时2-3树就不是绝对平衡树，因为根节点到叶子节点的高度不一样了。

为了平衡，我们需要把分裂的非叶子节点向上融合，如下图

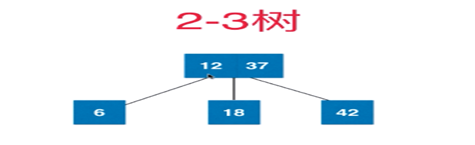
再添加11，添加5

此时出现4节点了所以需要分裂平切向上融合

此时又出现4节点，需要分裂，由于是跟界定所以不用向上融合

红黑树与2-3树的等价

3节点在红黑树中用一条红遍相连表示

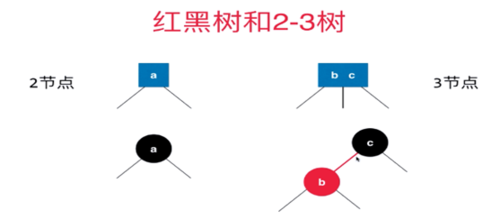
我们没有必要记录那个是红边那个是黑边，由于和父亲节点相连的边只有一条，所以我们把对应的节点表示为红色的。b节点和c节点在原来2-3树中时3节点。

红黑树的基本性质和复杂度分析

保持跟节点为黑色和左旋转

2-3树添加节点永远不会添加到空节点，只会和原有节点融合。

如果融合的节点是2节点，那么直接形成一个3节点

如果融合的节点是3节点，那么也直接融合形成一个4节点，然后在向上分裂。

添加新节点永远是红色的

从最初是情况添加，首先添加42，我们让我们的红黑树的根为42，并且让跟节点变成黑色，

在插入新节点37，根据二分搜索树的规则，需要插入到42的做子树位置，并且是红节点，此时也符合红黑树的定义。

红节点添加到黑节点左侧非常容易，但是根据二分搜索树的原则，新节点有可能添加到二分搜索树的如下图，我们新添加元素在黑节点右侧，现在显然不符合红黑树基本定义（红黑树中所有红节点都是向左倾斜的），所以我们需要左旋转。

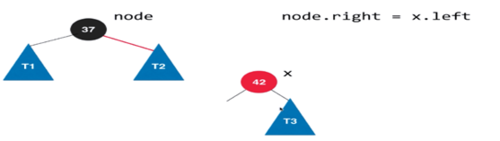
左旋转过程如下图：

首先node的右孩子等于X的左子树，在让X左子树等于node，之后在维护节点颜色，X的颜色等于node的颜色，node的颜色应该为红色。

颜色翻转和右旋转

情况1：

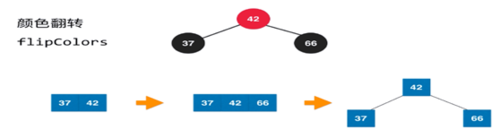
颜色的翻转：我们看添加一个新元素，相当于在2-3树中在3节点添加元素，之后向上分裂，根节点需要向上融合，所以根节点为红色，叶子节点变为黑色。

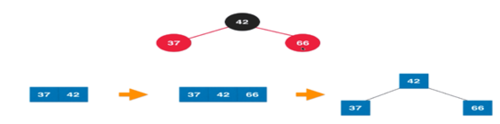
情况2

添加新元素 12 两个红节点在42的左侧，我们现在要实现右旋转，首先42的左孩子指向T1,37的右孩子指向42，在调整相应颜色，37由于代替了原来的42的节点位置，所以37颜色变为原来42的颜色，由于他们还是3节点结构所以42变为红色，在按情况1中进行颜色翻转。

红黑树中添加新元素

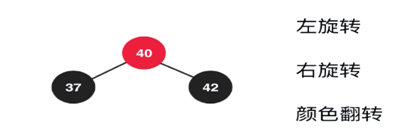
如果出现以下情况，相当于往3节点的中间位置添加元素。

首先基于37这个节点左旋转

在针对42节点在进行右旋转

在进行颜色翻转

情况一

情况2

情况3

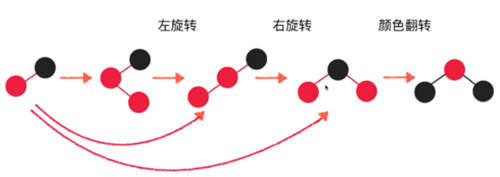
所以红黑树的添加都可以用着一个逻辑链条完成

//返回红黑树根节点，并且为黑色
 public void add(K key,V value) {
     root = add(root, key,value);
     root.color=;
 }
 
 
 
 //递归函数
 private Node add(Node node, K key,V value) {
     //首先看递归终止条件
     if (node == null) {
         size++;
         return new Node(key,value);
     }
     //递归调用
     if (key.compareTo(node.key) < 0) {
         node.left = add(node.left, key,value);
     } else if (key.compareTo(node.key) > 0) {
         node.right = add(node.right, key,value);
     }else {//相等
         node.value=value;
     }
 
     //判断是否需要左旋转
     if(isRed(node.right)&&!isRed(node.left)){
         node=leftRtate(node);
     }
     //判断是否需要右旋转
     if(isRed(node.left)&&isRed(node.left.left)){
         rightRotate(node);
     }
     //判读是否需要颜色翻转
     if (isRed(node.left)&&isRed(node.left)){
         flipColors(node);
     }
     return node;
 }

红黑树的性能测试

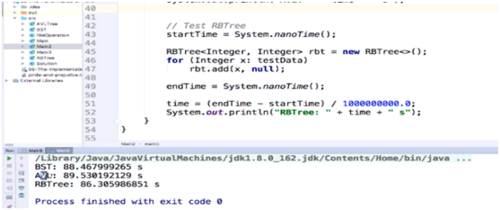
在这个测试用例中红黑树并不是最优，原因有一下几个

1.用例样本数太小，对于比较简单或少的数据，简单算法才是最优

2.红黑树并不是严格的平衡树，从根到叶子节点，高度最多有可能达到2倍的longN,是比AVL树要高一些的，所以在查询操作中红黑树并不占优势，红黑树真正占优势的操作是添加和删除的操作。

我们只看添加操作的测试用例

ConcurrentHashMap（jdk7,基于分段锁处理的）

ConcurrentHashMap 底层结构任然是数组和链表，与HashMap不同的是最外层不是一个大数组而是一个Segment 数组

与hashmap的不同点：

hashmap 线程不安全，如许key和value为空，不容许在遍历的时候修改

ConcurrentHashMap 线程安全不如许key和value为空，如许遍历的时候修改，并且跟新对后面的遍历可见

java8下优化的ConcurrentHashMap 将底层数结构中的链表用了红黑树来提高并发性（默认并发数达到8时将链表变为红黑树）

树结构浅析